ML for Graphs

[!Important] Two different approaches for ML for Graph

  • Feature Engineering

对于不同具体的下游任务，我们都需要重新设计提取特征的策略，层级可能包括 node-level, edge-level, graph-level 等

  • Graph Representation Learning

直接设计算法自动学习图数据的表征特性

Node Embedding

Motivation

我们希望通过 node embedding 将抽象且结构化的图数据中的节点，以特征向量在高维向量空间中表征。为了达到这个目标，我们需要满足以下几点特征:

  • 在高维空间中的嵌入节点应能够显示节点在原图数据中的特征 (如节点间相似性)
  • 能够编码图的信息
  • 在多个下游任务上有良好的表征能力

Framework

对一个 Node Embedding 任务，我们通常可以将其分为以下几个部分:

  • Encoder: 设计编码器架构构建由节点到特征向量的映射
  • 对于节点定义相似函数
  • Decoder: 建立从特征向量到相似度评分的映射
  • 优化 Encoder 参数使得最终嵌入向量良好表征图的性质

Encoder

最简单的 Encoder 算法即为 Shallow Encoder, 我们将每个节点用 one-hot encoding 表示，然后尝试训练一个 Embedding Matrix,其中节点对应的列即为我们要表征的向量

$$ ENC(v) = z_{v} = Z \cdot v $$

$$ Z \in \mathbb{R}^{d \times |V|}, \ v \in I^{|V|} $$

衡量特征向量的相似度

利用两特征向量的点乘大小（即可表征在高维空间中的夹角) 去衡量两特征向量的相似程度

Decoder & Optimization

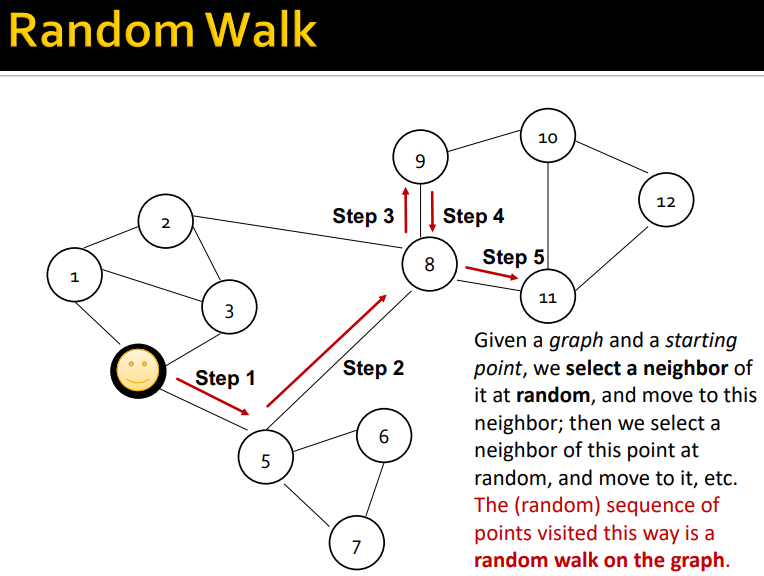
我们利用 Random Walk 来衡量节点间的相似程度

7a455fc058adff2d3a5e399247a1842.png

Random Walk