Basic objects of quantum mechanisms

#PHYS214

Photons

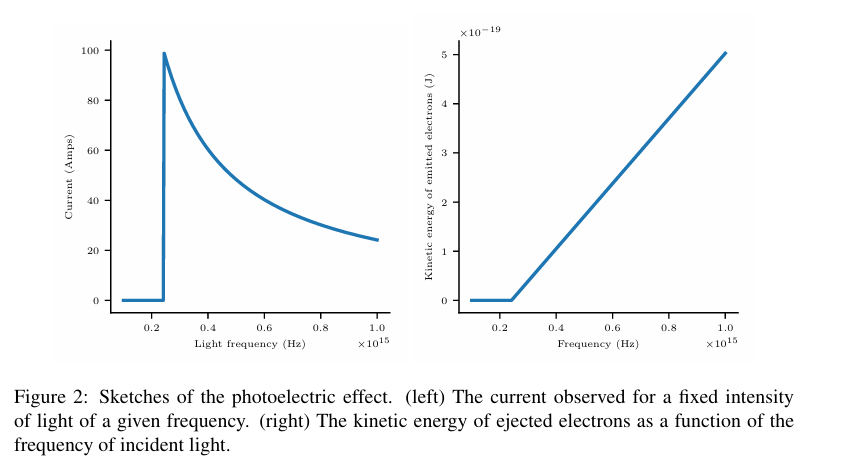
Photoelectric effect 光电效应

光子的能量

$$E=hf$$

光子的动量

$$p=\frac{h}{\lambda }$$

粒子的动能

使电子挣脱金属束缚溢出 ->需达到 threshold

$$E_{initial}=hf-\mathrm{\Phi }\text{ 其中 }\mathrm{\Phi }\text{ 为工作函数}$$

$\mathrm{\Phi }$ 表征材料内部电子的势能

$$E_{final}=K{E}_{electron}$$

• 光强恒定时，输入的光子数量为 $\frac{P}{hf}$ 当频率超过 threshold 后随着频率升高，光子数目减少，激发出的电子数目减少，电流减小
• 电子的动能与光子的频率成线性关系

Relationship between intensity and number of photons

Probability and Complex Numbers

Probability density

$$P(a<x<b)={\int }_a^b\rho (x)dx$$

Normalization Probability:

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\rho (x)dx=1$$

Wave Function

我们利用波函数来描述一个量子系统的状态

Probability density from wave functions

我们将粒子的状态用波函数描述，波函数是一个特定时间下关于位置的函数，其值为复数

$$\rho (x)=|\mathrm{\Phi }(x){|}^2={\mathrm{\Phi }}^{\ast }(x)\mathrm{\Phi }(x)$$

当位置 $a<x<b$ 时，根据上述由波函数推导出的概率函数我们有

$$P(a<x<b)={\int }_a^b\rho (x)dx={\int }_a^b{\mathrm{\Phi }}^{\ast }(x)\mathrm{\Phi }(x)dx$$

在给定的时间下，粒子出现在任何位置的概率均由 wave function 决定

Explaining the two-slit experiment using electrons

Momentum-wavelength relationship

de Brogile wavelength: 德布罗意波长公式
wavefunction 中的 $k$ 与栋梁有如下关系

$$\begin{array}{rlr}& p=\frac{h}{\lambda }& k=\frac{2\pi }{\lambda }\end{array}$$

Normalization of wave functions

波函数的基本性质 ->归一化条件

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{\Phi }}^{\ast }(x)\mathrm{\Phi }(x)dx=1$$

Momentum & Position

Wave Function fo a particle with definite momentum

对于动量确定的粒子，我们用平面波来描述其状态，对应的波函数为：

$$\begin{array}{rlr}& \mathrm{\Psi }(x,t)=A{e}^{i(kx-\omega t)}=A{e}^{i(px-Et)/\tilde{h}}& k=\frac{p}{\hslash },\omega =\frac{E}{\hslash }\end{array}$$

此时其位置在空间中具有一定的概率，我们无法确定其具体位置

$$\rho (x)=|\mathrm{\Psi }(x){|}^2=|A{|}^2$$

Eigenstate

Eigenstate（本征态） 是量子力学中的一个重要概念，它指的是一个量子系统在某个可观测量的测量下，始终会给出确定值的状态。

• 动量本征态（粒子的动量可通过波函数确定）
• 能量本征态（粒子的能量可通过波函数确定）

Superposition of Wave Functions

对于由多确定动量的波函数线性叠加形成的波函数，其观测到的动量并不处于本征态，观测到动量的概率由其线性系数决定

注意：如果波函数公式只出现 sin 或者 cos，记得用欧拉公式进行分解，同时以上系数可以为复数

Heisenberg Uncertainty Principle

海森堡不确定性原理指出：在量子力学中，动量和位置无法同时被精确测量。其数学表达式为：

$$\mathrm{\Delta }x\cdot \mathrm{\Delta }p\ge \frac{\hslash }{2}$$

​

其中：

• $\mathrm{\Delta }x$ 是位置的不确定性（测量时的位置误差）。
• $\mathrm{\Delta }p$ 是动量的不确定性（测量时的动量误差）。
• $\hslash$ 是约化普朗克常数

Energy of Quantum Particles

自由粒子的能量

• 如果粒子具有确定的动量，则其波函数为 $\mathrm{\Psi }(x)=A{e}^{ikx}$。自由粒子的能量由公式 $E=\frac{{\hslash }^2{k}^2}{2m}$ 给出，其中 $k$ 是波函数 $A{e}^{ikx}$ 中的波数。
• 如果测量该粒子的动量（例如，观察它在磁场中的弯曲程度），则动量将以概率 1 出现，结果为 $\hslash k$。可以写成 $p_k=\hslash k$。
• 根据经典力学，自由粒子的能量为 $m{v}^2$。由于公式使用 $p_k=mv=\hslash k$，因此可以将能量写为

$$E_k=\frac{p_k^2}{2m}=\frac{{\hslash }^2{k}^2}{2m}$$

粒子动能计算

基本关系

1. 德布罗意波长 (de Broglie Wavelength) 公式: 物质波的波长 $\lambda$ 与其动量 $p$ 的关系由德布罗意关系给出： $$\lambda =\frac{h}{p}$$ 其中 $h$ 是普朗克常数 (Planck’s constant)，约等于 $6.626\times {10}^{-34}$ J·s。 从这个公式我们可以反解出动量 $p$： $$p=\frac{h}{\lambda }$$

2. 动能 (Kinetic Energy) 与动量 (Momentum) 的关系: 动能 $KE$ 和动量 $p$ 之间的关系取决于粒子是否是相对论性的 (relativistic)，即其速度是否接近光速 $c$。

   • 非相对论情况 (Non-relativistic case): 当粒子的速度 $v$ 远小于光速 $c$ ($v\ll c$) 时，其动能 $KE$ 可以用经典力学公式表示： $$KE=\frac{1}{2}m{v}^2$$ 其中 $m$ 是粒子的质量，$v$ 是其速度。 我们知道动量 $p=mv$，所以 $v=p/m$。代入动能公式： $$KE=\frac{1}{2}m{\left(\frac{p}{m}\right)}^2=\frac{1}{2}m\frac{p^2}{m^2}=\frac{p^2}{2m}$$ 这是非相对论情况下动能和动量的直接关系。

   • 相对论情况 (Relativistic case): 当粒子的速度 $v$ 接近光速 $c$ 时，必须使用相对论的能量-动量关系： $$E^2=(pc{)}^2+(m_0{c}^2{)}^2$$ 其中 $E$ 是总能量 (Total Energy)，$p$ 是动量，$m_0$ 是粒子的静止质量 (rest mass)，$c$ 是光速。 总能量 $E$ 等于动能 $KE$ 加上静止能量 $E_0=m_0{c}^2$： $$E=KE+m_0{c}^2$$ 所以，$KE=E-m_0{c}^2$。将 $E$ 的表达式代入： $$KE=\sqrt{(pc{)}^2+(m_0{c}^2{)}^2}-m_0{c}^2$$ 这是相对论情况下动能和动量的关系。

动量方程

• 对于确定动量的粒子，我们可以用波函数描述粒子的状态，其中动量为 $p$ 的粒子的波函数为 $A{e}^{ikx}$，其中 $k=\frac{p}{\hslash }$。
• 通过将任何波函数扩展为动量本征态的叠加，并读取展开中的概率，可以找到对应动量的可能值与概率。
• 为了找到存在势能时的能量本征态，需要将原理推广到仅仅通过衍射实验测量波函数。量子力学的原理是：通过对波函数进行运算来找到本征态，如果波函数除了总因子外没有改变，那么波函数就是本征态。

动量算子：

$$-i\hslash \frac{\partial }{\partial x}$$

我们将动量算子施加于波函数找到动量

$$-i\hslash \frac{\partial A{e}^{ikx}}{\partial x}=\hslash kA{e}^{ikx}=pA{e}^{ikx}$$

薛定谔方程：能量运算

• 通过与时间无关的薛定谔方程确定哪些波函数是能量本征态。
• 在本部分（以及本课程中），我们只考虑给定时间的波函数，记为 $\mathrm{\Psi }(x)$。对于一维质量为 $m$ 的粒子，薛定谔方程为：

$$-\frac{{\hslash }^2}{2m}\frac{d^2\mathrm{\Psi }(x)}{d{x}^2}+U(x)\mathrm{\Psi }(x)=E\mathrm{\Psi }(x)$$

其中，$U(x)$ 是外部势能，而 $-\frac{{\hslash }^2}{2m}\frac{d^2\mathrm{\Psi }(x)}{d{x}^2}$ 是动量运算的平方，除以 $2m$。这类似于经典力学中将能量写为 $\frac{p^2}{2m}+U$。

方程的要点

• 只有某些波函数满足上述方程 。这些特殊的波函数称为能量本征态。
• $E$ 是一个给出波函数能量的数字。
• 如果粒子处于能量本征态，则对其能量的任何测量都将得到 $E$。对于许多系统，只有某些 $E$ 值具有满足上述方程的波函数。
• 能量本征态被称为静止状态，他们的概率不随时间发生变化

例子：自由粒子

• 描述使用薛定谔方程的自由粒子。在这种情况下，外部势能为零（“自由”的含义！），方程为：

$$ -\frac{\hbar^2}{2m} \frac{d^2 \Psi(x)}{dx^2} = E\Psi(x)

$$

• 最常见的解法是猜测一个波函数，并检查它是否满足方程 5。 假设 ${\mathrm{\Psi }}_k(x)=A{e}^{ikx}$ 是波函数。那么，

$$ -\frac{\hbar^2}{2m} \frac{d^2(Ae^{ikx})}{dx^2} = \frac{\hbar^2 k^2}{2m} \Psi_k(x)

$$

• 如果能量 $E=\frac{{\hslash }^2{k}^2}{2m}$，则此波函数满足薛定谔方程，并且任何这种形式的波函数都是能量本征函数。在这种情况下，$k$ 可以是任何实数，因此能量可以取任何正值。在量子力学中，$k$ 是一个量子数，是能量本征态的标签。
• 这很有意义；之前说过，具有波函数 $e^{ikx}$ 的粒子具有动量 $p=\hslash k$。对于自由粒子，所有能量都是动能，所以期望能量是：

$$ \frac{1}{2} mv^2 = \frac{p^2}{2m} = \frac{\hbar^2 k^2}{2m}

$$

• 因此，导数项与动能相关联，这与势能相关的 $U(x)$ 项相匹配。

例子 II：自由粒子的非能量本征态

• 现在考虑波函数 $\mathrm{\Psi }(x)=a{e}^{i{k}_{1}x}+b{e}^{i{k}_{2}x}$。那么，

$$ -\frac{\hbar^2}{2m} \frac{d^2(ae^{ik_1x} + be^{ik_2x})}{dx^2} = \frac{\hbar^2 k_1^2}{2m} ae^{ik_1x} + \frac{\hbar^2 k_2^2}{2m} be^{ik_2x}

$$

• 无论做什么，都无法在右侧得到 $\mathrm{\Psi }$ 的常数倍，因为 $k_1\ne k_2$。 因此，此波函数不是能量本征态。 事实上，如果使用磁场测量此类粒子的能量，将会测量：

能量	概率
$\frac{{\hslash }^2{k}_1^2}{2m}$	$\frac{a^2}{a^2+b^2}$
$\frac{{\hslash }^2{k}_2^2}{2m}$	$\frac{b^2}{a^2+b^2}$

• 可以计算这个值，因为已经用能量本征态 $e^{i{k}_{1}x}$ 和 $e^{i{k}_{2}x}$ 扩展了 $\mathrm{\Psi }$。

量子化能级：无限深势阱

• 现在考虑 $U$ 不为零的情况。想象创建一个势阱（一维盒子），其中粒子可以从 $x=0$ 到 $x=L$ 自由移动，但在两侧遇到无限势垒。在这种情况下，

$$ U(x) = $$\{\begin{array}{lll}0& \text{如果 }0<x<L\mathrm{\infty }& \text{否则}\end{array}$$

$$

• 回顾方程 4，看看什么样的波函数可以满足等式。 首先注意到，由于盒子外面的 $U$ 为 $\mathrm{\infty }$，因此满足等式的唯一方法是 $\mathrm{\Psi }(x)$ 为零或具有无限能量。 更物理上可能的情况是波函数在盒子外面为零。 从经典上讲，这很有意义； 如果粒子位于具有无限硬壁的盒子内，则在盒子外面找到它的概率为零。
• 在盒子内部，$U=0$，因此薛定谔方程与自由粒子的情况非常相似。 但是，有一个额外的约束 – 波函数在边缘处变为零。 为了满足薛定谔方程，这种情况必须发生，因为那里的势能是无限的。 一个有效的猜测波函数是

$$ \Psi(x) = $$\{\begin{array}{lll}A\sin (\frac{n\pi x}{L})& \text{如果 }0<x<L0& \text{否则}\end{array}$$

$$

• 其中，$n$ 是一个整数。 可以通过强制归一化来找到 $A$：

  $$ \int_0^L A^2 \sin^2(\frac{n\pi x}{L}) dx = 1

$$

• 你可以验证如果 $A=\sqrt{\frac{2}{L}}$，那么这个积分等于 1。 通过将猜测的 $\mathrm{\Psi }$ 代入薛定谔方程，可以得到能量：

$$

E_n = \frac{\hbar^2 \pi^2 n^2}{2mL^2}

$$

重要注意事项：

• 由于边界条件（$\mathrm{\Psi }$ 在 0 和 L 处必须为零），只允许整数 $n$ 值。
• 波函数中的振荡越多，即 n 值越大，能量越高。
• 由于只允许 $n$ 的特定值，因此只允许能量的特定值。

只允许特定能量的含义

• 在前一部分中，看到量子系统有时只能被观察到具有特定的能量值。 实践中理解一下这意味着什么。 假设有一个量子系统（一个原子），它有两个允许的能级 $E_1$ 和 $E_2$，对应的能量本征态为 ${\mathrm{\Psi }}_1$ 和 ${\mathrm{\Psi }}_2$。 可能有更多的能量本征态，但为了简单起见，只考虑这两个。
• 想象一下，原子具有等于基态（最低能态）的波函数 ${\mathrm{\Psi }}_1$。 如果原子没有受到扰动，它将永远保持在基态。 现在假设允许光子靠近原子来扰动系统。 光子有机会与原子相互作用。 让我们考虑一下可能性：
  1. 在此过程结束时，光子发出能量 $\hslash \omega$，原子留下能量 $E_1$。
  2. 光子被原子吸收。 没有光子发出，原子留下能量 $E_2$。
• 虽然可能性 1 总是可能发生的，但只有当 $E_2–E_1=\hslash \omega$ 时，可能性 2 才会发生。 这是因为能量仍然守恒于量子力学中； 因此，如果从 $E_1+\hslash \omega$ 能量开始，当所有事物都解决时，必须以这么多能量结束。 同样，如果原子从 2 开始，那么它可能会发射一个能量为 $\hslash \omega =E_2-E_1$ 的光子。
• 原子、液体、固体等只能吸收能量等于其能级之间差异的光子。 这就是为什么玻璃是透明的，为什么我们可以看穿空气和水。 这就是为什么玫瑰色眼镜会去除除玫瑰色以外的所有颜色。 同样，量子系统只能发射能量等于其能级之间差异的光子。 这就是霓虹灯发出其特定颜色的原因，总的来说，就是赋予物体颜色的原因。 给定量子系统可以获得的能量列表称为光谱。 在拉丁语中，光谱意味着“图像”，实际上量子系统的光谱决定了它与哪种类型的光相互作用。