Waves

#PHYS214

Harmonic Waves

基本形式

沿 x 轴正向传播的单一频率的简谐波，形如：

$$y(x,t)=A\cos (kx-\omega t+\varphi )$$

具体而言，沿 x 轴方向偏振的电磁波可以写为：

$$E_x(x,t)=E_{max}\cos (kx-\omega t+\varphi )$$

相关参数

基本转化

$$\begin{array}{rlrlr}& k=\frac{2\pi }{\lambda }\text{ 描述波在空间上重复的速率}& \omega =2\pi f& T=\frac{1}{f}& v=\frac{\omega }{k}=\lambda f(\mathrm{描}\mathrm{述}\mathrm{波}\mathrm{传}\mathrm{递}\mathrm{的}\mathrm{速}\mathrm{率}，\mathrm{波}\mathrm{长}\mathrm{除}\mathrm{以}\mathrm{周}\mathrm{期})\end{array}$$

振幅与光强：

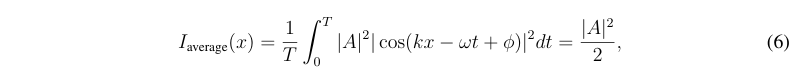
amplitude at a given position and time: $y(x,t)$

Interference

Superposition of waves

相同波长、振幅、波速的波的叠加

$$\begin{array}{rlrl}& y_1(x,t)=A\cos (kx-\omega t+{\varphi }_1)& y_2(x,t)=A\cos (kx-\omega t+{\varphi }_2)& y_{total}(x,t)=y_1(x,t)+y_2(x,t)=2A\cos \left(\frac{{\varphi }_1-{\varphi }_2}{2}\right)\cos (kx-\omega t+\left(\frac{{\varphi }_1+{\varphi }_2}{2}\right))\end{array}$$

相互干涉的波之间的相位差影响平均强度

不同振幅的波的叠加 ->考虑 Phasors 相量图，通过矢量相加

多个不同振幅，不同相位波的叠加:
考虑将每个向量 $A_i\cos ({\varphi }_i)$ 画在向量图中，然后进行矢量相加（可以利用正交分解）

Example

Two speakers
这个例子展示固定相距距离，且两个声源振幅相同叠加的情况

核心还是考虑相位差的来源:
一般为

$$\frac{2\pi }{\lambda }\mathrm{\Delta }r+\mathrm{\Delta }{\varphi }_0$$

Two slits 双缝干涉实验


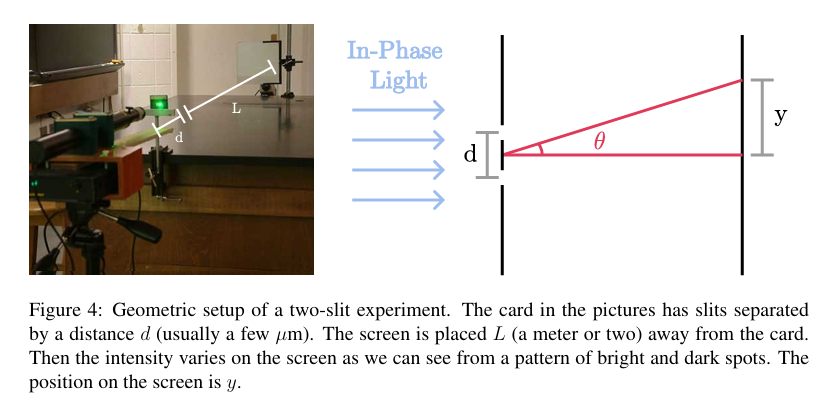
将两缝分别视为独立的波源（波长相同，相位相同，振幅大小取决于缝的宽度），屏幕上不同的光强由不同点到双缝的距离不同导致）

核心影响因素：光程差

$$y_{total}=2A\cos \left(\frac{k\mathrm{\Delta }r}{2}\right)\cos (\frac{k{r}_1+{\varphi }_1+k{r}_2+{\varphi }_2}{2}-\omega t)$$

光程差近似： $\mathrm{\Delta }r=d\sin \theta$
当光程差为波长的整数倍时发生相长干涉；为 $\frac{1}{2}$ 个波长加整数时为相消干涉

$$y_m=L\tan ({\theta }_m)$$

考虑近似 $\theta =\sin \theta =\tan \theta$,可以得到各个亮纹的位置

$$y_m=m\frac{L\lambda }{d}$$

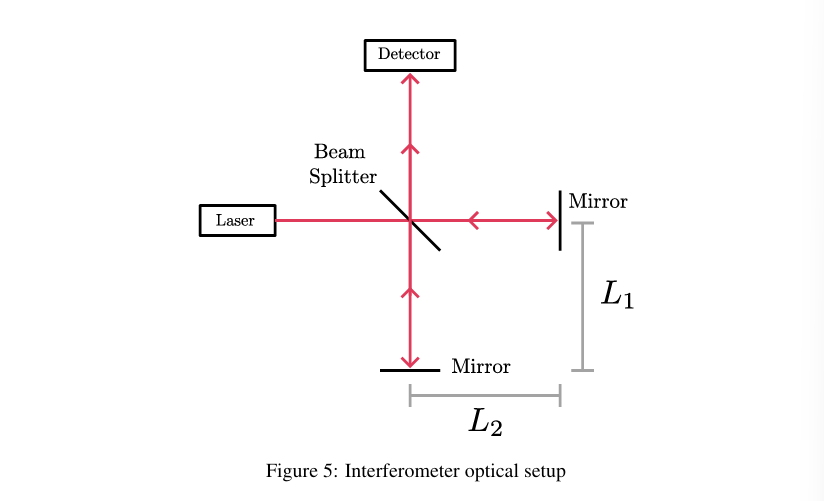
Interferometer 干涉仪

核心因素: 两路径上的光程差,注意为到反射镜距离差的两倍

$$\mathrm{\Delta }r=2(L_1-L_2)$$

$$\mathrm{\Delta }\varphi =\frac{2\pi }{\lambda }\mathrm{\Delta }r=\frac{4\pi }{\lambda }(L_2-L_1)$$

Diffraction 衍射

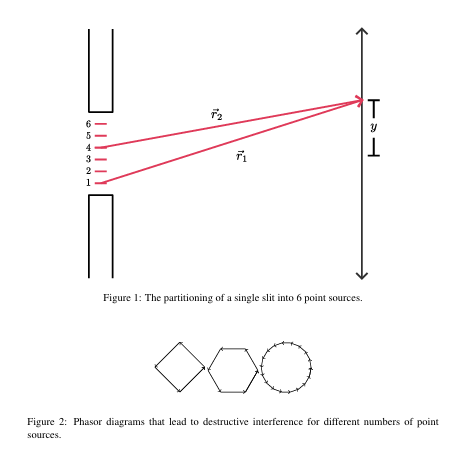
Diffraction from a single slit

先考虑使光强为 0 的角度 ${\theta }_0$ ，确定光斑大小

• 考虑将宽度为 a 单缝建模为由 N 个点光源组成，其中点光源之间的间距为 $d=\frac{a}{N}$ , 考虑 $N\to \mathrm{\infty }$ 的情况
• 然后计算相消干涉 ->即所有的向量相加和为 0->这些向量均匀排布在单位圆上
• 相邻两者相差相位为 $\frac{2\pi }{N}$

$$k(r_2-r_1)=\frac{2\pi }{N}$$

其中 $r_2-r_1=\frac{a}{N}\sin {\theta }_0$,推出

$$a\sin {\theta }_0=\lambda$$

则

$$y_0=L\tan {\theta }_0$$

Diffraction for a circular aperture

推导过程与单缝类似，对于直径为 $D$ 的圆孔，需满足的条件为

$$D\sin {\theta }_0=1.22\lambda$$

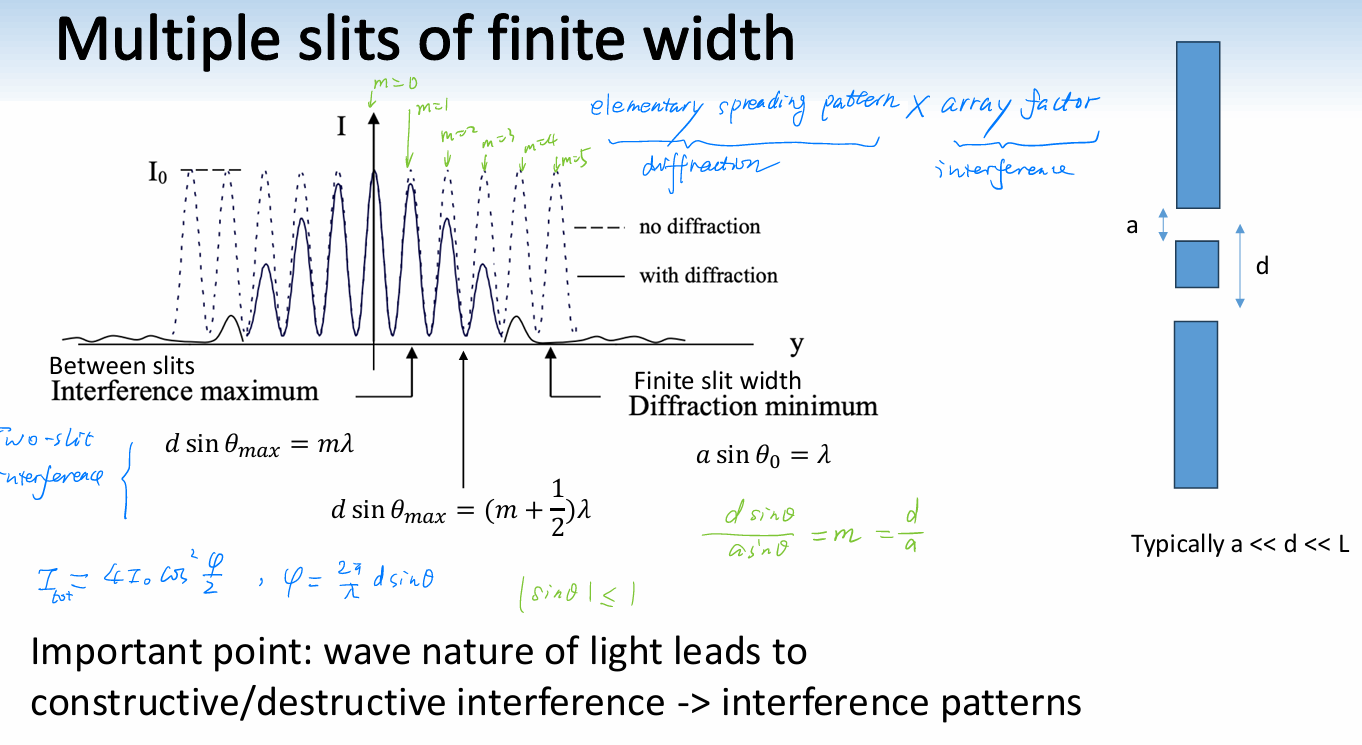
Diffraction from multiple slits

Example: Diffraction and lithography

Lithography Machine 光刻机

一般情况下我们希望衍射光斑尽可能小 ->希望 ${\theta }_0$ 尽可能小,以区分不同的对象
当波长增加时，蚀刻的孔径增大
当透镜直径增大时，蚀刻的孔径减小

计算思路

• 先考虑根据物体到透镜距离以及轨迹长度计算分离角度
• 根据计算出的角度计算圆形孔径

Example: Homework3.4