Thermodynamics out of equilibrium

#PHYS213

Lecture 7: Thermodynamic Processes Reversible Processes

系统状态的变化路径称为热力学过程。我们特别关注以下四种理想化的过程，它们构成了许多热力学循环的基础：

1. 等容过程 (Isochoric Process):
   • 定义：体积 $V$ 保持不变 ($dV=0$)。
   • P-V 图：一条垂直的线段。
   • 热力学第一定律 (First Law of Thermodynamics, FLT): $\mathrm{\Delta }U=Q-W_{by}$。
   • 做功 (Work done by the system): $W_{by}=\int pdV=0$。因为体积不变，系统不对外做功。
   • 热量 (Heat): $Q=\mathrm{\Delta }U$。所有传入的热量都用于增加系统的内能。
   • 对于理想气体 (Ideal Gas): $\mathrm{\Delta }U=C_V\mathrm{\Delta }T=\alpha Nk\mathrm{\Delta }T$。因此 $Q=C_V\mathrm{\Delta }T$。 (这里 $\alpha$ 取决于气体类型，例如单原子气体 $\alpha =3/2$)。利用理想气体状态方程 $pV=NkT$，在体积不变时，$p/T=\text{constant}$，所以 $\mathrm{\Delta }p/\mathrm{\Delta }T=\text{constant}$，可以得到 $\mathrm{\Delta }U=\alpha V\mathrm{\Delta }p$ (如 Slide 8 所示)。
2. 等压过程 (Isobaric Process):
   • 定义：压强 $p$ 保持不变 ($dp=0$)。
   • P-V 图：一条水平的线段。
   • 做功: $W_{by}=\int pdV=p\int dV=p(V_f-V_i)=p\mathrm{\Delta }V$。
   • 内能变化 (Internal Energy Change): $\mathrm{\Delta }U=C_V\mathrm{\Delta }T$ (对于理想气体，内能仅是温度的函数)。
   • 热量: $Q=\mathrm{\Delta }U+W_{by}=C_V\mathrm{\Delta }T+p\mathrm{\Delta }V$。
   • 对于理想气体: $p\mathrm{\Delta }V=Nk\mathrm{\Delta }T$。所以 $Q=C_V\mathrm{\Delta }T+Nk\mathrm{\Delta }T=(C_V+Nk)\mathrm{\Delta }T$。我们定义 定压热容 (Heat capacity at constant pressure) $C_p=C_V+Nk$。因此 $Q=C_p\mathrm{\Delta }T$。
   • 技术比喻: 等压加热时，系统像一个需要推开活塞才能膨胀的气球。一部分热量用来提高内部温度（增加内能 $\mathrm{\Delta }U$），另一部分则用来对外做功 $W_{by}$ 把活塞推开。因此，等压过程比等容过程需要更多的热量来达到相同的温度升高，即 $C_p>C_V$ (Slide 5)。
3. 等温过程 (Isothermal Process):
   • 定义：温度 $T$ 保持不变 ($dT=0$)。
   • P-V 图：一条双曲线 ($p\propto 1/V$ 对于理想气体)。
   • 对于理想气体: 内能 $U$ 只依赖于 $T$，所以 $\mathrm{\Delta }U=0$。
   • 热力学第一定律: $\mathrm{\Delta }U=0=Q-W_{by}$，因此 $Q=W_{by}$。系统吸收的热量全部用来对外做功。
   • 做功 (理想气体): $$W_{by}={\int }_{V_i}^{V_f}pdV={\int }_{V_i}^{V_f}\frac{NkT}{V}dV=NkT{\int }_{V_i}^{V_f}\frac{dV}{V}=NkT\ln \left(\frac{V_f}{V_i}\right)$$
   • 这个过程通常需要系统与一个大的 热库 (thermal reservoir) 接触以保持温度恒定。
4. 绝热过程 (Adiabatic Process):
   • 定义：系统与外界没有热量交换 ($Q=0$)。这通常发生在快速进行的过程中（来不及热交换）或者系统被良好绝热时。
   • P-V 图：比等温线更陡峭的曲线。
   • 热力学第一定律: $\mathrm{\Delta }U=Q-W_{by}=-W_{by}$。系统对外做功会导致内能减少（温度下降），对系统做功会导致内能增加（温度升高）。
   • 对于理想气体 (准静态过程 Quasi-static process): 我们可以推导出过程方程 (Slide 6)。从 $\mathrm{\Delta }U=-W_{by}$ 开始： $\alpha NkdT=-pdV=-\frac{NkT}{V}dV$ 分离变量：$\alpha \frac{dT}{T}=-\frac{dV}{V}$ 积分：$\alpha \int \frac{dT}{T}=-\int \frac{dV}{V}$ $\alpha \ln T=-\ln V+\text{constant}$ $\ln (T^{\alpha })+\ln V=\text{constant}\Rightarrow \ln (T^{\alpha }V)=\text{constant}$ 所以: $$T^{\alpha }V=\text{constant}$$ 利用 $pV=NkT$ 消去 $T$ ($T\propto pV$)，得到： $(pV{)}^{\alpha }V=\text{constant}\Rightarrow p^{\alpha }{V}^{\alpha +1}=\text{constant}$ 两边取 $1/\alpha$ 次方: $p{V}^{(\alpha +1)/\alpha }=\text{constant}$。 我们定义 绝热指数 (adiabatic index) $\gamma =C_p/C_V=(C_V+Nk)/C_V=(\alpha Nk+Nk)/(\alpha Nk)=(\alpha +1)/\alpha$。 因此，理想气体准静态绝热过程满足： $$p{V}^{\gamma }=\text{constant}$$ 因为 $\gamma =(\alpha +1)/\alpha >1$，所以绝热线 $p\propto V^{-\gamma }$ 比等温线 $p\propto V^{-1}$ 更陡峭 (Slide 7)。

可逆性与不可逆性 (Reversibility and Irreversibility)

(Slide 10-14, 26)

• 可逆过程 (Reversible Process): 一个过程是可逆的，如果它可以通过无穷小的改变，使得系统和环境都精确地回到初始状态，并且不留下任何其他变化。
  • 关键特征：过程进行得无限缓慢 (准静态，quasi-static)，使得系统在每一步都无限接近于平衡态。
  • 没有耗散效应 (dissipative effects)，如摩擦 (friction)、粘滞性 (viscosity)、非弹性形变、电流产生的热等。
  • 没有非平衡的热传递，例如跨越有限温度差的热传递。
  • 熵判据 (Entropy Criterion): 一个过程是可逆的，当且仅当系统与环境的总熵变 (total entropy change) 为零：$\mathrm{\Delta }{S}_{tot}=\mathrm{\Delta }{S}_{sys}+\mathrm{\Delta }{S}_{surr}=0$ (Slide 10)。
  • 准静态的绝热过程 ($Q=0$) 是可逆的，因为 $dS=d{Q}_{rev}/T=0$，系统熵不变，环境也无变化，$\mathrm{\Delta }{S}_{tot}=0$ (Slide 12)。
  • 准静态的等温过程 (与温度恒为 $T$ 的热库接触) 是可逆的。如果系统从热库吸收热量 $Q$，则 $\mathrm{\Delta }{S}_{sys}=Q/T$，热库失去热量 $Q$，$\mathrm{\Delta }{S}_{res}=-Q/T$。因此 $\mathrm{\Delta }{S}_{tot}=Q/T-Q/T=0$ (Slide 12)。
  • Slide 3 和 13 中将等容和等压过程标记为不可逆，这通常是指实际操作中，例如将系统突然与一个不同温度的热库接触进行等容加热，或在有摩擦的活塞下进行等压膨胀。这些实际过程涉及有限温差传热或摩擦，导致 $\mathrm{\Delta }{S}_{tot}>0$。然而，理想化的等容和等压过程 可以 作为可逆循环的一部分，只要热量交换是通过一系列无穷小的温差或可逆方式进行的。
• 不可逆过程 (Irreversible Process): 自然界中发生的所有宏观过程都是不可逆的。它们不能自行反向进行。
  • 特征：过程进行速度有限，系统偏离平衡态；存在耗散效应；存在有限温差传热。
  • 总熵总是增加：$\mathrm{\Delta }{S}_{tot}>0$。
  • 例子 (Slide 11, 14, 26):
    • 一个物体由于摩擦而减速停止，其宏观动能转化为内能（热）。反过来，物体的内能自发地转化为宏观动能，让物体重新运动起来，是永远不会发生的 (Slide 11)。
    • 自由膨胀 (Free Expansion): 气体向真空膨胀 (Slide 14)。这是一个快速、非准静态的过程。虽然对于理想气体 $W=0,Q=0,\mathrm{\Delta }U=0$，但过程是高度不可逆的，气体不会自发地收缩回原来的体积。熵是增加的。
    • 跨越有限温差的热传递 (热量从热物体传到冷物体)。
    • 摩擦生热。

热机与效率 (Heat Engines and Efficiency)

(Slide 15, 22)

• 热机 (Heat Engine): 一种将热能转化为有用功的装置。它通常在一个 循环 (cycle) 中工作，意味着工作物质 (working substance, e.g., gas) 经过一系列过程后回到其初始状态 ($\mathrm{\Delta }{U}_{cycle}=0$)。
• 工作原理 (Slide 15):
  1. 从高温热库 ($T_h$) 吸收热量 $Q_h$。
  2. 对外做功 $W_{by}$。
  3. 向低温热库 ($T_c$) 排放废热 $Q_c$。
  4. 循环往复。 注意: 热库是指足够大，以至于吸收或放出热量时其自身温度保持不变的系统。
• 能量守恒 (Energy Conservation): 对于一个完整的循环 $\mathrm{\Delta }{U}_{cycle}=0$，根据热力学第一定律 $Q_{net}=W_{by}$。净吸收的热量 $Q_{net}=Q_h-Q_c$ (我们定义 $Q_h,Q_c,W_{by}$ 均为正值，代表其大小)。所以： $$W_{by}=Q_h-Q_c$$
• 效率 (Efficiency) $ϵ$ (Slide 22): 定义为 “得到的有用功” 与 “付出的代价 (吸收的热量)” 之比。 $$ϵ=\frac{W_{by}}{Q_h}=\frac{Q_h-Q_c}{Q_h}=1-\frac{Q_c}{Q_h}$$ 效率表示有多少从高温热库吸收的热量被转化为了功。因为必须有废热 $Q_c$ 排出 (后面会看到这是第二定律的要求)，所以效率 $ϵ$ 总是小于 1 (或 100%)。

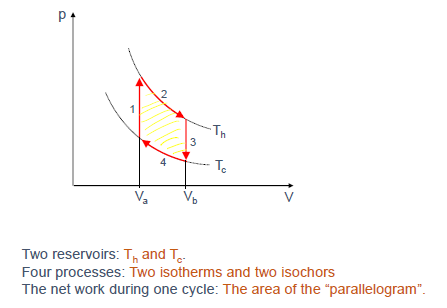
斯特林循环 (Stirling Cycle) - 热机实例

(Slide 16-21)

斯特林循环是一个由两个等温过程和两个等容过程组成的理想循环。

• 过程 1 ($4\to 1$): 等容加热 ($V_a$ 不变, $T$ 从 $T_c$ 升到 $T_h$)。吸收热量 $Q_1=C_V(T_h-T_c)$。
• 过程 2 ($1\to 2$): 等温膨胀 ($T_h$ 不变, $V$ 从 $V_a$ 增到 $V_b$)。吸收热量 $Q_2=W_2=Nk{T}_h\ln (V_b/V_a)$。

• 过程 3 ($2\to 3$): 等容冷却 ($V_b$ 不变, $T$ 从 $T_h$ 降到 $T_c$)。放出热量 $

  Q_3

  = C_V(T_h-T_c)$。

• 过程 4 ($3\to 4$): 等温压缩 ($T_c$ 不变, $V$ 从 $V_b$ 减到 $V_a$)。放出热量 $

  Q_4

  =

  W_4

  = NkT_c \ln(V_b/V_a)$。

• 净功 (Net Work): $W_{by}=W_2+W_4=Nk{T}_h\ln (V_b/V_a)-Nk{T}_c\ln (V_b/V_a)=Nk(T_h-T_c)\ln (V_b/V_a)$ (Slide 19)。这等于 P-V 图上封闭曲线所围的面积。
• 总吸热 $Q_h$: 来自高温过程的热量。在 Slide 20 中定义为 $Q_h=Q_1+Q_2=\alpha Nk(T_h-T_c)+Nk{T}_h\ln (V_b/V_a)$。 (在实际的带回热器 (regenerator) 的斯特林发动机中，$Q_1$ 的热量可以由 $Q_3$ 放出的热量提供，此时 $Q_h$ 仅为 $Q_2$。但按此幻灯片的计算方式，我们用 $Q_1+Q_2$)。
• 效率 (Efficiency): $ϵ=W_{by}/Q_h=\frac{Nk(T_h-T_c)\ln (V_b/V_a)}{\alpha Nk(T_h-T_c)+Nk{T}_h\ln (V_b/V_a)}$。
• 数值算例 (Slide 21): 对于 $V_b=2V_a$, 单原子气体 $\alpha =3/2$, $T_h=373K$, $T_c=273K$，计算得到 $ϵ\approx 16.9\mathrm{\%}$。

热力学第二定律与卡诺效率 (The Second Law and Carnot Efficiency)

(Slide 23-27, 31)

• 热力学第二定律 (The Second Law of Thermodynamics): 有多种等价表述。这里用到的是克劳修斯表述的推论和熵表述：
  • 开尔文-普朗克表述推论: 不可能制造出一种循环工作的热机，只从一个热源吸热，将之完全转化为功，而不在低温热库留下任何其它变化 (即 $Q_c$ 不可能为零)。
  • 熵表述: 在任何涉及孤立系统的过程中，系统的总熵永不减少 ($\mathrm{\Delta }{S}_{tot}\ge 0$)。对于可逆过程 $\mathrm{\Delta }{S}_{tot}=0$，对于不可逆过程 $\mathrm{\Delta }{S}_{tot}>0$。
• 效率上限 (Maximum Efficiency): (Slide 23-24) 考虑任意一个在 $T_h$ 和 $T_c$ 之间工作的热机。在一个循环中，引擎本身熵变 $\mathrm{\Delta }{S}_{engine}=0$。热库的熵变是 $\mathrm{\Delta }{S}_{hot}=-Q_h/T_h$ (失去热量) 和 $\mathrm{\Delta }{S}_{cold}=+Q_c/T_c$ (得到热量)。 根据第二定律，总熵变 $\mathrm{\Delta }{S}_{tot}=\mathrm{\Delta }{S}_{engine}+\mathrm{\Delta }{S}_{hot}+\mathrm{\Delta }{S}_{cold}=0-Q_h/T_h+Q_c/T_c\ge 0$。 整理得到：$\frac{Q_c}{T_c}\ge \frac{Q_h}{T_h}$，即 $\frac{Q_c}{Q_h}\ge \frac{T_c}{T_h}$。 将此代入效率公式 $ϵ=1-Q_c/Q_h$，得到： $$ϵ\le 1-\frac{T_c}{T_h}$$ 这个结果表明，任何在给定温度 $T_h$ 和 $T_c$ 之间工作的热机，其效率不可能超过 $1-T_c/T_h$。这个上限被称为 卡诺效率 (Carnot Efficiency)： $${ϵ}_{Carnot}=1-\frac{T_c}{T_h}$$
  • 这是一个 普适定律 (universal law)，不依赖于工作物质或热机的具体设计。
  • 只有 可逆热机 (reversible engine) 才能达到卡诺效率 (此时 $\mathrm{\Delta }{S}_{tot}=0$，不等号取等号)。
  • 提高效率的方法：提高 $T_h$ 或降低 $T_c$ (Slide 25)。
• 卡诺循环 (Carnot Cycle): (Slide 27) 为了达到卡诺效率，热机必须只由可逆过程组成。卡诺设计了一个理想的可逆循环，由以下四个过程组成：
  1. 等温膨胀 (Isothermal expansion) at $T_h$。
  2. 绝热膨胀 (Adiabatic expansion) (温度从 $T_h$ 降到 $T_c$)。
  3. 等温压缩 (Isothermal compression) at $T_c$。
  4. 绝热压缩 (Adiabatic compression) (温度从 $T_c$ 回到 $T_h$)。 由于所有过程都是可逆的，卡诺循环的效率等于 ${ϵ}_{Carnot}$。
• 效率损失与熵产生 (Efficiency Loss and Entropy Production): (Slide 26, 31) 对于任何不可逆的热机 ($\mathrm{\Delta }{S}_{tot}>0$)，其效率必然低于卡诺效率。效率损失的大小与总熵产生 $\mathrm{\Delta }{S}_{tot}$ 直接相关： $$ϵ={ϵ}_{Carnot}-\frac{T_c\mathrm{\Delta }{S}_{tot}}{Q_h}$$ 要提高效率，就要尽量减少系统中的不可逆性（减少熵产生）。

制冷机与热泵 (Refrigerators and Heat Pumps)

(Slide 28-30)

热机是利用温差做功，反过来，我们可以利用功来传递热量，这就是制冷机和热泵。它们的工作原理本质上是热机循环的逆转。

• 性能系数 (Coefficient of Performance, COP): 用于衡量制冷机和热泵的性能，定义为 “得到的结果” / “付出的代价 (输入的功)”。

• 制冷机 (Refrigerator):
  • 目标：从低温处 ($T_c$) 移走热量 $Q_c$ (使其保持低温)。
  • 代价：需要输入功 $W_{in}$ (注意 $W_{in}$ 在图中标记为 $W_{on}$)。
  • 能量守恒：$Q_h=Q_c+W_{in}$ (向高温环境 $T_h$ 排出总热量 $Q_h$)。
  • 性能系数：$\text{COP}{Ref} = K = \frac{Q_c}{W{in}}$。
  • 卡诺制冷机制冷系数 (上限): $$K_{Carnot}=\frac{T_c}{T_h-T_c}$$
• 热泵 (Heat Pump):
  • 目标：向高温处 ($T_h$) 输送热量 $Q_h$ (例如给房间供暖)。
  • 代价：需要输入功 $W_{in}$。
  • 能量守恒：$Q_h=Q_c+W_{in}$ (从低温环境 $T_c$ 吸收热量 $Q_c$)。
  • 性能系数：$\text{COP}{HP} = K’ = \frac{Q_h}{W{in}}$。
  • 卡诺热泵制热系数 (上限): $$K_{Carnot}^{\prime }=\frac{T_h}{T_h-T_c}$$
  • 关系：$\text{COP}{HP} = \text{COP}{Ref} + 1$。
• 重要特点: 当温差 $T_h-T_c$ 很小时，制冷机和热泵的 COP 可以远大于 1。这意味着它们传递的热量可以远大于驱动它们所需的功。例如，Slide 30 的例子中，只需 8.5W 的功率就能将 70W 的热量从冰箱内部抽出。

Lecture 8: Reversible Processes

热力学基本概念回顾

• 系统 (System) 与环境 (Environment): 在热力学中，我们通常关注一个特定的系统 (例如，气缸中的气体) 以及它周围的环境 (Surroundings)。
• 热机示意图 (Heat Engine Diagram): Slide 2 展示了一个典型的热机模型。
  • 它从高温热源 (Hot Reservoir) $T_H$ 吸收热量 $Q_H$。
  • 一部分能量转化为功 (Work) $W_{out}$ 输出。
  • 剩余的热量 $Q_C$ 排放到低温热源 (Cold Reservoir) $T_C$。
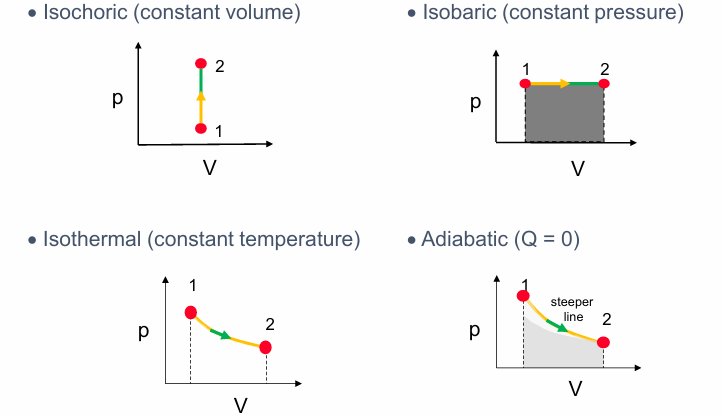
• 四种基本热力学过程 (Four Thermodynamic Processes, Slide 3):
  • 等容过程 (Isochoric Process): 体积 $V$ 保持不变。在 P-V 图上是一条垂直线。
  • 等压过程 (Isobaric Process): 压强 $p$ 保持不变。在 P-V 图上是一条水平线。过程中做的功是 $W=p\mathrm{\Delta }V$，在 P-V 图上是曲线下的面积 (灰色区域)。
  • 等温过程 (Isothermal Process): 温度 $T$ 保持不变。对于理想气体，P-V 图上是一条双曲线 ($p\propto 1/V$)。
  • 绝热过程 (Adiabatic Process): 系统与外界没有热量交换 ($Q=0$)。对于理想气体，P-V 图上也是一条曲线 ($p\propto 1/V^{\gamma }$)，通常比等温线更陡峭 (steeper)。

可逆过程与熵 (Reversible Processes and Entropy)

• 可逆过程的定义: 一个过程是可逆的，意味着系统和环境总能恢复到初始状态，并且在外界不留下任何变化。
• 可逆过程的熵条件 (Entropy Condition for Reversibility): 一个过程是可逆的，其充要条件是系统与环境的总熵变 (Total Entropy Change) 为零。 $$\mathrm{\Delta }{S}_{TOT}=\mathrm{\Delta }{S}_{system}+\mathrm{\Delta }{S}_{environment}=0$$
  • 这意味着在可逆过程中，没有净熵产生 (No net entropy is produced!) (Slide 5)。
• 可逆过程的类型 (Types of Reversible Processes, Slide 5): 在热力学中，只有两种基本类型的过程可以是可逆的：
  1. 准静态绝热过程 (Quasi-static adiabatic processes, $Q=0$)
  2. 准静态等温过程 (Quasi-static isothermal processes, T constant)
     • 准静态 (Quasi-static): 指过程进行得极其缓慢，系统在任何时刻都无限接近于平衡态 (Equilibrium)。这是实现可逆性的必要条件，但不是充分条件 (还需要无摩擦等)。

[!tip] 准静态 vs. 可逆过程 (Quasi-static vs. Reversible Processes)

• 关系:
  • 所有可逆过程都必须是准静态的 (All reversible processes are quasi-static) 。因为如果过程不是缓慢进行的，系统内部就会出现不平衡 (如压强差、温度差)，导致熵产生，从而不可逆。
  • 但并非所有准静态过程都是可逆的 (Not all quasi-static processes are reversible)。例如，一个缓慢进行的有摩擦的过程，虽然是准静态的，但摩擦会产生熵，因此是不可逆的。
  • 技术比喻: 缓慢地 (准静态地) 移动一个物体，如果在有摩擦的表面上移动，能量会因摩擦转化为热量 (熵增加)，这个过程无法完美倒过来让热量变回机械能并将物体推回原处，所以是不可逆的。只有在理想的无摩擦表面上缓慢移动，才可能是可逆的。

非平衡过程 (Non-equilibrium Processes, Slide 6)

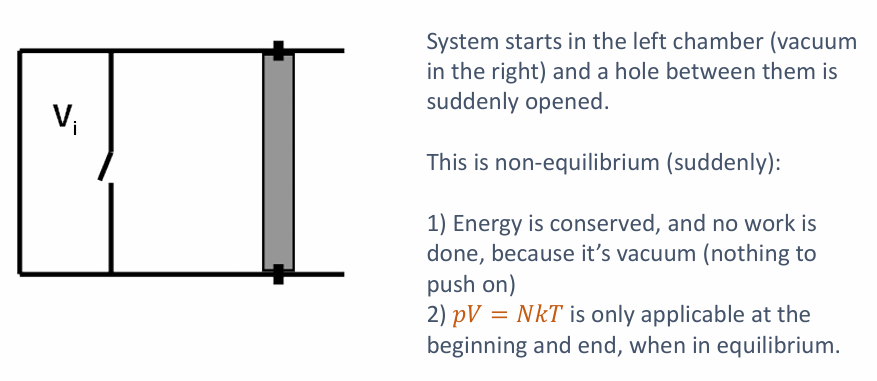
• 自由膨胀 (Free Expansion): Slide 6 的例子是一个典型的非平衡过程。气体突然冲入真空区域。
  • 这是一个快速过程，不是准静态的。
  • 系统在膨胀过程中并不处于平衡态，因此我们不能用 $pV=NkT$ 这样的状态方程来描述中间过程 (只能描述初始和最终的平衡态)。
  • 由于是向真空膨胀，气体不对外做功 ($W=0$)。如果容器绝热 ($Q=0$)，根据热力学第一定律 $\mathrm{\Delta }U=Q-W=0$，理想气体的内能不变，因此温度也不变。
  • 尽管能量守恒且温度可能不变，但这是一个高度不可逆的过程，总熵是显著增加的 ($\mathrm{\Delta }{S}_{TOT}>0$)。

绝热与等温过程详解 (Detailed Look at Adiabatic and Isothermal Processes)

• 绝热过程 (Adiabatic Process):
  • $Q=0$ (系统与外界无热量交换)。
  • 对于可逆 (准静态) 绝热过程，熵变 $\mathrm{\Delta }S=\int dQ/T=0$。系统熵不变。
  • 对于理想气体，该过程遵循 $p{V}^{\gamma }=\text{const}$，其中 $\gamma =C_p/C_v$ 是绝热指数 (adiabatic index)，也等于 $(\alpha +1)/\alpha$，这里 $\alpha =N_{DOF}/2$ (自由度的一半)。
• 等温过程 (Isothermal Process):
  • $T=\text{const}$ (系统与一个恒温热库接触)。
  • 对于可逆 (准静态) 等温过程，系统与热库之间有热量交换 $Q$。
  • 系统熵变 $\mathrm{\Delta }{S}_{sys}=Q/T$
  • 热库 (环境) 熵变 $\mathrm{\Delta }{S}_{res}=-Q/T$ (与系统熵变大小相等，符号相反)。
  • 总熵变 $\mathrm{\Delta }{S}_{tot}=\mathrm{\Delta }{S}_{sys}+\mathrm{\Delta }{S}_{res}=0$。
  • 对于理想气体，该过程遵循 $pV=\text{const}$ (即 $p=\text{const}/V$)。

热机效率与制冷机制冷系数 (Efficiency and COP)

• 通用评价指标 (General Form): 性能 = 你得到的 (What you get) / 你付出的 (What you paid for)。
• 热机效率 (Engine Efficiency, $ϵ$):
  • 得到: 做出的功 $W$。
  • 付出: 从高温热源吸收的热量 $Q_H$ (例如，燃料燃烧产生的热量)。
  • $ϵ=\frac{W}{Q_H}$。根据能量守恒 $W=Q_H-Q_C$，所以 $ϵ=\frac{Q_H-Q_C}{Q_H}=1-\frac{Q_C}{Q_H}$。
• 制冷机性能系数 (Refrigerator COP):
  • 得到: 从低温物体 (冰箱内部) 移走的热量 $Q_C$。
  • 付出: 消耗的功 $W$ (例如，压缩机消耗的电能)。
  • $CO{P}_{ref}=\frac{Q_C}{W}$。
• 热泵性能系数 (Heat Pump COP):
  • 得到: 向高温物体 (室内) 输送的热量 $Q_H$。
  • 付出: 消耗的功 $W$ (例如，电能)。
  • $CO{P}_{HP}=\frac{Q_H}{W}$。
  • 注意 $Q_H=W+Q_C$，所以 $CO{P}_{HP}=\frac{W+Q_C}{W}=1+CO{P}_{ref}$。热泵的 COP 通常大于 1。

卡诺循环与卡诺效率 (Carnot Cycle and Efficiency, Slide 10, 14, 18)

• 卡诺循环 (Carnot Cycle): 由两个可逆等温过程和两个可逆绝热过程组成的理想热力学循环。

• 卡诺定理 (Carnot’s Theorem): 在相同的高温热源 $T_H$ 和低温热源 $T_C$ 之间工作的所有热机中，可逆热机 (如卡诺热机) 的效率最高。所有可逆热机在该条件下效率都相同。

• 卡诺效率 (Carnot Efficiency, ${ϵ}_{Carnot}$): $${ϵ}_{Carnot}=1-\frac{T_C}{T_H}$$
  • 这是理论上的最大效率。注意：温度 $T_H$ 和 $T_C$ 必须使用绝对温标 (开尔文 Kelvin, K)。
  • 对于可逆循环 (卡诺循环)，有 $$\frac{Q_C}{Q_H}=\frac{T_C}{T_H}$$
• 不可逆性对效率的影响 (Inefficiency due to Irreversibility):
  • 对于任何在 $T_H$ 和 $T_C$ 之间工作的热机，总熵变 $\mathrm{\Delta }{S}_{total}=\frac{Q_C}{T_C}-\frac{Q_H}{T_H}\ge 0$ (等号仅对可逆过程成立)。
  • 实际效率 $ϵ$ 与卡诺效率的关系为： $$ϵ=1-\frac{Q_C}{Q_H}=1-\frac{T_C}{T_H}\left(\frac{Q_C/T_C}{Q_H/T_H}\right)$$ 推导: 从 $\mathrm{\Delta }{S}_{total}=\frac{Q_C}{T_C}-\frac{Q_H}{T_H}$ 可得 $\frac{Q_C}{T_C}=\frac{Q_H}{T_H}+\mathrm{\Delta }{S}_{total}$。 所以 $\frac{Q_C}{Q_H}=\frac{T_C}{T_H}+\frac{T_C\mathrm{\Delta }{S}_{total}}{Q_H}$。 代入效率公式 $ϵ=1-\frac{Q_C}{Q_H}$： $$ϵ=1-(\frac{T_C}{T_H}+\frac{T_C\mathrm{\Delta }{S}_{total}}{Q_H})=(1-\frac{T_C}{T_H})-\frac{T_C\mathrm{\Delta }{S}_{total}}{Q_H}$$ 即： $$ϵ={ϵ}_{Carnot}-\frac{T_C\mathrm{\Delta }{S}_{total}}{Q_H}$$
  • 由于 $\mathrm{\Delta }{S}_{total}\ge 0$, $T_C>0$, $Q_H>0$，所以实际效率 $ϵ\le {ϵ}_{Carnot}$。任何不可逆因素 ($\mathrm{\Delta }{S}_{total}>0$) 都会降低热机效率。
  • 卡诺热机是理想化的，现实中无法完全实现，因为它要求过程无限缓慢且没有摩擦等损耗。

可选内容: 理想气体绝热过程公式推导 (Optional: Adiabatic formula)

• Slide 20 提供了一个推导理想气体准静态绝热过程 $P{V}^{\gamma }=\text{const}$ 的过程。
• 它结合了以下三个基本定律：
  1. 理想气体状态方程 (Ideal gas law): $pV=NkT$ 及其微分形式 $pdV+Vdp=NkdT$。
  2. 热力学第一定律 (1st law of Thermo): 对于绝热过程 $dQ=0$，所以 $dU=-pdV$。
  3. 能量均分定理 (Equipartition theorem): 理想气体内能 $U=\frac{N_{DOF}}{2}NkT$，其微分形式 $dU=\frac{N_{DOF}}{2}NkdT$ (其中 $N_{DOF}$ 是每个分子的自由度)。
• 通过联立和积分这些方程，最终可以得到 $P{V}^{\gamma }=\text{const}$，其中 $\gamma =(N_{DOF}/2+1)/(N_{DOF}/2)=C_p/C_v$。

好的同学，我们来一起回顾一下 Lecture 9 关于亥姆霍兹自由能 (Helmholtz Free Energy) 的内容。

这次课我们主要讨论了一个新的热力学势——亥姆霍兹自由能，它是联系宏观热力学和微观统计力学的重要桥梁，并且在描述恒温恒容过程系统所能做的最大功方面非常有用。

我会按照讲义的顺序，结合一些例子和解释，来帮你梳理知识点。

Lecture 9: 亥姆霍兹自由能 (Helmholtz Free Energy)

热力学循环回顾 (Review of Thermodynamic Cycles)

1. 热机 (Heat Engine)

(Slides 3, 4)

• 热机是一种将热能转化为功的装置。它从高温热源 ($T_h$) 吸收热量 $Q_h$，一部分转化为功 $W$，另一部分热量 $Q_c$ 排放到低温热源 ($T_c$)。
• 效率 (Efficiency, $ϵ$): 对所有热机： $$ϵ=\frac{W}{Q_h}=1-\frac{Q_c}{Q_h}$$
• 卡诺循环 (Carnot Cycle):
  • 是一种理想的可逆循环 (Reversible Cycle)，由两个等温过程 (Isothermal Process) 和两个绝热过程 (Adiabatic Process) 组成。
  • 卡诺热机的效率是所有在相同两个热源之间工作的热机中最高的： $${ϵ}_{\text{Carnot}}=1-\frac{T_c}{T_h}$$
  • 对于卡诺循环 (可逆过程): $$\frac{Q_c}{Q_h}=\frac{T_c}{T_h}$$
• 不可逆性与熵 (Irreversibility and Entropy):
  • 实际的热机都是不可逆的 (Irreversible)，这意味着在循环过程中总熵会增加 ($\mathrm{\Delta }{S}_{tot}>0$)。
  • 当存在净的熵增时，热机效率会降低： $$ϵ={ϵ}_{\text{Carnot}}-\frac{T_c\mathrm{\Delta }{S}_{tot}}{Q_H}$$

2. 绝热/等温过程的可逆性 (Adiabatic/Isothermal processes Reversibility)

• 绝热过程 (Adiabatic Process): 系统与外界没有热量交换 ($dQ=0$)。
  • 准静态绝热过程 (Quasi-static adiabatic process) 是可逆的，因为 $\mathrm{\Delta }S=\int \frac{dQ}{T}=0$。
• 等温过程 (Isothermal Process): 系统与恒温热源接触，温度保持不变。
  • 对于准静态等温过程，系统从热源吸收 (或放出) 热量 $dQ$。系统熵变 $\mathrm{\Delta }{S}_{sys}=dQ/T$，热源熵变 $\mathrm{\Delta }{S}_{res}=-dQ/T$。
  • 总熵变 $\mathrm{\Delta }{S}_{tot}=\mathrm{\Delta }{S}_{sys}+\mathrm{\Delta }{S}_{res}=0$。因此，准静态等温过程也是可逆的。

3. 热机的逆行：制冷机与热泵 (Heat Engine in Reverse: Refrigerators and Heat Pumps)

• 如果将卡诺循环反向进行，就得到了制冷机或热泵。它们通过外界做功 $W$，将热量从低温热源 ($T_c$) 转移到高温热源 ($T_h$)。
• 性能系数 (Coefficient of Performance, K) (注意这里不用“效率”):
  • 制冷机 (Refrigerator): 目的是使低温物体保持低温 (我们关心 $Q_c$)。 $$K_{\text{refrigerator}}=\frac{Q_c}{W}=\frac{Q_c}{Q_h-Q_c}=\frac{T_c}{T_h-T_c}(\text{对于理想卡诺制冷机})$$
  • 热泵 (Heat Pump): 目的是使高温物体保持高温 (我们关心 $Q_h$)。 $$K_{\text{heat pump}}=\frac{Q_h}{W}=\frac{Q_h}{Q_h-Q_c}=\frac{T_h}{T_h-T_c}(\text{对于理想卡诺热泵})$$
  • 这里的 $W$ 是我们为制冷机或热泵的运行所付出的代价，比如电费。

4. 制冷的极限 (The Limits of Cooling)

• 从制冷机的性能系数公式 $K_{\text{refrigerator}}=T_c/(T_h-T_c)$ 可以看出，当 $T_c\to 0$ 时，$K\to 0$。
• 这意味着要达到更低的温度，制冷机的性能会急剧下降，需要消耗的功 $W=Q_c/K$ 会急剧增加。
• 结论: 不可能将一个系统冷却到绝对零度 (Absolute Zero)。这是热力学第三定律的一个表述。

可用功与亥姆霍兹自由能 (Available Work and Free Energy)

1. 可用功的推导 (Derivation of Available Work)

• 考虑一个物体 (比如一块砖头，brick) 从初始温度 $T_{brick}$ 冷却到环境温度 $T_{env}$ 。我们想知道一个理想热机能从这个冷却过程中提取多少功 $W_{by}$。
• 根据能量守恒 (热力学第一定律) 和熵的定义 (热力学第二定律，假设卡诺效率)，我们得到： $$W_{by}=-\mathrm{\Delta }{U}_{brick}+T_{env}\mathrm{\Delta }{S}_{brick}$$ 这里：
  • $\mathrm{\Delta }{U}_{brick}$ 是砖头内能 (Internal Energy, $U$) 的变化。砖头降温，$\mathrm{\Delta }{U}_{brick}$ 为负，所以 $-\mathrm{\Delta }{U}_{brick}$ 为正，表示能量被提取出来。
  • $\mathrm{\Delta }{S}_{brick}$ 是砖头熵 (Entropy, $S$) 的变化。砖头降温，熵减少，$\mathrm{\Delta }{S}_{brick}$ 为负。$T_{env}\mathrm{\Delta }{S}_{brick}$ 这一项代表了由于熵变，必须传递给环境的热量的一部分，它减少了可对外做的功。

2. 亥姆霍兹自由能的定义 (Definition of Helmholtz Free Energy)

• 为了方便表示上述可用功，我们定义一个新的态函数，称为亥姆霍兹自由能 (Helmholtz Free Energy, $F$): $$F=U-TS$$ 对于我们讨论的砖块系统，在与温度为 $T_{env}$ 的环境作用时，其自由能可以写为： $$F_{brick}=U_{brick}-T_{env}{S}_{brick}$$
• 那么，当系统经历一个过程，其亥姆霍兹自由能的变化 $\mathrm{\Delta }{F}_{brick}$ (或微小变化 $d{F}_{brick}$) 与最大可提取功 $W_{by}$ (或 $W_{max}$) 的关系是： $$W_{by}=-(U_{brick,final}-U_{brick,initial})+T_{env}(S_{brick,final}-S_{brick,initial})$$ $$W_{by}=-((U_{brick,final}-T_{env}{S}_{brick,final})-(U_{brick,initial}-T_{env}{S}_{brick,initial}))$$ $$W_{by}=-(F_{brick,final}-F_{brick,initial})=-\mathrm{\Delta }{F}_{brick}$$ 或者写成微分形式 (假设卡诺效率)： $$W_{by}=-d{F}_{brick}$$
• 一般情况下，实际做的功会小于这个最大值，即 $W_{by}\le -d{F}_{brick}$。
• $\mathrm{\Delta }F$ 告诉我们系统在等温过程中 (与温度为 $T_{env}$ 的热源接触) 最多可以提取多少功。
• 技术比喻：你可以把亥姆霍兹自由能想象成系统在特定环境温度下“储存”的能够转化为功的“能量潜力”。当系统从一个非平衡态向平衡态转变时，自由能的减少量就等于它能对外做的最大功。就像一个物体在高处拥有重力势能，当它下落到最低点 (平衡态) 时，势能可以转化为其他形式的能量 (功)。亥姆霍兹自由能也类似，系统偏离平衡态时具有较高的自由能，自发趋向平衡态 (自由能最低点) 的过程中，可以对外做功。

3. 自由能与平衡 (Free Energy and Equilibrium)

• 练习 (Exercise, Slides 10, 11):
  • 讲义中计算了一个砖块在 $T_{env}=300\text{K}$ 的环境下，从 $300\text{K}$ 被加热到 $310\text{K}$ ( $\mathrm{\Delta }T=+10\text{K}$ ) 和被冷却到 $290\text{K}$ ( $\mathrm{\Delta }T=-10\text{K}$ ) 时的亥姆霍兹自由能变化 $\mathrm{\Delta }{F}_B$。
  • 使用的公式是： $\mathrm{\Delta }{U}_B=C\mathrm{\Delta }T=C(T_B-300\text{K})$ $\mathrm{\Delta }{S}_B=C\ln (T_B/300\text{K})$ $\mathrm{\Delta }{F}_B=\mathrm{\Delta }{U}_B-(300\text{K})\mathrm{\Delta }{S}_B$
  • 计算结果显示，无论是加热还是冷却，$\mathrm{\Delta }{F}_B$ 都是正的 (加热时 $0.16\text{ kJ}$，冷却时 $0.17\text{ kJ}$)。
  • 这说明当砖块的温度 $T_B$ 等于环境温度 $T_{env}$ ($300\text{K}$) 时，其亥姆霍兹自由能处于最小值。
  • 图像也直观地展示了这一点：$F_B$ 关于 $T_B$ 的曲线在 $T_B=T_{env}=300\text{K}$ 处有极小值。
• 平衡态对应自由能最小 (Equilibrium corresponds to Free Energy Minimum):
  • 我们知道，一个孤立系统达到平衡时，其总熵 $S_{tot}$ 达到最大值。
  • 现在考虑一个系统 (sys) 与一个大的恒温环境 (e, environment or reservoir) 接触，环境温度为 $T_e$。总熵 $S_{tot}=S_{sys}+S_e$。
  • 如果系统从环境中吸收了微小的内能 $dU$ 。那么环境的熵变 $d{S}_e=d{U}_e/T_e=-d{U}_{sys}/T_e$。
  • 总熵的微小变化为： $$d{S}_{tot}=d{S}_{sys}+d{S}_e=d{S}_{sys}-\frac{d{U}_{sys}}{T_e}$$
  • 我们可以整理这个式子： $$d{S}_{tot}=-\frac{(d{U}_{sys}-T_{e}d{S}_{sys})}{T_e}$$
  • 我们定义的亥姆霍兹自由能 $F_{sys}=U_{sys}-T_e{S}_{sys}$ (注意这里的 $T_e$ 是常数，是环境的温度)。其微分形式为 $d{F}_{sys}=d{U}_{sys}-T_{e}d{S}_{sys}-S_{sys}d{T}_e$。如果在恒温条件下 ($d{T}_e=0$)，或者更准确地说，我们定义 $F$ 时用的 $T$ 就是环境温度 $T_e$ (一个常数)，那么对于系统的变化： $$d{F}_{sys}(\text{at constant }{T}_e)=d{U}_{sys}-T_{e}d{S}_{sys}$$
  • 所以： $$d{S}_{tot}=-\frac{d{F}_{sys}}{T_e}$$
  • 这个关系非常重要！它告诉我们：
    • 在一个与恒温热源接触的系统中 (保持恒容)，总熵 $S_{tot}$ 的最大化等价于系统亥姆霍兹自由能 $F_{sys}$ 的最小化。
    • 因为 $T_e$ 是正的，所以 $d{S}_{tot}$ 和 $d{F}_{sys}$ 符号相反。当系统趋于平衡 ($d{S}_{tot}>0$ 或 $d{S}_{tot}=0$ 达到最大值) 时，$d{F}_{sys}<0$ 或 $d{F}_{sys}=0$ (达到最小值)。
  • 因此，在恒温恒容条件下，系统达到平衡态的判据是其亥姆霍兹自由能达到最小值。
  • Slide 12右下角的图示也形象地表明了 $F=U-TS$ 的关系。$F$ 的极小值点对应平衡态。

三、亥姆霍兹自由能的重要性及使用条件

1. 重要性 (Importance)

• 简化平衡判据: 在很多情况下 (特别是恒温恒容)，最大化总熵 $S_{tot}$ (有时计算复杂) 来判断平衡，可以等效地用最小化系统自由能 $F_{sys}$ (通常更容易计算) 来判断。
• 衡量可做功: 当系统偏离平衡态时，其多余的自由能 (excess free energy) $F-F_{equilibrium}$ 表示一个理想热机在该环境下能从系统中提取的最大功。
• 数据可查: 很多材料的自由能数据是可以查表得到的 (例如化学燃料)。
• 后续应用: 亥姆霍兹自由能是后续学习化学势 (Chemical potential)、半导体中载流子浓度、表面吸附、相变等高级内容的基础。

2. 使用亥姆霍兹自由能的条件 (Conditions for using Helmholtz Free Energy)

使用亥姆霍兹自由能作为平衡判据 (即平衡时 $F_{sys}$ 最小) 或计算最大可做功 ($W_{max}=-\mathrm{\Delta }F$) 是有条件的：

1. 系统与大环境接触: 系统与一个大的环境 (热储, thermal reservoir) 相连，环境温度恒为 $T_{env}$。
2. 只有热量交换: 系统与环境之间只有热量可以流动。这意味着系统的体积 (Volume, $V$) 保持不变，粒子数 (Particle number, $N$) 也保持不变。
   • 简而言之，亥姆霍兹自由能适用于恒温 (isothermal)、恒容 (isochoric)、恒定粒子数的过程。

3. 注意事项：与吉布斯自由能的区别 (Caution: Difference from Gibbs Free Energy)

• Maximum $S_{tot}$ Does Not Always Mean Minimum $F_{sys}$ (Helmholtz):
  • 我们在推导 $F_{brick}=U_{brick}-T_{env}{S}_{brick}$ 时，隐含了一个假设，即砖块的体积是恒定的。
  • 如果体积不是恒定的 (例如，系统是一个在恒定大气压下的气体)，那么系统可以通过膨胀或收缩来做功或被做功，这会改变分析。
  • 在更常见的情况下，系统经历的是恒压 (isobaric) 而非恒容过程。这时，我们需要使用另一个自由能，叫做吉布斯自由能 (Gibbs Free Energy, $G$): $$G=U+pV-TS=H-TS$$ 其中 $H=U+pV$ 是焓 (Enthalpy)。$pV$ 这一项考虑了系统在体积变化时所做的功。
  • 亥姆霍兹自由能主要用于恒容过程，而吉布斯自由能用于恒压过程。选择哪种自由能取决于过程的约束条件。

例题

题目：一个热砖块 $T_{brick}=400\text{ K}$，热容 $C=1\text{ J/K}$，与一个 $T_{res}=300\text{ K}$ 的热储接触，通过一个引擎对外做功。问能从砖块中提取的最大功是多少？

这个问题就是计算砖块从 $400\text{ K}$ 冷却到与热储相同的温度 $300\text{ K}$ 过程中，亥姆霍兹自由能的变化的负值。 环境温度 $T_{env}=T_{res}=300\text{ K}$。 初始状态：$T_i=400\text{ K}$ 末状态：$T_f=300\text{ K}$

1. 计算内能变化 $\mathrm{\Delta }{U}_{brick}$: $$\mathrm{\Delta }{U}_{brick}={\int }_{T_i}^{T_f}CdT=C(T_f-T_i)=(1\text{ J/K})(300\text{ K}-400\text{ K})=-100\text{ J}$$
2. 计算熵变 $\mathrm{\Delta }{S}_{brick}$: $$\mathrm{\Delta }{S}_{brick}={\int }_{T_i}^{T_f}\frac{C}{T}dT=C\ln \left(\frac{T_f}{T_i}\right)=(1\text{ J/K})\ln \left(\frac{300}{400}\right)=(1\text{ J/K})\ln (0.75)$$ $\ln (0.75)\approx -0.2877$ $$\mathrm{\Delta }{S}_{brick}\approx -0.2877\text{ J/K}$$
3. 计算最大可提取功 $W_{max}$: $$W_{max}=-\mathrm{\Delta }{F}_{brick}=-(\mathrm{\Delta }{U}_{brick}-T_{env}\mathrm{\Delta }{S}_{brick})=-\mathrm{\Delta }{U}_{brick}+T_{env}\mathrm{\Delta }{S}_{brick}$$ $$W_{max}=-(-100\text{ J})+(300\text{ K})(-0.2877\text{ J/K})$$ $$W_{max}=100\text{ J}-300\times 0.2877\text{ J}=100\text{ J}-86.31\text{ J}=13.69\text{ J}$$ 所以，最大可提取功是 $13.69\text{ J}$。

好的同学，我们继续学习 Lecture 10 的内容，这次课的主题是平衡与化学势 (Equilibrium and Chemical Potential)。这一讲在上一讲亥姆霍兹自由能的基础上，引入了化学势的概念，用来处理有粒子数交换或化学反应的系统平衡问题。

Lecture 10: 平衡与化学势 (Equilibrium and Chemical Potential)

从熵最大化到自由能最小化：引入粒子交换

1. 以往的平衡判据 (Previously…Maximize entropy to find equilibrium)

• 我们之前学习过，对于一个孤立系统，或几个可以相互作用的系统组成的孤立整体，它们达到平衡的条件是总熵最大化 ($d{S}_{tot}=0$)。
• 例如，两个可以交换体积 (Volume) 的系统 (System 1, System 2): 当 $d{S}_{tot}/d{V}_1=0⟹d{S}_1/d{V}_1=d{S}_2/d{V}_2⟹p_1/T_1=p_2/T_2$ (如果同时可以交换能量使得 $T_1=T_2$) $⟹p_1=p_2$。 更准确地，讲义中从 $(\partial S_1/\partial V_1){U_1,N_1} = (\partial S_2/\partial V_2){U_2,N_2}$(\mathrm{假}\mathrm{设}$dV_1 = -dV_2$)，\mathrm{并}\mathrm{利}\mathrm{用}$TdS = dU + pdV \implies (\partial S/\partial V)_{U,N} = p/T$。\mathrm{所}\mathrm{以}\mathrm{平}\mathrm{衡}\mathrm{时}$p_1/T_1 = p_2/T_2$。\mathrm{如}\mathrm{果}\mathrm{它}\mathrm{们}\mathrm{也}\mathrm{处}\mathrm{于}\mathrm{热}\mathrm{平}\mathrm{衡}$T_1=T_2$，\mathrm{则}$p_1=p_2$。\mathrm{讲}\mathrm{义}\mathrm{中}\mathrm{直}\mathrm{接}\mathrm{给}\mathrm{出}\mathrm{了}$(\partial S_1/\partial V_1) = N_1/V_1$\mathrm{和}$(\partial S_2/\partial V_2) = N_2/V_2$(\mathrm{这}\mathrm{实}\mathrm{际}\mathrm{上}\mathrm{是}\mathrm{理}\mathrm{想}\mathrm{气}\mathrm{体}\mathrm{在}\mathrm{特}\mathrm{定}\mathrm{条}\mathrm{件}\mathrm{下}\mathrm{的}\mathrm{简}\mathrm{化}\mathrm{结}\mathrm{果}，\mathrm{更}\mathrm{普}\mathrm{适}\mathrm{的}\mathrm{是}$p/T$)。

• 两个可以交换能量 (Energy) 的系统: 当 $d{S}_{tot}/d{U}_1=0⟹d{S}_1/d{U}_1=d{S}_2/d{U}_2⟹1/T_1=1/T_2⟹T_1=T_2$。 这里 $(\partial S/\partial U{)}_{V,N}=1/T$。

• 现在的新情况: 允许系统间交换粒子数 (Particle numbers)。

2. 自由能、平衡与化学势 (Free Energy, Equilibrium and Chemical Potential)

• 当系统与一个大的恒温热储 (reservoir at temperature $T_{reservoir}$) 接触时，我们已经知道平衡条件是最大化总熵 ($S_{tot}=S_{reservoir}+S_{smal{l}_{s}ystem}$)，这等价于最小化小系统的亥姆霍兹自由能 ($F_{sys}=U_{sys}-T_{reservoir}{S}_{sys}$)。
  • 为什么等价？ 当系统从热储吸收能量 $d{U}_{sys}$ 时，热储能量减少 $d{U}_{reservoir}=-d{U}_{sys}$，热储熵变 $d{S}_{reservoir}=-d{U}_{sys}/T_{reservoir}$。总熵变 $d{S}_{tot}=d{S}_{sys}+d{S}_{reservoir}=d{S}_{sys}-d{U}_{sys}/T_{reservoir}=-(d{U}_{sys}-T_{reservoir}d{S}_{sys})/T_{reservoir}=-d{F}_{sys}/T_{reservoir}$。所以 $S_{tot}$ 最大化对应 $F_{sys}$ 最小化。
  • 使用自由能的好处是，我们只需要关注系统本身的性质和热储的温度，而不需要显式计算热储的熵。
• 考虑两个子系统 (1 和 2) 之间交换粒子:
  • 这两个子系统都与一个共同恒温热储接触，温度为 $T$。
  • 总的自由能 $F_{tot}=F_1+F_2$。
  • 当粒子从系统2转移到系统1时，$d{N}_1>0$ 且 $d{N}_2=-d{N}_1<0$。
  • 在平衡时，总自由能对于粒子数的微小变化应该达到最小值，即 $d{F}_{tot}/d{N}_1=0$。 $$\frac{d{F}_{tot}}{d{N}_1}=\frac{d(F_1+F_2)}{d{N}_1}=\frac{d{F}_1}{d{N}_1}+\frac{d{F}_2}{d{N}_1}$$ 由于 $d{N}_2=-d{N}_1$，所以 $d{F}_2/d{N}_1=(d{F}_2/d{N}_2)(d{N}_2/d{N}_1)=-d{F}_2/d{N}_2$。 因此，平衡条件为： $$\frac{d{F}_1}{d{N}_1}-\frac{d{F}_2}{d{N}_2}=0⟹\frac{d{F}_1}{d{N}_1}=\frac{d{F}_2}{d{N}_2}$$

• 化学势 (Chemical Potential, $\mu$) 的定义: 亥姆霍兹自由能对粒子数的变化率被定义为一个非常重要的量，称为化学势： $${\mu }_i\equiv {\left(\frac{\partial F_i}{\partial N_i}\right)}_{T,V}$$ (下标 $T,V$ 表示在恒温恒容条件下求偏导)。

• 粒子交换的平衡条件: 对于两个交换粒子的子系统，达到平衡时，它们的化学势相等： $${\mu }_1={\mu }_2$$
• 总结一下平衡的演进： 最大化总熵 $\to$ 最小化自由能 (对于与热储接触的系统) $\to$ 化学势相等 (对于可交换粒子的系统)。

化学势的作用

1. 统一平衡条件 (Unifying Equilibrium Conditions)

• 引入化学势使得各种平衡条件在形式上统一起来：
  • 交换体积 (Volume): $(\partial S_1/\partial V_1)=(\partial S_2/\partial V_2)$ (若用熵) $⟹p_1=p_2$ (若$T_1=T_2$)
  • 交换能量 (Energy): $(\partial S_1/\partial U_1)=(\partial S_2/\partial U_2)$ (若用熵) $⟹T_1=T_2$
  • 交换粒子 (Particles): $(\partial F_1/\partial N_1)=(\partial F_2/\partial N_2)$ (若用自由能) $⟹{\mu }_1={\mu }_2$
• 为什么粒子交换用 $dF/dN$ 而不是 $dS/dN$? 当粒子在两个子系统间交换时，如果这两个子系统还与一个共同的外部热储相连，那么粒子移动时可能伴随着能量的吸收或释放，这会影响热储的熵。亥姆霍兹自由能 $F=U-T{S}_{sys}$ (这里的 $T$ 是热储的温度) 已经内含了与热储在恒温下进行热交换的效应。因此，最小化系统的自由能 $F_{sys}$ 是在有热储存在时正确的平衡判据。

2. 粒子流动的方向 (Direction of Particle Flow)

• 当系统未达到平衡时 (例如 ${\mu }_1>{\mu }_2$)：
  • 粒子会自发地从化学势高的地方流向化学势低的地方，以使得总自由能 $F_{tot}$ 最小化。
  • 这与能量从高温流向低温，或物体从高压区移向低压区是类似的。
  • Slide 14 的自由膨胀例子：初始时，左边气体密度高 (化学势高)，右边真空 (化学势低)。移除隔板后，粒子从左向右扩散，直到两边化学势相等 (密度均匀)。

3. 化学势的物理解释 (Physical Interpretation)

(Slide 10)

• 化学势 $\mu$ 可以近似理解为 (在恒温恒容下) 向系统中加入一个粒子所引起的自由能的变化： $$\mu \approx \frac{F(N+1)-F(N)}{1}(\text{at constant }T,V)$$

四、计算化学势 (Computing $\mu$)

1. Example

• 题目：系统在恒定温度 $T$ 和体积 $V$ 下，内能 $U(N)=a{N}^2$，熵 $S(N)=cN$。求化学势 $\mu$。
• 解答：
  1. 首先计算亥姆霍兹自由能 $F(N)=U(N)-TS(N)$: $$F(N)=a{N}^2-T(cN)=a{N}^2-cTN$$
  2. 然后根据定义计算化学势 $\mu =dF/dN$: $$\mu =\frac{dF}{dN}=\frac{d(a{N}^2-cTN)}{dN}=2aN-cT$$
     • 所以正确答案是 (d) $2aN-cT$。

2. 理想气体的化学势 (Chemical Potential for an Ideal Gas)

• 对于理想气体，单位粒子的内能 $u=U/N$ 仅取决于温度 $T$，与 $N$ 无关。很多情况下可以设 $u=0$。
• 熵 $S$ 与 $N$ 的关系： 考虑 $N$ 个粒子分布在 $M$ 个”箱子” (bins) 或量子态中。微观状态数 $\mathrm{\Omega }=M^N/N!$ (假设粒子可分辨且每个箱子可容纳多个粒子，或者粒子不可分辨但大多箱子为空。更准确的玻尔兹曼统计的 Sackur-Tetrode 方程会更复杂，这里是简化模型)。 $$S=k\ln \mathrm{\Omega }=k\ln \left(\frac{M^N}{N!}\right)=k(N\ln M-\ln N!)$$ 其中 $k$ 是玻尔兹曼常数。
• 计算 $(\partial S/\partial N){M,T}$:\mathrm{使}\mathrm{用}\mathrm{斯}\mathrm{特}\mathrm{林}\mathrm{近}\mathrm{似}(Stirlin{g}^{\prime }sApproximation)$\ln N! \approx N \ln N - N$，\mathrm{则}$d(\ln N!)/dN \approx \ln N$。(\mathrm{更}\mathrm{准}\mathrm{确}\mathrm{地}，$(\partial S/\partial N){M,T} = k (\ln M - (\ln N - 1) -1) = k(\ln M - \ln N) = k \ln(M/N)$for$N \gg 1$)\mathrm{讲}\mathrm{义}\mathrm{中}\mathrm{给}\mathrm{出}$(\partial S/\partial N)_M = k \ln(M/N)$(\mathrm{这}\mathrm{里}$M$\mathrm{是}\mathrm{总}\mathrm{的}\mathrm{可}\mathrm{用}\mathrm{状}\mathrm{态}\mathrm{数}，\mathrm{与}\mathrm{体}\mathrm{积}$V$\mathrm{和}\mathrm{温}\mathrm{度}$T$ 有关)。
• 化学势 $\mu$: $$ \mu = \left(\frac{\partial F}{\partial N}\right){T,V} = \left(\frac{\partial (U-TS)}{\partial N}\right){T,V} = u - T\left(\frac{\partial S}{\partial N}\right){T,V} $$ 代入 $(\partial S/\partial N){T,V} = k \ln(M/N)$:$$\mu =u-kT\ln \left(\frac{M}{N}\right)=u+kT\ln \left(\frac{N}{M}\right)$$
• 引入粒子数密度 (particle density) $n=N/V$ 和单位体积量子态数 (number of states per unit volume) $n_Q=M/V$ (也称为量子浓度, quantum concentration，它依赖于温度 $T$ 和粒子质量)。 则 $N/M=(N/V)/(M/V)=n/n_Q$。 所以理想气体的化学势为： $$\mu =u+kT\ln \left(\frac{n}{n_Q}\right)$$
  • 重要结论: 对于理想气体，化学势与粒子数密度的对数成正比。密度越高，化学势越大。
  • 如果将单粒子内能 $u$ 设为能量零点 (例如对于某些问题可以令 $u=0$)，则 $\mu =kT\ln (n/n_Q)$。

五、化学势的应用实例

1. 固溶体中的缺陷 (Solid “Solutions” / Defects in Solids)

• 考虑一个模型：Si 晶体中有 $M$ 个可能的”Si”格点位，其中 $N$ 个位置被”Au”原子占据($N\ll M$)。这可以看作是 Au 在 Si 中的固溶。
• 能量: 每当一个 Au 原子进入 Si 格点时，系统能量增加 $\mathrm{\Delta }$ (相对于 Au 原子在纯 Au 晶体中)。所以总能量 $U(N)=N\mathrm{\Delta }$ (选择纯 Au 的能量为零点)。
• 熵: 熵主要来自 Au 原子在 $M$ 个格点上的排布方式 (构型熵, configurational entropy)，忽略振动等其他贡献。 微观状态数 $\mathrm{\Omega }(N)=(\genfrac{}{}{0ex}{}{M}{N})=\frac{M!}{N!(M-N)!}$。 熵 $S(N)=k\ln \mathrm{\Omega }(N)=k\ln \frac{M!}{N!(M-N)!}$。
• 自由能: $F(N)=U(N)-TS(N)=N\mathrm{\Delta }-kT\ln \frac{M!}{N!(M-N)!}$。
• 平衡条件: 在平衡时，Si 中 Au 的化学势应该等于纯 Au 中 Au 的化学势。如果我们方便地将纯 Au 中 Au 的化学势设为零 (能量零点选择)，那么 Si 中 Au 的化学势在平衡时也应为零。即 $(\partial F/\partial N){T,V} = 0$。$$ \mu = \left(\frac{\partial F}{\partial N}\right){T,V} = \left(\frac{\partial U}{\partial N}\right){T,V} - T\left(\frac{\partial S}{\partial N}\right){T,V} = 0 $$
  • $(\partial U/\partial N{)}_{T,V}=\mathrm{\Delta }$。
  • 使用斯特林近似，对于 $N\ll M$ 的情况： $S(N)\approx k[M\ln M-M-(N\ln N-N)-((M-N)\ln (M-N)-(M-N))]$ $(\partial S/\partial N{)}_{T,V}\approx k[-\ln N+\ln (M-N)]=k\ln \left(\frac{M-N}{N}\right)\approx k\ln \left(\frac{M}{N}\right)$ (因为 $N\ll M$)。 (Slide 18 的推导中用了 $d(\ln X!)/dX\approx \ln X$，这是斯特林近似 $\ln X!\approx X\ln X-X$ 的微分结果。)
  • 所以化学势为： $$\mu =\mathrm{\Delta }-kT\ln \left(\frac{M}{N}\right)$$
• 令 $\mu =0$ 求平衡时的缺陷浓度 $N/M$: $$\mathrm{\Delta }-kT\ln \left(\frac{M}{N}\right)=0⟹kT\ln \left(\frac{M}{N}\right)=\mathrm{\Delta }$$ $$\ln \left(\frac{M}{N}\right)=\frac{\mathrm{\Delta }}{kT}⟹\frac{M}{N}=e^{\mathrm{\Delta }/kT}$$ 所以，平衡时缺陷 (或溶质原子) 的分数浓度为： $$\frac{N}{M}=e^{-\mathrm{\Delta }/kT}$$ 这正是玻尔兹曼因子 (Boltzmann factor) 的形式！这意味着在一定温度下，形成一个能量为 $\mathrm{\Delta }$ 的缺陷的概率与 $e^{-\mathrm{\Delta }/kT}$ 成正比。 也可以表示为缺陷密度 $n=N/V$ 与格点密度 $n_c=M/V$ 的比： $$\frac{n}{n_c}=e^{-\mathrm{\Delta }/kT}$$
• Checkpoint 3 (Sugar in water): 糖在水中的溶解度也遵循类似 $N_{sugar}/N_W\propto e^{-\mathrm{\Delta }/kT}$ 的关系 (这里 $\mathrm{\Delta }$ 是溶解能)。要使溶解的糖最多，即 $N_{sugar}$ 最大，需要最高的温度 $T$。所以选 (c) Near boiling。
• Arrhenius Plot (阿伦尼乌斯图): 如果将 $\ln (\text{concentration})$ 对 $1/T$ 作图，会得到一条直线，其斜率为 $-\mathrm{\Delta }/k$。这种图常用于从实验数据中提取活化能或能量差。图上显示 Cr 的斜率更陡 (负得更多)，说明 Cr 的 $\mathrm{\Delta }/k$ 更大，即 Cr 在硅中的能量成本更高。

2. 本征半导体中的电子和空穴 (Electrons and Holes in Intrinsic Semiconductors)

• 能带结构 (Band Structure): 半导体中电子的能量不是任意的，存在允带和禁带。低能量区为价带 (valence band)，高能量区为导带 (conduction band)，它们之间有一个能量间隔，称为禁带宽度 (energy gap, $\mathrm{\Delta }$ 或 $E_g$)。
• 电子-空穴对 (Electron-hole pairs):
  • 在 $T=0\text{K}$ 时，价带被电子填满，导带为空，没有自由载流子。
  • 当 $T>0\text{K}$ 时，部分电子从价带受热激发到导带，成为自由移动的导电电子 (conduction electrons)。
  • 电子离开价带后，在价带中留下一个空的量子态，称为空穴 (hole)。空穴可以被看作是带正电荷的准粒子，也能自由移动。
  • 在本征半导体 (Intrinsic Semiconductor) 中，电子和空穴是成对产生的，所以电子浓度 $n_e$ 等于空穴浓度 $n_h$。我们称之为本征载流子浓度 $n_i=n_e=n_h$。
• 平衡条件: 导电电子和空穴可以看作是两种理想气体。系统总自由能 $F=F_e+F_h$。当电子-空穴对产生或复合达到平衡时，系统自由能最小。 由于电子和空穴是成对产生的 ($d{N}_e=d{N}_h$)，所以 $dF/d{N}_e=(\partial F_e/\partial N_e)+(\partial F_h/\partial N_h)=0$。 这意味着在平衡时： $${\mu }_e+{\mu }_h=0$$ 其中 ${\mu }_e$ 是导带电子的化学势，${\mu }_h$ 是价带空穴的化学势。
• 计算本征载流子浓度 $n_i$ :
  • 取价带顶的能量为能量零点。则空穴的单粒子内能 $u_h\approx 0$。
  • 导带底的能量为 $\mathrm{\Delta }$。则电子的单粒子内能 $u_e\approx \mathrm{\Delta }$。
  • 根据理想气体化学势公式： ${\mu }_h=kT\ln (n_h/n_{Qh})$ ${\mu }_e=\mathrm{\Delta }+kT\ln (n_e/n_{Qe})$ (其中 $n_{Qe}$ 和 $n_{Qh}$ 分别是电子和空穴的量子浓度)。
  • 代入 ${\mu }_e+{\mu }_h=0$: $$\mathrm{\Delta }+kT\ln \left(\frac{n_e}{n_{Qe}}\right)+kT\ln \left(\frac{n_h}{n_{Qh}}\right)=0$$
  • 由于 $n_e=n_h=n_i$: $$\mathrm{\Delta }+kT\ln \left(\frac{n_i^2}{n_{Qe}{n}_{Qh}}\right)=0$$ $$\ln \left(\frac{n_i^2}{n_{Qe}{n}_{Qh}}\right)=-\frac{\mathrm{\Delta }}{kT}$$ $$n_i^2=n_{Qe}{n}_{Qh}{e}^{-\mathrm{\Delta }/kT}$$
  • 所以本征载流子浓度为： $$n_i=\sqrt{n_{Qe}{n}_{Qh}}{e}^{-\mathrm{\Delta }/(2kT)}$$ 如果定义一个等效的量子浓度 $n_Q=\sqrt{n_{Qe}{n}_{Qh}}$ (有时也写作 $N_C{N}_V$ 的形式，其中 $N_C,N_V$ 是导带和价带的有效状态密度)，则： $$n_i=n_Q{e}^{-\mathrm{\Delta }/(2kT)}$$
  • 这个结果表明，本征载流子浓度随温度指数增长，且强烈依赖于禁带宽度 $\mathrm{\Delta }$。$\mathrm{\Delta }$ 越大，$n_i$ 越小。
• Slide 28 的问题: $n_Q$ 的值对于不同材料不同，且不简单等于用电子质量 $m_e$ 计算的值，是因为电子和空穴在晶格中运动时，受到晶格势场的作用，表现出有效质量 (effective mass) $m_{e,effective}$ 和 $m_{h,effective}$，它们通常不等于自由电子质量，且彼此也不同。因此 $n_Q$ 通常作为经验参数处理。
• Slide 30 的 Checkpoint: 要使导电电子数与总电子数的比例 $N_c/N$ (近似于 $n_i/N_{tota{l}_{v}alenc{e}_{e}lectrons}$) 最大，需要 $n_i$ 最大。根据 $n_i\propto e^{-\mathrm{\Delta }/(2kT)}$，在相同温度 $T$ 下，$n_i$ 最大对应于禁带宽度 $\mathrm{\Delta }$ 最小的材料。表格中 PbS 的 $\mathrm{\Delta }=0.37\text{ eV}$ 最小。所以选 (e) PbS。

3. 数字温度计 (Digital Thermometers)

• 半导体材料 (如热敏电阻, thermistor) 的电阻率强烈依赖于温度 (因为载流子浓度 $n_i$ 随温度指数变化)。这种电阻随温度的快速 (指数级) 变化特性被用于制造数字温度计。

由非平衡化学势做功 (Work from Free Energy Due to Non-equilibrium $\mu$)

• 考虑 $N$ 个粒子在温度 $T$ 下的等温膨胀。我们知道系统做的功 $W_{by}=NkT\ln (V_f/V_i)$。
• 这也可以从自由能变化的角度来看：$W_{by}=-\mathrm{\Delta }F=-(\mathrm{\Delta }U-T\mathrm{\Delta }S)$。
• 对于理想气体的等温膨胀，$\mathrm{\Delta }U=0$ (内能只与温度有关)。所以 $W_{by}=T\mathrm{\Delta }S$。
• 这表明，即使是旧的物理过程 (如理想气体等温膨胀)，也可以用新的语言 (自由能、化学势) 来描述。初始时，如果气体被限制在 $V_i$，然后膨胀到 $V_f$，可以看作是由于初始（如果想象有隔板）和最终状态之间存在化学势（或压强，与化学势相关）的非平衡，系统对外做功。

Lecture 11: Gibs Free Energy

核心概念梳理

1. 数学准备：微分 (Differentials)

• 应用到热力学函数: 比如亥姆霍兹自由能 (Helmholtz Free Energy) $F=U-TS$ (Slide 5)。它的微分是： $$dF=dU-d(TS)$$ 应用乘法法则于 $d(TS)$: $$d(TS)=TdS+SdT$$ 所以： $$dF=dU-TdS-SdT$$
• 计算有限变化: 从初始状态 $i$ 到最终状态 $e$ 的有限变化 $\mathrm{\Delta }g$ 可以通过对微分 $dg$ 积分得到 (Slide 6)。如果 $f=\frac{dg}{dh}$，那么 $dg=fdh$。要计算 $\mathrm{\Delta }g$，我们需要对 $fdh$ 进行积分： $$\mathrm{\Delta }g={\int }_{h(f_i)}^{h(f_e)}fdh$$ 注意积分上下限是对应于 $f_i$ 和 $f_e$ 的 $h$ 的值。

2. 热力学基本关系 (Fundamental Relation of Thermodynamics)

(Slides 2, 15, 18, 28)

这是热力学中一个非常核心的方程，它联系了内能 (Internal Energy) $U$、熵 (Entropy) $S$、体积 (Volume) $V$ 和粒子数 (Particle Number) $N$ 的变化。

• 熵的微分形式 (Slide 15): $$ dS = \left(\frac{\partial S}{\partial U}\right){V,N} dU + \left(\frac{\partial S}{\partial V}\right){U,N} dV + \left(\frac{\partial S}{\partial N}\right){U,V} dN $$ 利用热力学关系 $1/T = (\partial S/\partial U){V,N}$,$p/T = (\partial S/\partial V){U,N}$,\mathrm{和}$-\mu/T = (\partial S/\partial N){U,V}$(\mathrm{其}\mathrm{中}$\mu$\mathrm{是}\mathrm{化}\mathrm{学}\mathrm{势}ChemicalPotential)，\mathrm{我}\mathrm{们}\mathrm{可}\mathrm{以}\mathrm{得}\mathrm{到}：$$dS=\frac{1}{T}dU+\frac{p}{T}dV-\frac{\mu }{T}dN$$
• 内能的微分形式 (Slide 18, 20, 28): 更常见的形式是表示 $dU$: $$dU=TdS-pdV+\mu dN$$ 这个方程适用于任何准静态过程 (quasi-static process) 的简单系统。
  • 把这个方程想象成描述一个系统能量“预算”的公式。当系统的熵、体积或粒子数发生微小变化时，其内能会如何相应地改变。$TdS$ 是热量交换项，$-pdV$ 是体积功项，$\mu dN$ 是与粒子数变化相关的化学功。

3. 亥姆霍兹自由能 (Helmholtz Free Energy, F)

(Slides 5, 12, 20, 21, 28)

• 定义 (Slide 12, 20): $$F=U-TS$$
• 微分形式 (Slide 20): 从 $dF=dU-TdS-SdT$，代入 $dU=TdS-pdV+\mu dN$: $$dF=(TdS-pdV+\mu dN)-TdS-SdT$$ $$dF=-SdT-pdV+\mu dN$$
• 适用条件与意义:
  • 当系统与恒温热源接触，且体积保持不变时 (即 $T$ 和 $V$ 恒定)，亥姆霍兹自由能的变化 $\mathrm{\Delta }F$ 可以判断过程的自发性。
  • 在恒温恒容 ($dT=0,dV=0$) 条件下，一个自发过程会使得系统的亥姆霍兹自由能减小 ($\mathrm{\Delta }F\le 0$)。
  • 平衡态时，$F$ 达到最小值 ($dF=0$) (Slide 21)。
  • $W_{max}=-\mathrm{\Delta }F$ 代表恒温可逆过程中系统对外做的最大功。

4. 吉布斯自由能 (Gibbs Free Energy, G)

(Slides 2, 11, 12, 13, 18, 20, 22, 23, 25, 28)

• 引入原因 (Slide 11): 在很多实际情况下，尤其是化学反应，系统通常与恒温恒压的环境接触 (例如，在敞口烧杯中进行的反应，压力为大气压，温度为室温)。亥姆霍兹自由能适用于恒容过程，而对于恒压过程，我们需要一个新的热力学势——吉布斯自由能。 $pV$ 项考虑了在体积变化过程中系统对环境做的功。

• 定义 (Slide 11, 12, 20): $$G=U+pV-TS$$ 也可以写成 $G=H-TS$ (其中 $H=U+pV$ 是焓 Enthalpy)，或者 $G=F+pV$。

• 微分形式 (Slide 18, 20): 从 $G=F+pV$ 出发，$dG=dF+d(pV)=dF+pdV+Vdp$。 代入 $dF=-SdT-pdV+\mu dN$: $$dG=(-SdT-pdV+\mu dN)+pdV+Vdp$$ $$dG=-SdT+Vdp+\mu dN$$
• 适用条件与意义 (Slide 2, 13, 22, 23):
  • 当系统与恒温恒压环境接触时 (即 $T$ 和 $P$ 恒定)，吉布斯自由能的变化 $\mathrm{\Delta }G$ 可以判断过程的自发性。
  • 在恒温恒压 ($dT=0,dp=0$) 条件下：
    • $\mathrm{\Delta }G<0$: 过程自发进行 (spontaneous)。
    • $\mathrm{\Delta }G>0$: 过程非自发 (non-spontaneous)，需要外界做功才能发生。
    • $\mathrm{\Delta }G=0$: 系统处于平衡态 (equilibrium)。
  • 平衡态时，$G$ 达到最小值 ($dG=0$)。
  • $W_{useful,max}=-\mathrm{\Delta }G$ 代表恒温恒压可逆过程中系统对外做的最大非体积功 (例如电功)。

5. 化学势 (Chemical Potential, μ)

(Slides 7, 8, 10, 17, 18, 19, 24, 25, 28)

• 定义 (Slide 20, 28): 化学势是当其他条件 (如 $S,V$ 或 $T,V$ 或 $T,P$) 不变时，向系统中加入一个粒子所引起的能量 (如 $U,F,G$) 的变化。 $$ \mu = \left(\frac{\partial U}{\partial N}\right){S,V} = \left(\frac{\partial F}{\partial N}\right){T,V} = \left(\frac{\partial G}{\partial N}\right)_{T,P} $$
• 物理意义:
  • 衡量粒子“逃逸”或“进入”系统的趋势。如果一个区域的化学势高，粒子倾向于离开该区域。
  • 在多相或多组分系统中，当达到平衡时，各相或各组分之间可自由交换的粒子的化学势相等。
  • 技术比喻: 化学势类似于物质的“浓度压力”或“化学压力”。物质会自发地从化学势高的地方流向化学势低的地方，直到各处化学势相等，达到平衡。就像温度决定热量流动方向，压力决定气体流动方向一样。
• $G=\mu N$ (Slides 19, 25, 28):
  • 对于恒定 $T,P$ 下的单组分系统，吉布斯自由能可以简单表示为 $G=\mu N$。这是因为 $G$ 是广延量 (extensive property)，$\mu$ 是强度量 (intensive property)。
  • Slide 19 通过理想气体的例子说明，在恒温恒压下，两个相连的容器，尽管粒子数 $N_A,N_B$ 可以不同，但平衡时密度相同，化学势 ${\mu }_A={\mu }_B$，且这个化学势不依赖于容器中有多少粒子。
  • Slide 25 指出，当有多种相态 (气、液、固) 共存时，为了使总的 $G={\mu }_{gas}{N}_{gas}+{\mu }_{liquid}{N}_{liquid}+{\mu }_{solid}{N}_{solid}$ 最小化，粒子会倾向于聚集在化学势最低的那个相态中。
  • 在给定压强与温度下，物质的固态、液态以及气态的密度是固定的。添加更多的固体、液体或者气体只会改变该物质的体积，不会改变密度与化学势。化学势与粒子数无关

    应用与实例

1. 化学平衡 (Chemical Equilibrium)

(Slide 7) 对于一个化学反应 $aA+bB\leftrightarrow cC$:

• 在平衡时，总的自由能 ($F$ 或 $G$，取决于条件) 达到最小值，因此 $dF=0$ 或 $dG=0$。
• 对于恒温恒容条件 (使用 $F$) 或恒温恒压条件 (使用 $G$)，可以导出平衡条件： $$a{\mu }_A+b{\mu }_B=c{\mu }_C$$ 其中 ${\mu }_A,{\mu }_B,{\mu }_C$ 分别是组分 A, B, C 的化学势。

2. 大气定律 (The Law of Atmospheres)

(Slide 8)

• 考虑不同高度的两部分气体，它们可以交换粒子，整个大气是热源。
• 平衡时，两部分气体的化学势相等: ${\mu }_1={\mu }_2$。
• 对于理想气体，化学势表达式为 $\mu =kT\ln (n/n_Q)+U_{ext}$，其中 $U_{ext}$ 是外部势能。这里 $U_{ext,1}=0$, $U_{ext,2}=mgh$。
• ${\mu }_1=kT\ln (n_1/n_Q)$
• ${\mu }_2=kT\ln (n_2/n_Q)+mgh$
• 令 ${\mu }_1={\mu }_2$，可以解出粒子数密度 $n_2/n_1=e^{-mgh/kT}$。
• 结合理想气体状态方程 $p=nkT$ (温度 $T_1=T_2$ 处于平衡)，得到 $p_2/p_1=e^{-mgh/kT}$。

3. 固-气平衡：蒸汽压 (Solid-gas equilibrium: vapor pressure)

(Slide 10)

• 考虑固相和气相在恒定体积和温度下达到平衡 (例如，密闭容器中的干冰 $C{O}_2$)。
• 此时应使用亥姆霍兹自由能 $F$。但通常化学势的讨论更直接。
• 平衡条件是固相的化学势等于气相的化学势: ${\mu }_s={\mu }_g$。
• 对于固体，如果忽略其熵，${\mu }_s\approx -\mathrm{\Delta }$ (其中 $\mathrm{\Delta }$ 是将一个原子从固体中移到真空中所需的能量，即结合能)。
• 对于理想气体，${\mu }_g=kT\ln (n/n_Q)=kT\ln (p/p_Q)$ (其中 $n_Q$ 是量子浓度， $p_Q=n_{Q}kT$)。
• 令 ${\mu }_s={\mu }_g$: $$kT\ln (p/p_Q)=-\mathrm{\Delta }$$ $$p=p_Q{e}^{-\mathrm{\Delta }/kT}$$ 这个 $p$ 就是该温度下的饱和蒸汽压 (vapor pressure) $p_{vapor}$。
• 如果实际气体压强 $p<p_{vapor}$，固体会升华 (sublimation) 或液体会蒸发 (evaporation)，直到气压达到 $p_{vapor}$。

4. 水的结冰自发性 (Spontaneity of Water Freezing)

(Slide 14)

• 这是一个判断过程自发性的例子，通常在恒压下发生 (大气压)，所以使用吉布斯自由能。
• 给定 $\mathrm{\Delta }H$ (焓变) 和 $\mathrm{\Delta }S$ (熵变) 以及温度 $T$。
• 计算 $\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S$。
  • 如果 $\mathrm{\Delta }G<0$，在给定温度下结冰是自发的。
  • 如果 $\mathrm{\Delta }G>0$，结冰非自发 (冰会融化)。
  • 如果 $\mathrm{\Delta }G=0$，冰水共存，处于平衡态 (此时 $T$ 为熔点)。 例如，在 $-{10}^{\circ }C(263K)$ 时，$\mathrm{\Delta }H=-6.01\text{ kJ/mol}$，$\mathrm{\Delta }S=-22\text{ J/mol K}=-0.022\text{ kJ/mol K}$。 $$\mathrm{\Delta }G=-6.01\text{ kJ/mol}-(263\text{ K})(-0.022\text{ kJ/mol K})$$ $$\mathrm{\Delta }G=-6.01+5.786=-0.224\text{ kJ/mol}$$ 因为 $\mathrm{\Delta }G<0$，所以在 $-{10}^{\circ }C$ 时水结冰是自发过程。

5. 描述过程：等温膨胀 (Describing a process)

(Slide 18)

• 考虑单原子理想气体在恒温 $T$、恒定粒子数 $N$ 条件下从 $p_i$ 膨胀到 $p_f$。计算吉布斯自由能的变化 $\mathrm{\Delta }G$。
• 我们有 $dG=Vdp-SdT+\mu dN$。
• 由于 $T$ 和 $N$ 恒定，所以 $dT=0,dN=0$。 $$dG=Vdp$$
• 积分得到 $\mathrm{\Delta }G$: $$\mathrm{\Delta }G={\int }_{p_i}^{p_f}Vdp$$
• 对于理想气体，$pV=NkT\Rightarrow V=NkT/p$。 $$\mathrm{\Delta }G={\int }_{p_i}^{p_f}\frac{NkT}{p}dp=NkT{\int }_{p_i}^{p_f}\frac{1}{p}dp$$ $$\mathrm{\Delta }G=NkT\ln \left(\frac{p_f}{p_i}\right)$$

平衡条件的策略 (Strategy for equilibrium conditions)

系统总是趋向于使其总熵 (系统+环境) 最大化的状态。自由能 $F$ 和 $G$ 是在特定约束条件下，仅用系统本身的性质来判断平衡和自发性的工具。

1. 孤立系统 (Closed system) (恒定 $U,V,N$):
   • 最大化总熵 $S_{tot}$ (Slide 23)。
   • 这通常意味着系统内部达到均匀。
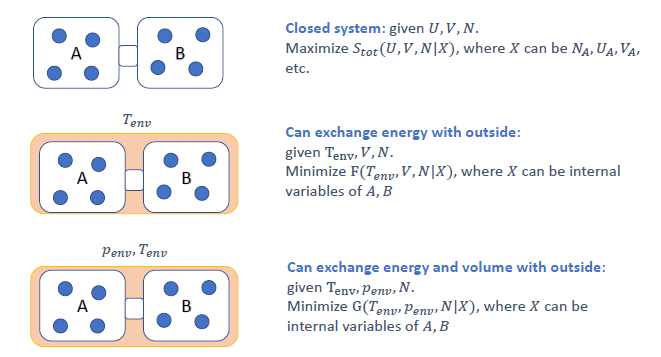
2. 恒温恒容系统 (Constant T, V, N) (可以与外界交换能量):

   • 最小化亥姆霍兹自由能 $F(T, V, N

     X)$，\mathrm{其}\mathrm{中}$X$\mathrm{是}\mathrm{内}\mathrm{部}\mathrm{变}\mathrm{量}(\mathrm{例}\mathrm{如}，\mathrm{两}\mathrm{相}\mathrm{中}\mathrm{的}\mathrm{粒}\mathrm{子}\mathrm{数}\mathrm{分}\mathrm{配}$N_{gas}, N_{solid}$，如 Slide 21)。

   • 策略 (Slide 21):
     1. 使用 $F=U-TS$。
     2. 找到可以变化的内部变量 $x$ (例如 $N_{gas}$，而 $N_{solid}=N_{total}-N_{gas}$)。
     3. 设置 $\frac{dF}{dx}=0$，解出平衡条件。
3. 恒温恒压系统 (Constant T, P, N) (可以与外界交换能量和体积):

   • 最小化吉布斯自由能 $G(T, P, N

     X)$ (Slide 23)。

   • 策略 (Slide 22):
     1. 使用 $G=U+pV-TS$。
     2. 找到可以变化的内部变量 $x$。
     3. 设置 $\frac{dG}{dx}=0$，解出平衡条件。

总结各种热力学势 (Slide 20, 28)

量 (Quantity)	定义 (Definition)	微分 (Differential)	控制变量 (Control variables)
熵 (Entropy, S)	$S=k\ln \mathrm{\Omega }$	$dS=\frac{1}{T}dU+\frac{p}{T}dV-\frac{\mu }{T}dN$	$U,V,N$
亥姆霍兹自由能 (F)	$F=U-TS$	$dF=-SdT-pdV+\mu dN$	$T,V,N$
吉布斯自由能 (G)	$G=U-TS+pV$	$dG=-SdT+Vdp+\mu dN$	$T,p,N$

以及最根本的内能微分形式： $$dU=TdS-pdV+\mu dN$$

Lecture 12: Phases

核心概念：相、相图与化学势

1. 相与相图 (Phases and Phase Diagrams)

(Slides 2, 3, 10, 20, 21, 22)

• 什么是相 (Phase)? (Slide 3)
  • 物质在其物理性质 (如密度、晶体结构) 在宏观上均匀一致的状态。常见的三相是固相 (Solid)、液相 (Liquid) 和气相 (Gas)。
  • 微观差异:
    • 固相: 原子/分子有固定的相对位置，排列有序。熵 (Entropy) $S$ 较低。
    • 液相: 原子/分子间关系较松散，仍有一定关联，但可以流动。熵比固相高。
    • 气相: 原子/分子间几乎没有关联，运动自由。熵通常远大于液相和固相。
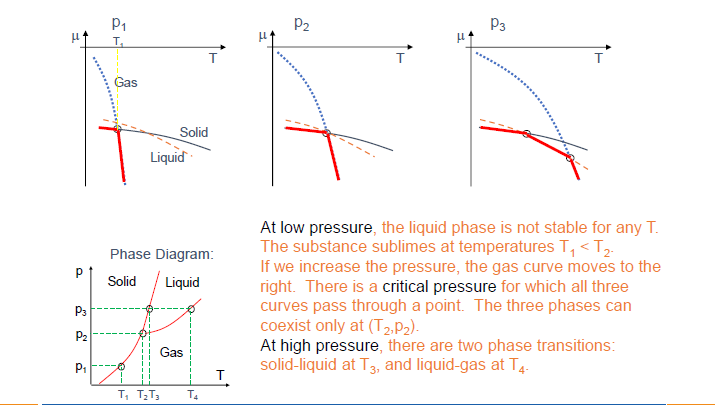
• 相图 (Phase Diagram) (Slides 2, 9, 10, 20, 21, 22)
  • 通常是压力-温度 ($p-T$) 图，显示在不同 $p,T$ 条件下物质的稳定相态。
  • 相界线 (Phase boundaries): 图中的线表示两种相可以共存 (处于平衡) 的 $p,T$ 条件。例如，液-气界线是沸点随压力的变化曲线。
  • 三相点 (Triple point): 三条相界线交汇于一点，表示固、液、气三相可以同时平衡共存的唯一 $p,T$ 条件。 (Slide 9, 10, 22)
  • 临界点 (Critical point): 液-气相界线的终点。超过此点，液相和气相无法区分，物质处于超临界流体 (Supercritical fluid) 状态。(Slide 22 for CO2)
  • 普遍规律: 在 $p-T$ 平面的大部分区域，只有一种相是稳定的 (Slide 10)。

2. 相平衡的热力学判据：吉布斯自由能与化学势

(Slides 4, 5, 6, 7, 8, 9)

• 恒温恒压下的平衡 (Slide 4):
  • 在恒定的温度 $T$ 和压力 $p$ 条件下，系统达到平衡时，其吉布斯自由能 (Gibbs Free Energy) $G$ 最小。
  • 对于一个可以存在于多个相态 (如气相、液相、固相) 的纯物质，其总吉布斯自由能为： $$G={\mu }_{gas}{N}_{gas}+{\mu }_{liquid}{N}_{liquid}+{\mu }_{solid}{N}_{solid}$$ 其中 ${\mu }_i$ 是第 $i$ 相的化学势 (Chemical Potential)，$N_i$ 是第 $i$ 相的粒子数。
  • 核心判据: 为了使 $G$ 最小，粒子会自发地从化学势高的相转移到化学势低的相。因此，在平衡时，所有共存相的化学势必须相等。如果只有一个相稳定，那么该相的化学势是所有可能相中最低的。
• 化学势 $\mu$ 对 $T$ 和 $p$ 的依赖关系 (Slide 6):
  • 我们知道对于单组分系统，$G=N\mu$。其微分形式为 $dG=Vdp-SdT$ (当 $N$ 固定时)。
  • 因此，$Nd\mu =Vdp-SdT$ (这里假设 $N$ 固定，我们考察的是单位粒子或单位摩尔量的化学势如何随 $T,P$ 变化)。
  • 所以，化学势的微分形式为： $$d\mu =\left(\frac{V}{N}\right)dp-\left(\frac{S}{N}\right)dT=vdp-sdT$$ 其中 $v=V/N$ 是单位粒子体积 (或摩尔体积)，$s=S/N$ 是单位粒子熵 (或摩尔熵)。
  • 这意味着：
    • ${\left(\frac{\partial \mu }{\partial p}\right)}_T=v$: 在恒温下，化学势随压力的变化率等于单位粒子体积。因为 $v>0$，所以 $\mu$ 随 $p$ 的增加而增加。
    • ${\left(\frac{\partial \mu }{\partial T}\right)}_p=-s$: 在恒压下，化学势随温度的变化率等于负的单位粒子熵。因为 $s>0$，所以 $\mu$ 随 $T$ 的增加而减小。
• 理解相界线 (Slides 7, 8, 9):
  • $\mu$ vs. $p$ 曲线 (恒T) (Slide 7):
    • 曲线的斜率是 $v$。密度更高的相 ($v$ 更小) 的 $\mu -p$ 曲线斜率更小。
    • 当两条 $\mu -p$ 曲线相交时，意味着两相在该压力下化学势相等，可以共存。
  • $\mu$ vs. $T$ 曲线 (恒P) (Slide 8):
    • 曲线的斜率是 $-s$。熵越大的相，其 $\mu -T$ 曲线的斜率越负 (即下降得越陡峭)。
    • 通常 $s_{gas}>s_{liquid}>s_{solid}$，所以气相的 $\mu -T$ 曲线最陡峭，固相最平缓。
    • Slide 8 的问题：哪个曲线可以代表一个普适物理系统？所有曲线的斜率都应该是负的。且因为 $s$ 随 $T$ 增加 (因为 $c_p>0$, $(\partial s/\partial T{)}_p=c_p/T$)，所以 $-s$ 应该变得更负，即曲线是向下凹的 (concave down)。图中的曲线 (a), (b), (c) 都满足向下凹且斜率为负。因此 (d) All of the above 可能是预期的答案，因为它们都可能代表某一相在一定温度范围内的行为。
  • 从 $\mu -T$ 曲线构建 $p-T$ 相图 (Slide 9):
    • 对于固定的压力 $p_1,p_2,p_3$，画出各相的 $\mu -T$ 曲线。
    • 在任一温度 $T$，化学势最低的相是稳定相。
    • 曲线的交点对应相变温度。例如，在 $p_1$ 下，$T_1$ 是升华点 (固-气转变)。
    • 改变压力会移动这些 $\mu -T$ 曲线 (尤其是气相的，因为它对压力敏感)。例如，增加压力会显著增加 ${\mu }_{gas}$ (理想气体 ${\mu }_{gas}=kT\ln (p/p_Q)$)，使其曲线向上移动。这会导致相变温度的变化。
    • 三条曲线在一点相交的 $(T,p)$ 组合即为三相点 (例如图中的 $T_2,p_2$)。

• 理想气体的化学势回顾 (Slide 5): $${\mu }_g=kT\ln \left(\frac{n}{n_Q}\right)=kT\ln \left(\frac{p}{p_Q}\right)$$ 其中量子浓度 $n_Q\propto T^{3/2}$，所以量子压力 $p_Q=n_{Q}kT\propto T^{5/2}$。
  • 通常情况下 ($n\ll n_Q$ 或 $p\ll p_Q$)，${\mu }_g$ 是负的。
  • ${\mu }_g$ 随压力 $p$ 对数增加，随温度 $T$ 近似线性增加 (实际上由于 $p_Q$ 对 $T$ 的依赖，关系更复杂，导致 $\mu -T$ 曲线向下弯曲，如图中所示，恒压时 $\mu$ 随 $T$ 增加而减少)。
  • Slide 5 的图示：恒压下，温度升高，$\mu$ 减小。恒温下，压力升高，$\mu$ 增大。

相变潜热 (Latent Heat) 与焓 (Enthalpy)

• 潜热 (Latent Heat, $Q_L$ 或 $L$) :
  • 在相变过程中，物质在温度不变的情况下吸收或放出的热量。
  • 例如，在恒压下加热液体，当达到沸点时，继续加热，温度保持不变，直到所有液体都变成气体。这期间吸收的热量就是汽化潜热。
  • 从热力学第一定律 $Q=\mathrm{\Delta }U+p\mathrm{\Delta }V$ (恒压过程)。这部分能量用于增加内能 (克服分子间作用力) 和对外做膨胀功。
• 焓 (Enthalpy, $H$) :
  • 定义: $H=U+pV$。
  • 在恒压过程中，系统吸收的热量等于其焓变: $Q_p=\mathrm{\Delta }H$。（热力学第一定律）
  • 因此，相变潜热等于相变过程中的焓变： $$Q_L=\mathrm{\Delta }{H}_{transition}$$ 例如，汽化热 $\mathrm{\Delta }{H}_{lg}=H_{gas}-H_{liquid}$。
  • 相变过程也是熵变过程，在可逆相变 (温度恒定) 时： $$\mathrm{\Delta }S=\frac{Q_L}{T}=\frac{\mathrm{\Delta }H}{T}$$
• 熵变的计算示例 (Slide 13): 水在 1 atm 结冰时的摩尔熵变。
  • $Q_L$ (熔化热，从冰到水) $=333\text{ J/g}$。结冰时是放出热量，所以 $\mathrm{\Delta }{H}_{freezing}=-333\text{ J/g}$。
  • $T=0^{\circ }C=273\text{ K}$。
  • 摩尔质量 $M=18\text{ g/mol}$。
  • $\mathrm{\Delta }{S}_{freezing,molar}=\frac{-333\text{ J/g}\times 18\text{ g/mol}}{273\text{ K}}\approx -22.0\text{ J/(mol K)}$。
  • 负号表示熵减少，符合从无序度较高的液相到有序度较高的固相的转变。
  • 每个水分子的玻尔兹曼熵 $\sigma =S/N_A{k}_B$ 变化约为 $-2.73$。这意味着液态时每个分子对应的微观状态数大约是固态时的 $e^{2.73}\approx 15$ 倍。

相变过程中相关量变化

Lecture12 Homework2 平衡温度、恒压状态下

• $\mathrm{\Delta }H=\mathrm{\Delta }Q$
• $\mathrm{\Delta }S=\frac{\mathrm{\Delta }H}{T}$
• $\mathrm{\Delta }G=0$ (相变点两种相处于平衡状态)
• 体积变化 $\mathrm{\Delta }V=\frac{\mathrm{\Delta }NkT}{p}$

• 内能变化 $\mathrm{\Delta }U=\mathrm{\Delta }H-p\mathrm{\Delta }V$

• Lecture12 Homework3

影响相变温度的因素

1. 压力对沸点/凝固点的影响 (Clausius-Clapeyron Equation)

(Slide 14)

• 沸点与压力:
  • 降低压力会降低气相的化学势 ${\mu }_g$。
  • 在 $\mu -T$ 图上，${\mu }_g(T)$ 曲线下移 (或其与 ${\mu }_l(T)$ 的交点左移)。
  • 这导致液-气平衡 (沸腾) 发生在更低的温度。所以高海拔地区水的沸点较低。
  • Slide 14 比较了 1 atm 和 0.8 atm 下水的沸点，结论是 $T_{boil}(0.8\text{ atm})<T_{boil}(1\text{ atm})$。
• 克劳修斯-克拉佩龙方程 (Clausius-Clapeyron Equation) (Slide 14 提及了一个简化形式):
  • 定量描述相界线上压力随温度的变化率： $$\frac{dp}{dT}=\frac{L}{T\mathrm{\Delta }v}=\frac{\mathrm{\Delta }s}{\mathrm{\Delta }v}$$ 其中 $L$ 是相变潜热 (每摩尔或每单位质量)，$\mathrm{\Delta }v$ 是相变过程中的单位粒子体积 (或摩尔体积/比容) 变化，$T$ 是相变温度。
  • Slide 14 给出的 $p=p_0{e}^{-L/kT}$ 是一个积分后的近似形式，通常用于固/液-气相变，假设潜热 $L$ 是常数，且气相体积远大于固/液相体积，并把气体视为理想气体。这里的 $L$ 是单个分子的潜热。

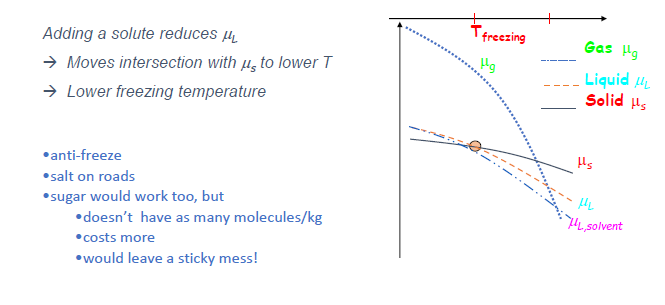
2. 溶质对凝固点/沸点的影响 (依数性)

(Slides 15, 16, 17)

• 基本原理 (Slide 15):
  • 向纯溶剂中溶解非易失性溶质 (solute) 会降低溶剂的化学势 ${\mu }_L$ (即 ${\mu }_{solvent,solution}<{\mu }_{puresolvent}$)。
  • 这是因为溶解过程是自发的，意味着混合态的吉布斯自由能更低。
  • 如果溶质不进入固相或气相，那么 ${\mu }_S$ 和 ${\mu }_G$ (纯溶剂的) 不受影响。
• 凝固点降低 (Freezing point depression) (Slide 16):
  • 由于溶液中溶剂的 ${\mu }_L$ 降低了，其 ${\mu }_L(T)$ 曲线整体下移。
  • 这使得 ${\mu }_L(T)$ 与固相纯溶剂的 ${\mu }_S(T)$ 曲线的交点向更低的温度移动。
  • 因此，溶液的凝固点低于纯溶剂的凝固点。例子：防冻剂、路上撒盐化冰。
• 沸点升高 (Boiling point elevation):
  • 类似地，${\mu }_L(T)$ 曲线下移，导致其与气相纯溶剂的 ${\mu }_G(T)$ 曲线的交点向更高的温度移动。
  • 因此，溶液的沸点高于纯溶剂的沸点 (前提是溶质非易失性)。
• 溶质对溶剂化学势影响的推导 (Slide 17):
  • 假设溶剂 ($L$) 和溶质 ($S$) 形成理想溶液，混合过程的熵变主要是构型熵 (entropy of mixing)。
  • 混合熵 (对于溶剂和溶质的总系统): $S_{mix}=k\ln \frac{(N_L+N_S)!}{N_L!N_S!}$ (这里 $N_L,N_S$ 是溶剂和溶质的粒子数)。
  • 溶剂化学势的变化 $\mathrm{\Delta }{\mu }_L={\mu }_{L,solution}-{\mu }_{L,pure}$。可以通过吉布斯-亥姆霍兹关系或者直接考虑混合自由能得到。
  • Slide 17 用了一个近似的方法来估计 $\mathrm{\Delta }{\mu }_L$ 由于混合熵带来的变化: $\Delta \mu_{L(mix)} = -T \left(\frac{\partial S_{mix}}{\partial N_L}\right){N_S}$(\mathrm{更}\mathrm{准}\mathrm{确}\mathrm{的}\mathrm{应}\mathrm{该}\mathrm{是}\mathrm{考}\mathrm{虑}\mathrm{吉}\mathrm{布}\mathrm{斯}\mathrm{自}\mathrm{由}\mathrm{能}$G{mix} = N_L \mu_{L,pure} + N_S \mu_{S,pure} - T S_{mix}$，\mathrm{然}\mathrm{后}$\mu_{L,solution} = (\partial G_{mix}/\partial N_L)$)。
  • 对于稀溶液 ($N_S\ll N_L$)，利用斯特林近似，可以得到： $$\mathrm{\Delta }{\mu }_L\approx -kT\frac{N_S}{N_L}=-kT{x}_S$$ 其中 $x_S=N_S/(N_L+N_S)\approx N_S/N_L$ 是溶质的摩尔分数。
  • 因为 $x_S>0$，所以 $\mathrm{\Delta }{\mu }_L<0$，即溶剂在溶液中的化学势降低了。

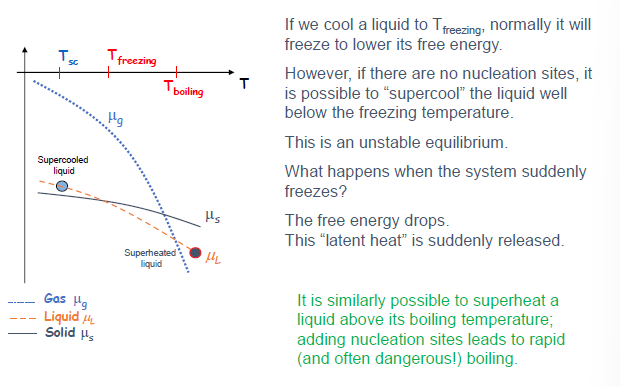
亚稳态：过冷与过热

(Slide 18)

• 过冷 (Supercooling): 将液体冷却到其正常凝固点以下而不发生凝固的现象。
• 过热 (Superheating): 将液体加热到其正常沸点以上而不发生沸腾的现象。
• 原因: 相变通常需要形核点 (nucleation sites) 来启动。如果没有形核点，系统可以暂时处于亚稳态 (unstable equilibrium)。
• 在 $\mu -T$ 图上，亚稳态的相的化学势并不是最低的，但系统被困在这个状态。
• 一旦发生相变 (例如通过引入形核点或扰动)，系统会迅速转变为更稳定的相 (化学势更低的相)，并释放潜热，导致温度可能回升 (过冷液体凝固) 或剧烈沸腾 (过热液体沸腾)。

相变的一般规则

(Slides 19, 21)

• 压力效应: 增加压力有利于体积更小 (即密度更高) 的相。
  • 因为 $(\partial \mu /\partial p{)}_T=v$。压力增大时， $v$ 小的相的 $\mu$ 增加得慢，更容易成为低 $\mu$ 的稳定相。
  • 例如，对于大多数物质 (如氨，Slide 21)，固相密度 > 液相密度 > 气相密度。所以高压有利于固相。水是例外，冰的密度小于水。
• 温度效应: 增加温度有利于熵更大 (即无序度更高) 的相。
  • 因为 $(\partial \mu /\partial T{)}_p=-s$。温度升高时， $s$ 大的相的 $\mu$ 下降得快，更容易成为低 $\mu$ 的稳定相。
  • 通常 $s_{gas}>s_{liquid}>s_{solid}$。所以高温有利于气相。

二元相图 (Binary phase diagrams)

(Slide 23)

• 这是对双组分系统 (如合金) 相平衡的介绍。
• 相图变得更复杂，除了 $T,p$ 外，还有一个变量是成分浓度。
• 图中可能出现共晶点 (Eutectic point)、固溶体 (Solid solution, 如 $\alpha ,\beta$) 等。
• 这部分内容通常在材料科学或更高等的热力学课程中详细讨论，这里只是一个初步的展示，表明相图可以描述更复杂的系统。