The Laplace Transform

#Math285

拉普拉斯变换 (The Laplace Transform)

积分变换与拉普拉斯变换的定义 (Integral Transforms and Definition of Laplace Transform)

• 积分变换 (Integral Transforms)
  • 一般定义: 积分变换是一种数学运算，它将一个函数 $f(t)$ 通过一个积分核函数 $K(s,t)$ 映射到另一个函数 $F(s)$。形式如下： $$F(s)={\int }_a^{b}K(s,t)f(t)dt$$ 这里的 $F(s)$ 是 $f(t)$ 的变换，$s$ 是变换域的变量 (通常是复数)。
• 拉普拉斯变换的定义: 拉普拉斯变换是一种特殊的积分变换，其中积分区间是 $(0,\mathrm{\infty })$，积分核是 $K(s,t)=e^{-st}$。 对于函数 $f(t)$ (定义在 $t\ge 0$)，其拉普拉斯变换 $F(s)$ 或 $\mathcal{L}f(t)$ 定义为： $$F(s)=\mathcal{L}f(t)={\int }_0^{\mathrm{\infty }}{e}^{-st}f(t)dt$$ 这个积分针对所有使得积分收敛的复数 $s$ 进行定义。

拉普拉斯变换的适定域 (An Appropriate Domain for $\mathcal{L}$)

不是所有的函数都有拉普拉斯变换。为了确保积分收敛，函数 $f(t)$ 通常需要满足某些条件：

• 函数的条件
  1. 分段连续 (Piecewise Continuous):
     • (i) 函数 $f(t)$ 的不连续点集 $\mathrm{\Delta }$ 是离散的（即没有极限点）。
     • (ii) $f(t)$ 在不包含不连续点的每个连通区间上是连续的。
     • (iii) 在每个不连续点 $\alpha \in \mathrm{\Delta }$，单侧极限 $f({\alpha }^{+})$ 和 $f({\alpha }^{-})$ 存在。 通俗理解: 函数可以有跳跃间断点，但不能有无穷震荡类型的间断点，且在任何有界区间内只能有有限个跳跃间断点。
  2. 指数阶 (Exponential Order): 函数 $f(t)$ 当 $t\to \mathrm{\infty }$ 时是（至多）指数阶的，如果存在实数 $a$ 和正常数 $K,M$，使得： $$|f(t)|\le K{e}^{at}\text{当 }t\ge M$$ 指数阶意味着函数的增长速度不会超过某个指数函数 $e^{at}$。“指数阶”就像给函数的增长速度设了一个上限，它不能无限快地飞向无穷大。 如果一个函数是分段连续且为指数阶的，那么它的拉普拉斯变换 $\mathcal{L}f(t)$ 是良定义的 (well-defined)，即积分是收敛的（对于某些 $s$ 值）。
• 关于条件的注解
  • 分段连续允许有无限多个跳跃间断点，只要在任何有界子区间 $[0,R]$ 内是有限的 (例如 $f(t)=\lfloor t\rfloor$ 取整函数)。
  • 指数阶 $f(t)=O(e^{at})$ 的条件，其中 $a$ 可以是负数 (意味着函数衰减)。$a$ 越小，对函数增长的限制越强。
  • 精确指数阶 (Exact Exponential Order) $eo(f)$ 定义为使得 $f(t)=O(e^{at})$ 成立的最小的 $a$ 值 (下确界)。 例如，多项式 $t^n$ 的精确指数阶是 $0$，因为对于任何 $a>0$，$t^n=O(e^{at})$，但 $t^n\ne O(e^{0t})=O(1)$ (除非 $n=0$)。
• 指数阶的例子
  1. 非零多项式和有理函数 (分母非零) 的精确指数阶都是 $0$。
  2. 指数多项式 $t\mapsto c_1{e}^{a_{1}t}+\cdots +c_n{e}^{a_{n}t}$ ($a_1<a_2<\cdots <a_n$) 的精确指数阶是 $a_n$ (增长最快的那一项的指数)。
  3. $\sin (at),\cos (at)$ ($a\ne 0$) 的精确指数阶是 $0$ (因为它们是有界的，可以被 $K{e}^{0t}$ 控制)。
  4. $t\mapsto e^{t^2}$ 不是指数阶的，因为它比任何 $e^{at}$ 增长都快。而 $t\mapsto e^{-t^2}$ 的精确指数阶是 $-\mathrm{\infty }$ (因为它比任何 $e^{at}$ 衰减都快)。

拉普拉斯变换的解析性与微分性质 (Analyticity and Differentiation of $F(s)$)

• $F(s)$ 的解析性定理 假设 $f(t)$ 是分段连续的，且精确指数阶为 $a\in \mathbb{R}\cup \pm \mathrm{\infty }$。
  1. 如果 $a=+\mathrm{\infty }$ (如 $e^{t^2}$)，则 $\mathcal{L}f(t)$ 可能对任何 $s$ 都不定义。
  2. 如果 $a\in \mathbb{R}$，则 $\mathcal{L}f(t)$ 至少在开半平面 $\text{Re}(s)>a$ 上有定义且解析 (analytic)。 重要: 解析意味着 $F(s)$ 在该区域内是复可微的，可以展开成幂级数。
  3. 如果 $a=-\mathrm{\infty }$ (如 $e^{-t^2}$)，则 $\mathcal{L}f(t)$ 在整个复平面上都有定义且解析 (即 $F(s)$ 是一个整函数 (entire function))。

  $s$ 域微分性质: 在情况 2 和 3 中，$F(s)=\mathcal{L}f(t)$ 可以在积分号下对 $s$ 微分： $$F^{\prime }(s)=\frac{d}{ds}{\int }_0^{\mathrm{\infty }}{e}^{-st}f(t)dt={\int }_0^{\mathrm{\infty }}\frac{\partial }{\partial s}(e^{-st}f(t))dt={\int }_0^{\mathrm{\infty }}(-t)e^{-st}f(t)dt=-\mathcal{L}tf(t)$$ 推广得到： $$F^{(n)}(s)=(-1{)}^n\mathcal{L}{t}^{n}f(t)$$

• 定理证明概要

  • 证明思路 (Slide 9): 假设 $f(t)$ 是实值的。对于 $\text{Re}(s)\ge a+\delta$ ($\delta >0$)，有 $

    f(t)e^{-st}

    =

    f(t)

    e^{-\text{Re}(s)t} \le K e^{at} e^{-(a+\delta)t} = K e^{-\delta t}$。\mathrm{由}\mathrm{于}$\int_M^\infty K e^{-\delta t} dt$ 收敛，根据魏尔斯特拉斯 M-判别法 (Weierstrass M-test)，积分 ${\int }_0^{\mathrm{\infty }}f(t)e^{-st}dt$ 在 $\text{Re}(s)\ge a+\delta$ 上一致收敛。一致收敛保证了 $F(s)$ 在 $\text{Re}(s)>a$ 上的连续性和可积性。通过证明积分号下微分的条件也满足，可以得到 $F(s)$ 的复可微性，从而得到解析性。

  • 另一种证明思路 (Slide 10): 将 $F(s)=F(x+iy)$ 写成 $u(x,y)+iv(x,y)$ 的形式，然后验证 $u$ 和 $v$ 满足柯西-黎曼方程，从而证明 $F(s)$ 的复可微性（解析性）。

常见函数的拉普拉斯变换示例 (Examples of Laplace Transforms)

• 幻灯片 11:
  1. $\mathcal{L}1={\int }_0^{\mathrm{\infty }}{e}^{-st}\cdot 1dt={[-\frac{1}{s}{e}^{-st}]}_0^{\mathrm{\infty }}=\frac{1}{s}$ (对于 $\text{Re}(s)>0$)
  2. $\mathcal{L}{e}^{at}={\int }_0^{\mathrm{\infty }}{e}^{-st}{e}^{at}dt={\int }_0^{\mathrm{\infty }}{e}^{-(s-a)t}dt=\frac{1}{s-a}$ (对于 $\text{Re}(s)>\text{Re}(a)$)
  3. $\text{Missing or unrecognized delimiter for left}$ (对于 $\text{Re}(s)>0$)
  4. $\text{Missing or unrecognized delimiter for left}$ (对于 $\text{Re}(s)>0$)
• 幻灯片 12:
  1. $\mathcal{L}{t}^n$ (n 为非负整数): $$\mathcal{L}{t}^n={\int }_0^{\mathrm{\infty }}{t}^n{e}^{-st}dt$$ 做替换 $\tau =st$, $d\tau =sdt$: $$={\int }_0^{\mathrm{\infty }}{\left(\frac{\tau }{s}\right)}^n{e}^{-\tau }\frac{d\tau }{s}=\frac{1}{s^{n+1}}{\int }_0^{\mathrm{\infty }}{\tau }^n{e}^{-\tau }d\tau$$ 积分部分是 Gamma 函数 $\mathrm{\Gamma }(n+1)=n!$。 所以 $\mathcal{L}{t}^n=\frac{n!}{s^{n+1}}$ (对于 $\text{Re}(s)>0$)。 更一般地，对于 $r>-1$： $\mathcal{L}{t}^r=\frac{\mathrm{\Gamma }(r+1)}{s^{r+1}}$ (对于 $\text{Re}(s)>0$) 例如 $\mathcal{L}{t}^{-1/2}=\mathcal{L}1/\sqrt{t}=\frac{\mathrm{\Gamma }(1/2)}{s^{1/2}}=\frac{\sqrt{\pi }}{\sqrt{s}}=\sqrt{\frac{\pi }{s}}$。
• 幻灯片 13:
  1. $\mathcal{L}\lfloor t\rfloor$ (向下取整函数, “staircase” function): $\lfloor t\rfloor =n$ 当 $n\le t<n+1$。 $$ \mathcal{L}{\lfloor t \rfloor} = \sum_{n=0}^\infty \int_n^{n+1} n e^{-st} dt = \sum_{n=0}^\infty n \left[-\frac{1}{s}e^{-st}\right]n^{n+1}
     = \sum{n=0}^\infty \frac{n}{s} (e^{-sn} - e^{-s(n+1)}) = \frac{1}{s} \sum_{n=0}^\infty n e^{-sn} (1 - e^{-s}) $$\mathrm{幻}\mathrm{灯}\mathrm{片}\mathrm{中}\mathrm{直}\mathrm{接}\mathrm{给}\mathrm{出}\mathrm{了}\mathrm{结}\mathrm{果}（\mathrm{经}\mathrm{过}\mathrm{级}\mathrm{数}\mathrm{求}\mathrm{和}\mathrm{化}\mathrm{简}）：$$ \mathcal{L}{\lfloor t \rfloor} = \frac{1}{s(e^s-1)} \quad (\text{for Re}(s)>0) $$

拉普拉斯变换的性质 (Properties of Laplace Transform)

• 收敛横坐标 (Abscissa of Convergence)

  • 绝对收敛横坐标 (Abscissa of Absolute Convergence) $\alpha$: 使得 $\int_0^\infty

    f(t)e^{-st}

    dt$\mathrm{收}\mathrm{敛}\mathrm{的}$\text{Re}(s)$\mathrm{的}\mathrm{下}\mathrm{确}\mathrm{界}。\mathrm{积}\mathrm{分}\mathrm{在}$\text{Re}(s) > \alpha$ 时绝对收敛。

  • 收敛横坐标 (Abscissa of Convergence) $\beta$: 使得 ${\int }_0^{\mathrm{\infty }}f(t)e^{-st}dt$ 收敛的 $\text{Re}(s)$ 的下确界。积分在 $\text{Re}(s)>\beta$ 时收敛。
  • 通常 $\beta \le \alpha$。如果 $f(t)$ 的精确指数阶为 $a_{exp}$，则 $\beta \le a_{exp}\le \alpha$。
  • $F(s)$ 在 $\text{Re}(s)>\beta$ 的区域内解析。

• 线性性 (Linearity) 如果 $\mathcal{L}{f}_1(t)$ 在 $\text{Re}(s)>a_1$ 定义，$\mathcal{L}{f}_2(t)$ 在 $\text{Re}(s)>a_2$ 定义，则 $$\mathcal{L}{c}_1{f}_1(t)+c_2{f}_2(t)=c_1\mathcal{L}{f}_1(t)+c_2\mathcal{L}{f}_2(t)$$ 定义域为 $\text{Re}(s)>max{a}_1,a_2$。 这个性质可以直接从积分的线性性得到。 应用: 可以直接计算多项式的拉普拉斯变换，例如 $\mathcal{L}{c}_0+c_{1}t+\cdots +c_d{t}^d=\frac{c_0}{s}+\frac{c_1}{s^2}+\cdots +\frac{c_{d}d!}{s^{d+1}}$。

• 自变量的伸缩 (Dilations in the argument / Scaling) 如果 $F(s)=\mathcal{L}f(t)$，则对于 $r>0$： $$\mathcal{L}f(rt)=\frac{1}{r}F\left(\frac{s}{r}\right)$$ 证明: ${\int }_0^{\mathrm{\infty }}f(rt)e^{-st}dt$。令 $\tau =rt$, $d\tau =rdt$。 $={\int }_0^{\mathrm{\infty }}f(\tau )e^{-s(\tau /r)}\frac{d\tau }{r}=\frac{1}{r}{\int }_0^{\mathrm{\infty }}f(\tau )e^{-(s/r)\tau }d\tau =\frac{1}{r}F\left(\frac{s}{r}\right)$。 例子: $\mathcal{L}\cos (\omega t)=\frac{1}{\omega }\frac{s/\omega }{(s/\omega {)}^2+1}=\frac{s}{s^2+{\omega }^2}$ (已知 $\mathcal{L}\cos t=s/(s^2+1)$)。 $\mathcal{L}\sin (\omega t)=\frac{1}{\omega }\frac{1}{(s/\omega {)}^2+1}=\frac{\omega }{s^2+{\omega }^2}$。 求 $\mathcal{L}{\cos }^{2}t$: 用倍角公式 ${\cos }^{2}t=\frac{1+\cos (2t)}{2}$。 $\mathcal{L}{\cos }^{2}t=\frac{1}{2}(\mathcal{L}1+\mathcal{L}\cos (2t))=\frac{1}{2}(\frac{1}{s}+\frac{s}{s^2+4})=\frac{s^2+2}{s(s^2+4)}$。

• 自变量的平移 (Translations in the argument / Shifting Properties)

  1. $t$ 域平移 ($s$ 域乘以指数) (“Translations in the argument”, 通常称为 第二平移定理 (Second Shifting Theorem) 或 $t$-shifting): 定义单位阶跃函数 (unit step function) $u_c(t)=u(t-c)$: $$u_c(t)=\{\begin{array}{ll}0& t<c\\ 1& t\ge c\end{array}$$ 如果 $F(s)=\mathcal{L}f(t)$，则对于 $c>0$: $$\mathcal{L}{u}_c(t)f(t-c)=e^{-cs}F(s)$$ 技术比喻: $u_c(t)f(t-c)$ 的意思是将原函数 $f(t)$ 向右平移 $c$ 个单位，并且在 $t<c$ 的部分置零。这个操作在 $s$ 域对应于乘以一个指数衰减因子 $e^{-cs}$。 证明: ${\int }_0^{\mathrm{\infty }}{u}_c(t)f(t-c)e^{-st}dt={\int }_c^{\mathrm{\infty }}f(t-c)e^{-st}dt$。令 $\tau =t-c$, $d\tau =dt$。 $={\int }_0^{\mathrm{\infty }}f(\tau )e^{-s(\tau +c)}d\tau =e^{-sc}{\int }_0^{\mathrm{\infty }}f(\tau )e^{-s\tau }d\tau =e^{-sc}F(s)$。 例子: $\mathcal{L}{u}_c(t)=e^{-cs}\mathcal{L}1=\frac{e^{-cs}}{s}$。

  2. $s$ 域平移 ($t$ 域乘以指数) (通常称为 第一平移定理 (First Shifting Theorem) 或 $s$-shifting): 如果 $F(s)=\mathcal{L}f(t)$，则对于任意复数 $c$: $$\mathcal{L}{e}^{ct}f(t)=F(s-c)$$ 技术比喻: 在 $t$ 域乘以一个指数函数 $e^{ct}$，在 $s$ 域对应于将 $F(s)$ 的自变量 $s$ 平移 $c$ 个单位。 例子: $\mathcal{L}{t}^n{e}^{ct}=\frac{n!}{(s-c{)}^{n+1}}$ (已知 $\mathcal{L}{t}^n=n!/s^{n+1}$)。

• 拉普拉斯积分的逐项积分 (Term-wise Integration of Laplace Integrals) 如果一个函数 $f(t)$ 可以表示为收敛的幂级数 $f(t)=\sum _{n=0}^{\mathrm{\infty }}\frac{a_n}{n!}{t}^n$ (即在 $t=0$ 解析)，并且其系数增长满足一定条件，那么它的拉普拉斯变换可以逐项进行： $$\text{Missing or unrecognized delimiter for left}$$ 定理: 若幂级数 $\sum a_n{z}^n$ 的收敛半径为 $R>0$，则对于 $f(t)=\sum _{n=0}^{\mathrm{\infty }}\frac{a_n}{n!}{t}^n$ (对所有 $t\ge 0$ 有定义)，其拉普拉斯变换为 $\mathcal{L}f(t)=\sum _{n=0}^{\mathrm{\infty }}\frac{a_n}{s^{n+1}}$，该级数对于 $\text{Re}(s)>1/R$ 收敛。 例子 (Slide 26-27): 计算 $\text{Missing or unrecognized delimiter for left}$。 已知 $\sin t=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}{t}^{2n+1}$。 所以 $\frac{\sin t}{t}=\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}{t}^{2n}$。(在 $t=0$ 处连续延拓 $f(0)=1$) 这里 $a_{2n}=\frac{(-1{)}^n(2n)!}{(2n+1)!}=\frac{(-1{)}^n}{2n+1}$，奇数项系数为 $0$。 $\text{Missing or unrecognized delimiter for left}$ 这是 $\arctan (1/s)$ 的泰勒展开 (令 $x=1/s$)。所以 $\text{Missing or unrecognized delimiter for left}$ (或 $\text{arccot}(s)$)。

• 拉普拉斯变换与微分 (Laplace Transform and Differentiation)

  1. $s$ 域微分 (Differentiation in the Codomain): $$F^{\prime }(s)=-\mathcal{L}tf(t)\text{or}\mathcal{L}tf(t)=-F^{\prime }(s)$$ 例子: 推导 $\mathcal{L}{t}^k{e}^{ct}$。已知 $\mathcal{L}{e}^{ct}=\frac{1}{s-c}$。 $\mathcal{L}t{e}^{ct}=-\frac{d}{ds}\left(\frac{1}{s-c}\right)=\frac{1}{(s-c{)}^2}$。 $\mathcal{L}{t}^2{e}^{ct}=-\frac{d}{ds}\left(\frac{1}{(s-c{)}^2}\right)=\frac{2}{(s-c{)}^3}$。 依此类推 $\mathcal{L}{t}^k{e}^{ct}=\frac{k!}{(s-c{)}^{k+1}}$。

  2. $t$ 域微分 (Differentiation in the Domain): 这是将拉普拉斯变换应用于求解微分方程的核心。 定理: 假设 $f(t)$ 连续且 $f^{\prime }(t)$ 分段连续，且 $\mathcal{L}f(t)=F(s)$ 在 $\text{Re}(s)>a$ 定义。则： $$\mathcal{L}{f}^{\prime }(t)=sF(s)-f(0)(\text{for Re}(s)>a)$$ 如果 $f(0)$ 不连续，用 $f(0^{+})$ 代替。 证明思路: 分部积分 ${\int }_0^{\mathrm{\infty }}{f}^{\prime }(t)e^{-st}dt=[f(t)e^{-st}{]}_0^{\mathrm{\infty }}-{\int }_0^{\mathrm{\infty }}f(t)(-s{e}^{-st})dt=(0-f(0))+s{\int }_0^{\mathrm{\infty }}f(t)e^{-st}dt=sF(s)-f(0)$。 这里需要 $f(t)e^{-st}\to 0$ 当 $t\to \mathrm{\infty }$，这由 $f(t)$ 的指数阶和 $\text{Re}(s)>a$ 保证。

     推论 (Corollary): 对于高阶导数 (假设 $f,f^{\prime },\dots ,f^{(n-1)}$ 连续，$f^{(n)}$ 分段连续)： $$\mathcal{L}{f}^{(n)}(t)=s^{n}F(s)-s^{n-1}f(0)-s^{n-2}{f}^{\prime }(0)-\cdots -f^{(n-1)}(0)$$ $t$ 域的微分运算在 $s$ 域对应于乘以 $s$ 并减去初始条件相关的项。这正是它能将微分方程转化为代数方程的魔力所在。

• 拉普拉斯变换与积分 (Laplace Transform and Integration)

  1. $t$ 域积分 (Integration in the Domain): 如果 $F(s)=\mathcal{L}f(t)$，则 $$\text{Missing or unrecognized delimiter for left}$$ 证明思路: 令 $g(t)={\int }_0^{t}f(\tau )d\tau$。则 $g^{\prime }(t)=f(t)$ 且 $g(0)=0$。 $\mathcal{L}{g}^{\prime }(t)=s\mathcal{L}g(t)-g(0)\Rightarrow \mathcal{L}f(t)=s\mathcal{L}g(t)\Rightarrow F(s)=s\mathcal{L}g(t)$。 所以 $\mathcal{L}g(t)=F(s)/s$。

  2. $s$ 域积分 (Integration in the Codomain) 如果 $\mathcal{L}f(t)=F(s)$ 且 $\underset{t\to 0^{+}}{lim}\frac{f(t)}{t}$ 存在 (或更一般地，${\int }_0^1\frac{f(t)}{t}dt$ 存在)，则： $$\text{Missing or unrecognized delimiter for left}$$ 例子: 已知 $\mathcal{L}\sin t=\frac{1}{s^2+1}$。 $\text{Missing or unrecognized delimiter for left}$ (与之前逐项积分结果一致)。 再用 $t$ 域积分性质：$\text{Missing or unrecognized delimiter for left}$。 ${\int }_0^t\frac{\sin \tau }{\tau }d\tau$ 被称为正弦积分 (Sine Integral) $\text{Si}(t)$。

• 拉普拉斯变换与卷积 (Laplace Transform and Convolution) 卷积定义: 两个函数 $f(t)$ 和 $g(t)$ (定义在 $t\ge 0$) 的卷积 $(fg)(t)$\mathrm{定}\mathrm{义}\mathrm{为}：$$ (fg)(t) = \int_0^t f(\tau) g(t-\tau) d\tau $$ 卷积定理 (Convolution Theorem): 如果 $\mathcal{L}f(t)=F(s)$ 且 $\mathcal{L}g(t)=G(s)$，则： $$ \mathcal{L}{(fg)(t)} = F(s)G(s) $$ 即，$t$ 域的卷积对应于 $s$ 域的普通乘积。 证明思路 (Slide 38, 40-41): 从 $F(s)G(s)$ 的定义出发，将其写成二重积分，然后通过变量替换（令 $u=t_1+\tau ,v=t_1$ 或类似的）和交换积分次序 (需要 Fubini 定理保证) 得到 $\mathcal{L}{(fg)(t)}$ 的形式。 应用 (Slide 42): 求 $\text{Missing or unrecognized delimiter for left}$。 $\frac{s}{(s^2+1{)}^2}=\frac{s}{s^2+1}\cdot \frac{1}{s^2+1}$。 已知 $\mathcal{L}\cos t=\frac{s}{s^2+1}$ 且 $\mathcal{L}\sin t=\frac{1}{s^2+1}$。 所以 $\text{Missing or unrecognized delimiter for left}$。 通过三角恒等式计算积分得到 $\frac{1}{2}t\sin t$。 所以 $\text{Missing or unrecognized delimiter for left}$。

拉普拉斯逆变换 (Inversion of the Laplace Transform)

• 唯一性 (Uniqueness): 如果两个分段连续函数 $f_1(t)$ 和 $f_2(t)$ 具有相同的拉普拉斯变换 $F(s)$，那么它们在所有连续点上是相等的。也就是说，拉普拉斯逆变换 ${\mathcal{L}}^{-1}F(s)$ (在连续点上) 是唯一的。 更准确地说，如果 $F_1(s)=F_2(s)$ 在某个右半平面成立，并且满足一定条件，则 $f_1(t^{-})=f_2(t^{-})$ 且 $f_1(t^{+})=f_2(t^{+})$。如果 $f_1,f_2$ 连续，则 $f_1=f_2$。
• 逆变换公式（不考）: 存在一个明确的逆变换公式，称为Bromwich 积分或 Mellin 逆变换公式，它涉及到复平面上的路径积分： $$f(t)=\frac{1}{2\pi i}\underset{T\to \mathrm{\infty }}{lim}{\int }_{\gamma -iT}^{\gamma +iT}{e}^{st}F(s)ds$$ 其中 $\gamma$ 是一个实数，使得积分路径在 $F(s)$ 的所有奇点右侧。这个公式在实际计算中通常与留数定理结合使用，超出了本课程的基础范围。 在实践中，我们通常通过查表和利用拉普拉斯变换的性质来求逆变换。

用拉普拉斯变换求解初值问题 (IVP)

Basic Idea

这是拉普拉斯变换在微分方程中的核心应用。

核心变换方程 $$\mathcal{L}{f}^{(n)}(t)=s^{n}F(s)-s^{n-1}f(0)-s^{n-2}{f}^{\prime }(0)-\cdots -f^{(n-1)}(0)$$

• 基本思想: 对于一个常系数线性微分方程的初值问题，例如二阶： $a{y}^{″}+b{y}^{\prime }+cy=f(t)$, $y(0)=y_0$, $y^{\prime }(0)=y_1$ 求解步骤：
  1. 变换方程: 对整个微分方程两边取拉普拉斯变换。利用微分性质 $\mathcal{L}{y}^{\prime }(t)=sY(s)-y(0)$ 和 $\mathcal{L}{y}^{\prime }‘(t)=s^{2}Y(s)-sy(0)-y^{\prime }(0)$ (其中 $Y(s)=\mathcal{L}y(t)$), 以及右端项 $f(t)$ 的变换 $F_s(s)=\mathcal{L}f(t)$。这将把微分方程转换成一个关于 $Y(s)$ 的代数方程。
  2. 求解 $Y(s)$: 从代数方程中解出 $Y(s)$。
  3. 逆变换: 对 $Y(s)$ 进行拉普拉斯逆变换得到原函数 $y(t)={\mathcal{L}}^{-1}Y(s)$。这通常需要部分分式分解 (partial fraction decomposition) 和查表。
• 例子: $y^{\prime }+2y=-1$, $y(0)=1$
  1. $\mathcal{L}{y}^{\prime }+2\mathcal{L}y=\mathcal{L}-1$ $(sY(s)-y(0))+2Y(s)=-1/s$ $sY(s)-1+2Y(s)=-1/s$
  2. $(s+2)Y(s)=1-1/s=(s-1)/s$ $Y(s)=\frac{s-1}{s(s+2)}$
  3. 部分分式: $\frac{s-1}{s(s+2)}=\frac{A}{s}+\frac{B}{s+2}$。解得 $A=-1/2,B=3/2$。 $Y(s)=-\frac{1}{2s}+\frac{3}{2(s+2)}$ $\text{Missing or unrecognized delimiter for left}$
• 例子: $y^{″}+y=\sin (\omega t)$, $y(0)=1,y^{\prime }(0)=1$
  1. $\mathcal{L}{y}^{″}+\mathcal{L}y=\mathcal{L}\sin (\omega t)$ $(s^{2}Y(s)-sy(0)-y^{\prime }(0))+Y(s)=\frac{\omega }{s^2+{\omega }^2}$ $s^{2}Y(s)-s-1+Y(s)=\frac{\omega }{s^2+{\omega }^2}$
  2. $(s^2+1)Y(s)=s+1+\frac{\omega }{s^2+{\omega }^2}$ $Y(s)=\frac{s+1}{s^2+1}+\frac{\omega }{(s^2+1)(s^2+{\omega }^2)}$

  3. Case $\omega \ne \pm 1$: $\frac{\omega }{(s^2+1)(s^2+{\omega }^2)}=\frac{As+B}{s^2+1}+\frac{Cs+D}{s^2+{\omega }^2}$。 幻灯片直接给出分解结果（或通过特定技巧）： $\frac{\omega }{(s^2+1)(s^2+{\omega }^2)}=\frac{\omega }{{\omega }^2-1}(\frac{1}{s^2+1}-\frac{1}{s^2+{\omega }^2})$。 $Y(s)=\frac{s}{s^2+1}+\frac{1}{s^2+1}+\frac{\omega }{{\omega }^2-1}\frac{1}{s^2+1}-\frac{\omega }{{\omega }^2-1}\frac{1}{s^2+{\omega }^2}$ $Y(s)=\frac{s}{s^2+1}+(1+\frac{\omega }{{\omega }^2-1})\frac{1}{s^2+1}-\frac{1}{{\omega }^2-1}\frac{\omega }{s^2+{\omega }^2}$ $Y(s)=\frac{s}{s^2+1}+\frac{{\omega }^2+\omega -1}{{\omega }^2-1}\frac{1}{s^2+1}-\frac{1}{{\omega }^2-1}\frac{\omega }{s^2+{\omega }^2}$ $y(t)=\cos t+\frac{{\omega }^2+\omega -1}{{\omega }^2-1}\sin t-\frac{1}{{\omega }^2-1}\sin (\omega t)$

  4. Case $\omega =\pm 1$: (共振情况) 如果 $\omega =1$, $Y(s)=\frac{s+1}{s^2+1}+\frac{1}{(s^2+1{)}^2}$。 $\text{Missing or unrecognized delimiter for left}$。 需要求 $\text{Missing or unrecognized delimiter for left}$。

Continuous Forcing & Discontinuous Forcing

我们考虑一个典型的二阶常系数线性微分方程： $$a{y}^{″}+b{y}^{\prime }+cy=f(t)$$ 其中 $a,b,c$ 是常数，$a\ne 0$，而 $f(t)$ 就是所谓的强迫项 (forcing function) 或输入函数。

1. 连续强迫项 (Continuous Forcing)

定义与含义

当强迫项 $f(t)$ 在所考虑的时间区间（通常是 $t\ge 0$）上是一个连续函数时，我们称之为连续强迫。这意味着 $f(t)$ 的图像没有断裂或跳跃。

例子:

• $f(t)=-1$ (常数函数，Slide 47)
• $f(t)=\sin (\omega t)$ (正弦函数，Slide 48)
• $f(t)=e^{kt}$ (指数函数)
• $f(t)=t^2$ (多项式函数)
• Slide 62 中的分段函数，虽然是分段定义的，但它在连接点 $t=1$ 处是连续的 ($t=1$ 时 $f(1)=1$；$2-t$ 在 $t=1$ 时 $f(1)=1$)，所以它仍然是一个连续强迫项。

对解的影响和处理方法

1. 解的存在唯一性 (Slide 51): 如果 $f(t)$ 是连续的，那么根据常微分方程的存在唯一性定理 (Existence and Uniqueness Theorem) (对于线性方程有更强的结论)，对于给定的初始条件 $y(0)=y_0,y^{\prime }(0)=y_1$，微分方程在 $t\ge 0$ 上存在唯一的解 $y(t)$。这个解 $y(t)$ 本身以及它的导数 $y^{\prime }(t)$ 和二阶导数 $y^{\prime }‘(t)$ 都会是连续的。

2. 求解方法:
   • 待定系数法 (Method of Undetermined Coefficients): 如果 $f(t)$ 是特定形式的函数（如多项式、指数函数、正弦/余弦函数及其乘积和线性组合），此方法适用。
   • 参数变易法 (Variation of Parameters): 这是一个更通用的方法，适用于任何连续的 $f(t)$。
   • 拉普拉斯变换法 (Laplace Transform Method): 这种方法对于连续强迫项同样有效。
3. 解的性质 (Slide 52Theorem): 如果 $f(t)$ 是连续且指数阶的，那么任何解 $y(t)$ 也是连续且指数阶的。这意味着解 $y(t)$ 的拉普拉斯变换 $Y(s)$ 存在于某个右半平面。

2. 不连续强迫项 (Discontinuous Forcing) (Slides 53-61, 64-70)

定义与含义

当强迫项 $f(t)$ 在所考虑的时间区间上不是处处连续时，我们称之为不连续强迫。最常见的不连续类型是跳跃间断点 (jump discontinuities)。这意味着 $f(t)$ 的图像在某些点会发生突然的跳跃。

例子:

• 阶梯函数/矩形脉冲 (Slide 53, 57-59): $f(t)=\{\begin{array}{ll}1& 0<t<1\\ 0& t>1\end{array}$ 这个函数在 $t=1$ 处有一个跳跃间断点。
• 一系列矩形脉冲 (Slide 60-61): $f(t)=1$ for $t\in [0,1]\cup [2,3]\cup [4,5]$, and $0$ otherwise. 这个函数在 $t=1,2,3,4,5$ 都有跳跃间断点。
• 脉冲函数 (Impulsive Forcing - 狄拉克 $\delta$ 函数, Slides 64-70): 狄拉克 $\delta$ 函数是一种理想化的不连续强迫，它在单个点上施加一个“无穷大”的力，但在极短的时间内完成，使得总冲量为有限值 (通常为1)。这是一种极端的不连续。

对解的影响和处理方法

1. 解的定义调整 (Slide 53 Definition): 当 $f(t)$ 不连续时，$y^{\prime }‘(t)$ 通常在 $f(t)$ 的不连续点处不存在 (因为 $y^{\prime }‘(t)=(f(t)-b{y}^{\prime }-cy)/a$，如果 $f(t)$ 跳跃，$y^{\prime },y$ 连续，则 $y^{″}$ 也会跳跃，从而导致 $y^{″}$ 不存在)。 因此，我们需要调整对“解”的定义：
   • 一个函数 $y(t)$ 称为 IVP 的解，如果：
     1. $y(t)$ 是 $C^1$ 函数，即 $y(t)$ 和 $y^{\prime }(t)$ 都是连续的。这是非常重要的一点！即使强迫项不连续，解本身和它的一阶导数通常仍然保持连续性。 这源于物理系统的惯性，例如一个物体的位置和速度不会因为受到的力突然改变而瞬间跳变。
     2. $y^{\prime }‘(t)$ 存在于 $f(t)$ 连续的那些点，并且在这些点上满足微分方程 $a{y}^{″}+b{y}^{\prime }+cy=f(t)$。
     3. $y(t)$ 满足初始条件 $y(0)=y_0,y^{\prime }(0)=y_1$。
2. 解的存在唯一性 (Slide 55 Theorem):
   • 如果 $f(t)$ 是分段连续的，则 IVP 仍然具有唯一的解 (在上述调整的定义下)。
   • 这个唯一的解可以通过以下方式构造：在 $f(t)$ 的每个连续区间内分别求解 ODE，并利用 $y(t)$ 和 $y^{\prime }(t)$ 的连续性在间断点处“粘合”这些解段。
3. 求解方法:
   • 拉普拉斯变换法 (Laplace Transform Method): 这是处理不连续强迫项非常强大和方便的方法。利用单位阶跃函数与拉普拉斯变换的平移性质与线性，我们可以轻松解决非连续的情况
     • 关键在于能够将分段定义的 $f(t)$ 用单位阶跃函数 $u_c(t)$ 表示出来。 例如，$f(t)=\{\begin{array}{ll}{g}_1(t)& 0\le t<c\\ g_2(t)& t\ge c\end{array}$ 可以写成 $f(t)=g_1(t)+u_c(t)(g_2(t)-g_1(t))$ (如果 $g_1(t)$ 在 $t\ge c$ 也有定义且我们想在 $t\ge c$ 时完全替换为 $g_2(t)$)，或者更常见的是用 $f(t)=g_1(t)[u_0(t)-u_c(t)]+g_2(t)u_c(t)$ 这样的形式。 对于矩形脉冲 $f(t)=1$ for $a\le t<b$ and $0$ 否则，可以表示为 $f(t)=u_a(t)-u_b(t)$。
     • 一旦 $f(t)$ 用单位阶跃函数表示，就可以利用拉普拉斯变换的第二平移定理 ($\mathcal{L}{u}_c(t)g(t-c)=e^{-cs}G(s)$) 来求 $\mathcal{L}f(t)$。
     • 后续步骤与连续强迫项类似：解出 $Y(s)$，然后进行逆变换。逆变换时也可能需要用到第二平移定理。
4. 解的性质:
   • $y(t)$ 和 $y^{\prime }(t)$ 是连续的。
   • $y^{\prime }‘(t)$ 在 $f(t)$ 的不连续点处通常也是不连续的（发生跳跃）。这意味着解的“平滑度”降低了，但不会像 $f(t)$ 那样完全断开。
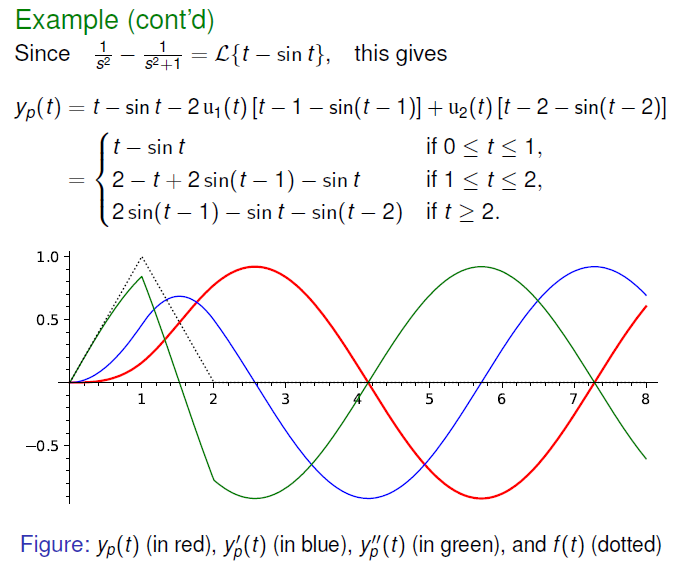
   • 例子 (Slide 59 图像):
     • 强迫项 $f(t)$ (虚线) 在 $t=1$ 处从 $1$ 跳到 $0$。
     • 解 $y(t)$ (红色曲线) 在 $t=1$ 处是连续的，并且其斜率 $y^{\prime }(t)$ (蓝色曲线) 在 $t=1$ 处也是连续的。
     • 但是，如果观察 $y^{\prime }(t)$ 的斜率 (即 $y^{\prime }‘(t)$)，你会发现在 $t=1$ 处，$y^{\prime }(t)$ 的变化趋势有一个急剧的转折，这意味着 $y^{\prime }‘(t)$ 在那里不连续。
     • 在 $0<t<1$ 区间，ODE 是 $y^{\prime }‘+y=1$。在 $t>1$ 区间，ODE 是 $y^{\prime }‘+y=0$。解在这两个区间内分别满足对应的方程。

例题

• 注意如何将时域与频域的平移相互对应
• 注意如何将分段函数利用 $u(t)$ 进行转化

针对脉冲强迫 (Impulsive Forcing - Dirac $\delta$ Function)

脉冲强迫的核心性质 $$\begin{array}{rlrlrl}& \mathcal{L}(\delta (t))=1& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t)dt=1& {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(t)\delta (t-t_0)dt=\frac{f(t_0-)+f(t_0+)}{2}& \mathcal{L}(\delta (t-t_0))=e^{-s{t}_0}& u^{\prime }(t)=\delta (t)\end{array}$$

这是不连续强迫的一种极端情况。

• 影响: 当强迫项是 $\delta (t-t_0)$ 时，它在 $t=t_0$ 时刻给系统一个瞬时冲量。
  • 解 $y(t)$ 在 $t=t_0$ 处仍然是连续的。
  • 但是，解的一阶导数 $y^{\prime }(t)$ 在 $t=t_0$ 处会发生一个跳跃。跳跃的幅度与 $\delta$ 函数的系数和 $y^{″}$ 项的系数有关。 例如，对于 $a{y}^{\prime }‘+b{y}^{\prime }+cy=k\delta (t-t_0)$，如果 $y(t_0^{-})$ 和 $y^{\prime }(t_0^{-})$ 是 $t_0$ 之前的状态，则 $y(t_0^{+})=y(t_0^{-})$，但 $y^{\prime }(t_0^{+})-y^{\prime }(t_0^{-})=k/a$。
  • $y^{\prime }‘(t)$ 则会包含一个 $\delta$ 函数项。

• 求解: 拉普拉斯变换是处理 $\delta$ 函数强迫项的标准且有效的方法，因为 $\mathcal{L}\delta (t-t_0)=e^{-s{t}_0}$ 形式简单。

• 卷积的应用 (Slide 71: The use of the convolution) 对于 $a{Y}^{″}+b{Y}^{\prime }+cY=F_s(s)$ (假设初始条件为0，得到特解 $Y_p(s)$)， $Y_p(s)=\frac{1}{a{s}^2+bs+c}{F}_s(s)=H(s)F_s(s)$。 $H(s)=\frac{1}{a{s}^2+bs+c}$ 称为系统的传递函数 (transfer function)。 $h(t)={\mathcal{L}}^{-1}H(s)$ 称为系统的脉冲响应 (impulse response)，即当输入为 $\delta (t)$ (单位脉冲) 时的输出。 根据卷积定理，$y_p(t)=(h\ast f)(t)={\int }_0^{t}h(t-\tau )f(\tau )d\tau$。 即，系统的零状态响应是脉冲响应与输入信号的卷积。