Series Solutions of Ordinary Differential Equations

#Math285

引言 (Introduction)

我们已经学习了一些求解特定类型微分方程的方法，例如一阶线性方程、变量分离方程以及常系数线性方程等。然而，许多重要的微分方程，特别是那些来源于物理和工程问题的方程 (例如带有非恒定系数的二阶线性方程)，不能用这些初等方法求解。

本部分的核心目标是引入一种强大的分析工具——幂级数 (Power Series)，来寻找更广泛类型的微分方程的解，特别是解析解 (Analytic Solutions)。

我们将首先回顾幂级数和解析函数的基本性质，这是理解后续方法的基石。然后，我们将重点讨论如何利用幂级数求解二阶线性 ODEs。我们会区分两种情况：在常点 (Ordinary Points) 附近求解和在正则奇点 (Regular Singular Points) 附近求解。后者将引出重要的 Frobenius 方法 (Method of Frobenius)。

幂级数与解析函数 (Power Series and Analytic Functions)

解析解的定义 (Definition of Analytic Solution)

一个标量 ODE 的解析解 (Analytic Solution) 或幂级数解 (Power Series Solution) 是指一个可以用幂级数表示的函数： $$y(t)=\sum _{n=0}^{\mathrm{\infty }}{a}_n(t-t_0{)}^n,t\in I$$ 其中 $I$ 是一个包含中心点 $t_0$ 且长度大于零的区间。

• 这个名称来源于解析函数 (Analytic Function)。一个函数 $f:D\to \mathbb{C}$ ($D\subseteq \mathbb{C}$) 如果在其定义域 $D$ 内的每一点 $z_0$ 的邻域内都可以表示为收敛的幂级数 $f(z)=\sum _{n=0}^{\mathrm{\infty }}{a}_n(z-z_0{)}^n$，则称 $f$ 在 $D$ 上是解析的 (或称为全纯的 (Holomorphic))。实值函数 $f:D\to \mathbb{R}$ ($D\subseteq \mathbb{R}$) 的解析性定义类似。
• 解存在的区间 $I$ 必须包含在幂级数的收敛区间 (Interval of Convergence) 内。这个区间形式为 $(t_0-\rho ,t_0+\rho )$，其中 $\rho$ 是收敛半径 (Radius of Convergence)，且 $\rho >0$。

解析函数的存在唯一性定理 (Existence and Uniqueness Theorem - Analytic Version)

• 定理 (非正式)：对于初值问题 (IVP) $y^{(n)}=f(t,y,y^{\prime },\dots ,y^{(n-1)})$，如果函数 $f$ 关于其所有变量在点 $(t_0,c_0,c_1,\dots ,c_{n-1})$ 附近是解析的，那么该 IVP 的解 $y(t)$ 在 $t_0$ 附近也是解析的，并且在解有定义的区域内满足 ODE。
• 这个定理是使用幂级数方法求解 ODE 的理论基础。它保证了如果 ODE 的系数和非齐次项 (如果存在) 是解析的，那么其解也是解析的，因此我们可以尝试用幂级数形式 $y(x)=\sum a_n(x-x_0{)}^n$ 来寻找解，这种方法称为 幂级数 Ansatz (Power Series Ansatz)。”Ansatz” 是德语，意为 “设定” 或 “尝试”。

Example

示例：求解 IVP $y^{\prime }=x^2+y^2,y(0)=1$

(对应 Slides 7-9)

这是一个非线性 ODE，但右侧 $f(x,y)=x^2+y^2$ 是关于 $x$ 和 $y$ 的多项式，因此是解析函数。定理保证解在 $x=0$ 附近是解析的。

• 方法 1：通过 ODE 确定 $y^{(n)}(0)$
  1. 我们知道 $y(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n$ 的系数由 $a_n=\frac{y^{(n)}(0)}{n!}$ 给出。
  2. $y(0)=1$ 给出 $a_0=1$。
  3. $y^{\prime }(x)=x^2+y^2⟹y^{\prime }(0)=0^2+y(0{)}^2=1^2=1$。所以 $a_1=1/1!=1$。
  4. $y^{\prime }‘(x)=\frac{d}{dx}(x^2+y^2)=2x+2y{y}^{\prime }⟹y^{\prime }‘(0)=2(0)+2y(0)y^{\prime }(0)=2(1)(1)=2$。所以 $a_2=2/2!=1$。
  5. $y^{″}‘(x)=\frac{d}{dx}(2x+2y{y}^{\prime })=2+2(y^{\prime }{)}^2+2y{y}^{″}⟹y^{″}‘(0)=2+2(y^{\prime }(0){)}^2+2y(0)y^{\prime }‘(0)=2+2(1{)}^2+2(1)(2)=8$。所以 $a_3=8/3!=4/3$。
  6. $y^{(4)}(x)=\frac{d}{dx}(2+2(y^{\prime }{)}^2+2y{y}^{″})=4y^{\prime }{y}^{″}+2y^{\prime }{y}^{″}+2y{y}^{‴}=6y^{\prime }{y}^{″}+2y{y}^{‴}⟹y^{(4)}(0)=6y^{\prime }(0)y^{\prime }‘(0)+2y(0)y^{″}‘(0)=6(1)(2)+2(1)(8)=12+16=28$。所以 $a_4=28/4!=28/24=7/6$。
  7. 解为 $y(x)=1+x+x^2+\frac{4}{3}{x}^3+\frac{7}{6}{x}^4+\dots$
     • 缺点：计算高阶导数非常繁琐，且无法直接得到收敛半径信息。
• 方法 2：代入级数并比较系数
  1. 设 $y(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n$。那么 $y^{\prime }(x)=\sum _{n=1}^{\mathrm{\infty }}n{a}_n{x}^{n-1}=\sum _{k=0}^{\mathrm{\infty }}(k+1)a_{k+1}{x}^k$ (令 $k=n-1$)。
  2. $y(x{)}^2=(\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n)(\sum _{m=0}^{\mathrm{\infty }}{a}_m{x}^m)=\sum _{n=0}^{\mathrm{\infty }}(\sum _{k=0}^n{a}_k{a}_{n-k})x^n$ (Cauchy 乘积)。
  3. 代入 ODE：$\sum _{n=0}^{\mathrm{\infty }}(n+1)a_{n+1}{x}^n=x^2+\sum _{n=0}^{\mathrm{\infty }}(\sum _{k=0}^n{a}_k{a}_{n-k})x^n$。
  4. 比较 $x^n$ 的系数：
     • $n=0$: $(0+1)a_1=\sum _{k=0}^0{a}_k{a}_{0-k}=a_0{a}_0=a_0^2$。因为 $a_0=y(0)=1$，所以 $a_1=1^2=1$。
     • $n=1$: $(1+1)a_2=\sum _{k=0}^1{a}_k{a}_{1-k}=a_0{a}_1+a_1{a}_0=2a_0{a}_1=2(1)(1)=2$。所以 $a_2=1$。
     • $n=2$: $(2+1)a_3=1+\sum _{k=0}^2{a}_k{a}_{2-k}=1+(a_0{a}_2+a_1{a}_1+a_2{a}_0)=1+(1)(1)+(1)(1)+(1)(1)=4$。所以 $a_3=4/3$。
     • $n\ge 3$: $(n+1)a_{n+1}=\sum _{k=0}^n{a}_k{a}_{n-k}$。
  5. 这个递推关系 (Recursion Formula) 可以用来计算任意 $a_n$，并且结果与方法 1 一致。
• 收敛半径 (Radius of Convergence)
  • 由于 $a_0=1,a_1=1$，且递推公式只涉及正项和加法，易知所有 $a_n>0$ for $n\ge 0$。
  • 归纳证明 $a_n\ge 1$ for all $n\ge 0$ 。

  • 如果 $a_n\ge 1$，那么 $\lim_{n\to\infty}

    a_n x^n

    = \infty$if$

    x

    1$。\mathrm{因}\mathrm{此}\mathrm{级}\mathrm{数}\mathrm{在}$

    x

    1$\mathrm{发}\mathrm{散}，\mathrm{所}\mathrm{以}\mathrm{收}\mathrm{敛}\mathrm{半}\mathrm{径}$\rho \le 1$。

  • 反过来，假设 $a_k\le c^k$ 对所有 $k<n$ 成立 (对于某个 $c\ge 1$)。那么 $a_n$ 可以被 $c^n$ 界定吗？ $(n+1)a_{n+1}=\sum _{k=0}^n{a}_k{a}_{n-k}+{\delta }_{n,2}$。 如果 $n\ge 3$， $(n+1)a_{n+1}=\sum _{k=0}^n{a}_k{a}_{n-k}\le \sum _{k=0}^n{c}^k{c}^{n-k}=\sum _{k=0}^n{c}^n=(n+1)c^n$。 所以 $a_{n+1}\le c^n$。则我们有 $a_n\le c^n$, 结合级数收敛的要求可以估计 $\rho \ge \frac{1}{c}$

示例：求解 $y^{\prime }=y^2$

• 这是一个可分离变量方程，易解得 $y(x)=1/(C-x)$。
• 使用幂级数 Ansatz $y(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n$ (中心 $x_0=0$)。
• 递推关系变为 $(n+1)a_{n+1}=\sum _{k=0}^n{a}_k{a}_{n-k}$。
• 设 $a_0$ 为任意常数 (对应初值 $y(0)=a_0$)。
• $a_1=a_0^2$
• $2a_2=a_0{a}_1+a_1{a}_0=2a_0(a_0^2)=2a_0^3⟹a_2=a_0^3$
• $3a_3=a_0{a}_2+a_1{a}_1+a_2{a}_0=a_0(a_0^3)+(a_0^2)(a_0^2)+(a_0^3)a_0=3a_0^4⟹a_3=a_0^4$
• 归纳可证 $a_n=a_0^{n+1}$。
• 所以 $y(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_0^{n+1}{x}^n=a_0\sum _{n=0}^{\mathrm{\infty }}(a_{0}x{)}^n$。

• 这是公比为 $a_{0}x$ 的几何级数，当 $

  a_0 x

  < 1$\mathrm{时}\mathrm{收}\mathrm{敛}，\mathrm{和}\mathrm{为}$y(x) = a_0 \frac{1}{1 - a_0 x} = \frac{a_0}{1 - a_0 x}$。

• 令 $C=1/a_0$，则 $y(x)=\frac{1/C}{1-x/C}=\frac{1}{C-x}$。

• 收敛半径 $\rho = 1/

  a_0

  =

  C

  $。\mathrm{这}\mathrm{与}\mathrm{我}\mathrm{们}\mathrm{已}\mathrm{知}\mathrm{解}$y=1/(C-x)$\mathrm{在}$x=C$ 处有奇点相符。

• 注意：幂级数解只在收敛区间 $

  x

  < \rho = 1/

  a_0

  $\mathrm{内}\mathrm{有}\mathrm{效}，\mathrm{而}\mathrm{解}$y=1/(C-x)$\mathrm{本}\mathrm{身}\mathrm{可}\mathrm{能}\mathrm{在}\mathrm{更}\mathrm{大}\mathrm{的}\mathrm{区}\mathrm{间}(\mathrm{例}\mathrm{如}$(-\infty, C)$\mathrm{或}$(C, \infty)$)\mathrm{上}\mathrm{有}\mathrm{定}\mathrm{义}。\mathrm{幂}\mathrm{级}\mathrm{数}\mathrm{只}\mathrm{给}\mathrm{出}\mathrm{了}\mathrm{包}\mathrm{含}\mathrm{中}\mathrm{心}\mathrm{点}$x_0=0$ 的那部分解。

示例：两个类 Euler 方程

(对应 Slides 12-13)

• (E1) $x{y}^{″}+y^{\prime }+y=0$
• (E2) $x^2{y}^{″}+y^{\prime }+y=0$ 两者在 $x=0$ 处都有奇点。
• 使用幂级数 Ansatz $y(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n$。
• 需要 $y^{\prime }(x)=\sum _{n=1}^{\mathrm{\infty }}n{a}_n{x}^{n-1}$ 和 $y^{\prime }‘(x)=\sum _{n=2}^{\mathrm{\infty }}n(n-1)a_n{x}^{n-2}$。
• 对于 (E1):
  • $x{y}^{″}=\sum _{n=2}^{\mathrm{\infty }}n(n-1)a_n{x}^{n-1}=\sum _{k=1}^{\mathrm{\infty }}(k+1)k{a}_{k+1}{x}^k$ (令 $k=n-1$)
  • $y^{\prime }=\sum _{n=1}^{\mathrm{\infty }}n{a}_n{x}^{n-1}=a_1+\sum _{k=1}^{\mathrm{\infty }}(k+1)a_{k+1}{x}^k$ (令 $k=n-1$)
  • $y=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n=a_0+\sum _{k=1}^{\mathrm{\infty }}{a}_k{x}^k$
  • 代入 ODE: $a_1+a_0+\sum _{k=1}^{\mathrm{\infty }}[(k+1)k{a}_{k+1}+(k+1)a_{k+1}+a_k]x^k=0$
  • 常数项：$a_1+a_0=0⟹a_1=-a_0$。
  • $x^k$ 系数 ($k\ge 1$)：$(k+1{)}^2{a}_{k+1}+a_k=0⟹a_{k+1}=-\frac{1}{(k+1{)}^2}{a}_k$。
  • 解出系数：$a_1=-a_0$, $a_2=-\frac{1}{2^2}{a}_1=\frac{1}{2^2}{a}_0$, $a_3=-\frac{1}{3^2}{a}_2=-\frac{1}{3^2\cdot 2^2}{a}_0$, …
  • $a_n=\frac{(-1{)}^n}{(n!{)}^2}{a}_0$。
  • 解为 $y(x)=a_0\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(n!{)}^2}{x}^n$。

  • 收敛半径：用比值判别法，$\lim_{n\to\infty}

    \frac{a_{n+1}x^{n+1}}{a_n x^n}

    = \lim_{n\to\infty}

    \frac{-1}{(n+1)^2} x

    = 0 < 1$\mathrm{对}\mathrm{所}\mathrm{有}$x$\mathrm{成}\mathrm{立}。\mathrm{所}\mathrm{以}$\rho = \infty$。该方程有全局解析解。

• 对于 (E2):
  • $x^2{y}^{″}=\sum _{n=2}^{\mathrm{\infty }}n(n-1)a_n{x}^n$
  • $y^{\prime }=a_1+\sum _{n=2}^{\mathrm{\infty }}n{a}_n{x}^{n-1}$
  • $y=a_0+a_{1}x+\sum _{n=2}^{\mathrm{\infty }}{a}_n{x}^n$
  • 代入 ODE: (Slide 13 的方程是 $a_0+a_1+(a_1+2a_2)x+\sum _{n=2}^{\mathrm{\infty }}[n(n-1)a_n+(n+1)a_{n+1}+a_n]x^n=0$ 吗？检查一下 $y^{\prime }$ 的代入) $y^{\prime }=\sum _{n=1}^{\mathrm{\infty }}n{a}_n{x}^{n-1}$ $y=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n$ $x^2{y}^{″}+y^{\prime }+y=\sum _{n=2}^{\mathrm{\infty }}n(n-1)a_n{x}^n+\sum _{n=1}^{\mathrm{\infty }}n{a}_n{x}^{n-1}+\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n=0$ $\sum _{n=2}^{\mathrm{\infty }}n(n-1)a_n{x}^n+(a_1+2a_{2}x+\sum _{n=3}^{\mathrm{\infty }}n{a}_n{x}^{n-1})+(a_0+a_{1}x+\sum _{n=2}^{\mathrm{\infty }}{a}_n{x}^n)=0$ $\sum _{n=2}^{\mathrm{\infty }}n(n-1)a_n{x}^n+a_1+2a_{2}x+\sum _{k=2}^{\mathrm{\infty }}(k+1)a_{k+1}{x}^k+a_0+a_{1}x+\sum _{n=2}^{\mathrm{\infty }}{a}_n{x}^n=0$ (令 $k=n-1$) $(a_1+a_0)+(2a_2+a_1)x+\sum _{n=2}^{\mathrm{\infty }}[n(n-1)a_n+(n+1)a_{n+1}+a_n]x^n=0$
  • 常数项：$a_1+a_0=0⟹a_1=-a_0$。
  • $x$ 系数：$2a_2+a_1=0⟹a_2=-a_1/2=a_0/2$。
  • $x^n$ 系数 ($n\ge 2$)：$(n(n-1)+1)a_n+(n+1)a_{n+1}=0⟹a_{n+1}=-\frac{n^2-n+1}{n+1}{a}_n$。
  • 递推关系：$a_{n+1}=-\frac{n^2-n+1}{n+1}{a}_n$ for $n\ge 2$。

  • 收敛半径：比值判别法 $\lim_{n\to\infty}

    \frac{a_{n+1}x^{n+1}}{a_n x^n}

    = \lim_{n\to\infty}

    \frac{n^2-n+1}{n+1} x

    = \infty$for$x \neq 0$。

  • 除非 $a_n$ 从某项开始为 0，否则收敛半径 $\rho =0$。
  • 检查 $a_n$ 是否可能为 0：$a_3=-\frac{2^2-2+1}{3}{a}_2=-\frac{3}{3}{a}_2=-a_2=-a_0/2$。 $a_4=-\frac{3^2-3+1}{4}{a}_3=-\frac{7}{4}{a}_3=\frac{7}{8}{a}_0$。系数看起来不会为 0。
  • 结论：对于 (E2)，除了平凡解 $y(x)=0$ (即 $a_0=0$) 之外，不存在以 $x=0$ 为中心的非零解析解。这暗示 $x=0$ 是一个“更坏”的奇点，需要其他方法 (如 Frobenius 方法)。

解析函数的性质 (Properties of Analytic Functions)

定义再述与复/实关系 (Definition Revisited & Complex/Real Relation)

• 解析函数 (Analytic Function): 局部可用收敛幂级数表示 (实解析 vs 复解析/全纯)。
• 中心点 (Center): 幂级数展开的点 $x_0$ 或 $z_0$。通常可以通过平移设为 0。
• 实解析 $⟹$ 复解析 (Slide 15): 一个实轴上的实解析函数，总可以自然地延拓为一个在复平面某个区域内的复解析函数，其幂级数系数相同。因此，研究复解析函数通常更方便，其性质也更强。

收敛半径 (Radius of Convergence)

• 每个幂级数 $\sum a_n(z-z_0{)}^n$ 都存在一个收敛半径 $0\le \rho \le \mathrm{\infty }$。

• 级数在开圆盘 $

  z-z_0

  < \rho$ 内绝对收敛 (Converges Absolutely)。

• 级数在 $

  z-z_0

  \rho$ 外发散 (Diverges)。

• 在边界 $

  z-z_0

  = \rho$ 上行为不定。

• 公式:

  • Hadamard 公式: $\rho = 1 / \limsup_{n\to\infty} \sqrt[n]{

    a_n

    }$ (总适用)

  • 比值判别法: $\rho = \lim_{n\to\infty}

    a_n / a_{n+1}

    $ (仅当极限存在时适用)

核心：利用Hadamard公式计算全纯函数的收敛半径

微分与泰勒级数 (Differentiation and Taylor Series)

• 逐项微分 (Termwise Differentiation): 幂级数可以在其收敛圆盘内部逐项微分任意次，得到的幂级数仍然收敛，且收敛半径不变。 $$f^{\prime }(z)=\sum _{n=1}^{\mathrm{\infty }}n{a}_n(z-z_0{)}^{n-1}$$
• 解析 $⟹C^{\mathrm{\infty }}$: 解析函数必然无穷次可微。
• 泰勒级数 (Taylor Series): 解析函数 $f(z)$ 在 $z_0$ 的幂级数展开就是其泰勒级数： $$f(z)=\sum _{n=0}^{\mathrm{\infty }}\frac{f^{(n)}(z_0)}{n!}(z-z_0{)}^n$$

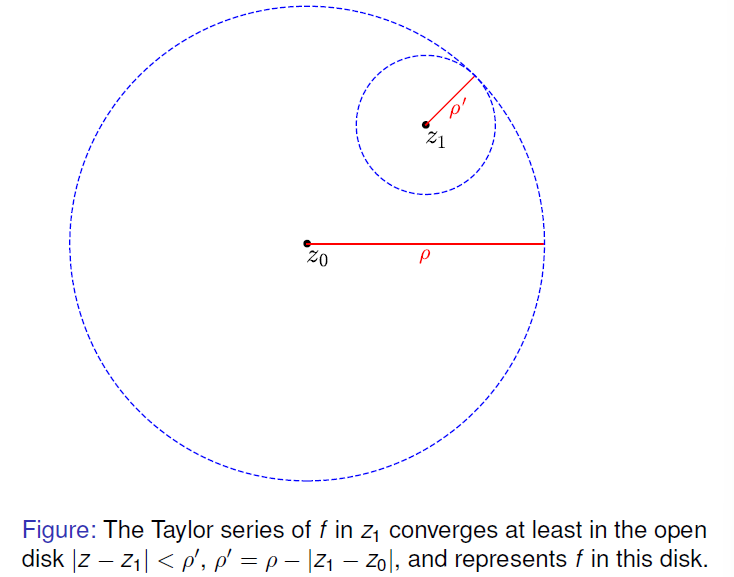
改变中心点 (Expansion with Different Center)

• 核心思想: 一个解析函数可以在其解析域内的任何一点重新展开为幂级数。

• 定理: 如果 $f(z)=\sum a_n(z-z_0{)}^n$ 在 $

  z-z_0

  < \rho$\mathrm{收}\mathrm{敛}，\mathrm{那}\mathrm{么}\mathrm{对}\mathrm{于}\mathrm{任}\mathrm{意}$z_1$\mathrm{满}\mathrm{足}$

  z_1 - z_0

  < \rho$，\mathrm{函}\mathrm{数}$f(z)$\mathrm{可}\mathrm{以}\mathrm{在}$z_1$\mathrm{展}\mathrm{开}\mathrm{为}\mathrm{新}\mathrm{的}\mathrm{幂}\mathrm{级}\mathrm{数}$f(z) = \sum b_k (z-z_1)^k$。

• 新收敛半径: 新级数的收敛半径 ${\rho }^{\prime }$ 至少为 $\rho -

  z_1 - z_0

  $。\mathrm{这}\mathrm{表}\mathrm{示}\mathrm{新}\mathrm{的}\mathrm{收}\mathrm{敛}\mathrm{圆}\mathrm{盘}\mathrm{至}\mathrm{少}\mathrm{能}\mathrm{填}\mathrm{满}\mathrm{以}$z_1$ 为中心、与原收敛圆盘边界相切的区域。

• 证明概要: 利用二项式定理展开 $(z-z_0{)}^n=((z-z_1)+(z_1-z_0){)}^n$，然后重新组合关于 $(z-z_1{)}^k$ 的项。这涉及到双重级数 (Double Series) 的求和顺序交换，其合法性需要级数的绝对收敛 (Absolute Convergence) 来保证。

可视化如下->我们直接考虑在新点展开对应的收敛半径必须满足的要求

双重级数 (Double Series)(Optional)

基本概念与 Fubini 定理 (Basic Concept and Fubini’s Theorem)

• 双重级数 (Double Series): 指的是对一个由两个索引 $m,n$ (通常取非负整数 $\mathbb{N}=0,1,2,\dots$) 标记的项 $a_{mn}$ 进行求和，记为 $\sum _{(m,n)\in \mathbb{N}\times \mathbb{N}}{a}_{mn}$ 或类似形式。可以将其视为一个无限矩阵 (Doubly-Infinite Matrix) $(a_{mn})$ 的所有元素之和。

• Fubini 定理 (用于双重级数): 这是关于双重级数求和顺序交换的一个核心定理。

  • 条件: 定理成立的关键条件是级数的绝对收敛性 (Absolute Convergence)。一个更实用的叙述条件是：存在一个常数 $B>0$，使得对于任意有限的矩形区域 $M,N$，都有 $$\sum _{m=0}^M\sum _{n=0}^N|a_{mn}|\le B$$ (即所有项绝对值的部分和是一致有界的 (Uniformly Bounded))。这个条件实际上就保证了 $\sum _{(m,n)\in \mathbb{N}\times \mathbb{N}}|a_{mn}|$ 是收敛的，即双重级数绝对收敛。
  • 结论: 如果上述条件满足，那么：
    1. 双重级数的总和 $\sum _{(m,n)\in \mathbb{N}\times \mathbb{N}}{a}_{mn}$ 存在。
    2. 可以交换求和顺序: 先按行求和再按列求和，与先按列求和再按行求和的结果相等，并且都等于总和。即： $$\sum _{m=0}^{\mathrm{\infty }}\left(\sum _{n=0}^{\mathrm{\infty }}{a}_{mn}\right)=\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{m=0}^{\mathrm{\infty }}{a}_{mn}\right)=\sum _{(m,n)\in \mathbb{N}\times \mathbb{N}}{a}_{mn}$$ (这里假设了内层的级数也都收敛)。

示例 (Example)

• 考虑 $a_{mn}=\frac{1}{2^m{3}^n}$。
• 按行求和: $r_m=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2^m{3}^n}=\frac{1}{2^m}\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{3}{)}^n=\frac{1}{2^m}\cdot \frac{1}{1-1/3}=\frac{1}{2^m}\cdot \frac{3}{2}$。 再对 $r_m$ 求和: $\sum _{m=0}^{\mathrm{\infty }}{r}_m=\sum _{m=0}^{\mathrm{\infty }}\frac{3}{2}(\frac{1}{2}{)}^m=\frac{3}{2}\cdot \frac{1}{1-1/2}=\frac{3}{2}\cdot 2=3$。
• 按列求和: $c_n=\sum _{m=0}^{\mathrm{\infty }}\frac{1}{2^m{3}^n}=\frac{1}{3^n}\sum _{m=0}^{\mathrm{\infty }}(\frac{1}{2}{)}^m=\frac{1}{3^n}\cdot \frac{1}{1-1/2}=\frac{1}{3^n}\cdot 2$。 再对 $c_n$ 求和: $\sum _{n=0}^{\mathrm{\infty }}{c}_n=\sum _{n=0}^{\mathrm{\infty }}2(\frac{1}{3}{)}^n=2\cdot \frac{1}{1-1/3}=2\cdot \frac{3}{2}=3$。
• 结果验证了 Fubini 定理：两种顺序求和结果相等。
• 类比: 这个例子 $a_{mn}=g(m)h(n)$ 的求和 $\sum a_{mn}=(\sum g(m))(\sum h(n))$ 类似于双重积分 $\iint g(x)h(y)dxdy=(\int g(x)dx)(\int h(y)dy)$。

双重级数和的严格定义 (Rigorous Definition of the Sum)

• “总和 $\sum _{(m,n)}{a}_{mn}$” 到底是什么意思？仅仅定义为 $\underset{M,N\to \mathrm{\infty }}{lim}\sum _{m=0}^M\sum _{n=0}^N{a}_{mn}$ 可能存在问题（例如极限可能依赖于 $M,N$ 趋于无穷的方式，且不一定保证求和顺序可交换）。
• 现代定义 (Modern Definition): 这个定义不依赖于特定的求和顺序（如矩形求和）。 $\sum _{(m,n)\in \mathbb{N}\times \mathbb{N}}{a}_{mn}=A$ 是指： 对于任意给定的误差 $ϵ>0$，都存在一个有限的 (Finite) 索引子集 $F\subset \mathbb{N}\times \mathbb{N}$，使得对于任何包含 $F$ 的有限子集 $E$ ($F\subset E\subset \mathbb{N}\times \mathbb{N}$)，都有 $$|\sum _{(m,n)\in E}{a}_{mn}-A|<ϵ$$
  • 核心: 这个定义基于有限和。只要我们取足够大的有限子集 $F$ 来求和，那么再添加任何其他项（只要总的求和项数仍然有限），其和都非常接近 $A$。
  • 优点: 有限和的求和顺序无关紧要（因为加法满足交换律和结合律），这个定义自然地包含了求和顺序无关性。

现代定义的推论与性质 (Consequences and Properties)

这个现代定义适用于任何（可数）索引集 $I$ 上的求和 $\sum _{i\in I}{a}_i$。对于双重级数，索引集 $I=\mathbb{N}\times \mathbb{N}$。

• 收敛 $⟺$ 绝对收敛: 这是与单变量级数 (如 $\sum _{n=1}^{\mathrm{\infty }}{a}_n$) 最显著的区别之一。对于 $\sum _{i\in I}{a}_i$ 这种形式的和，级数收敛 当且仅当 (if and only if) 它绝对收敛 ($\sum_{i \in I}

  a_i

  $ 收敛)。不存在类似于单变量级数中的“条件收敛”。

  • 技术比喻: 想象在无限大的棋盘上捡硬币。如果你捡起所有硬币的总价值是有限的 (绝对收敛)，那么无论你按什么顺序捡，最终总价值都是一样的。但如果正价值和负价值的硬币分别加起来都是无穷大 (非绝对收敛)，那么你捡硬币的顺序就可能影响你最终得到的总价值（甚至可能得到任何你想要的值，或者根本无法定义一个确定的总和）。现代定义排除了后一种情况。
• 求和顺序无关 (Permutation Invariance): 如果级数收敛（因此绝对收敛），那么任意改变求和顺序（即对索引集 $I$ 进行任意置换 $\pi$），总和不变：$\sum _{i\in I}{a}_i=\sum _{i\in I}{a}_{\pi (i)}$。
• 子集求和: 如果 $\sum _{i\in I}{a}_i$ 存在，那么对于任何子集 $J\subset I$，其和 $\sum _{i\in J}{a}_i$ 也存在。
• 分组求和 (Partitioning Property): 如果级数收敛，你可以将索引集 $I$ 分割成若干不相交的子集 $J_k$ ($I={\cup }_k{J}_k,J_k\cap J_l=\mathrm{\varnothing }$ for $k\ne l$)，然后先对每个子集求和，再将子集的和加起来： $$\sum _{i\in I}{a}_i=\sum _k\left(\sum _{i\in J_k}{a}_i\right)$$

Fubini 定理再解释 (Fubini Explained via Partitioning)

• Fubini 定理本质上是分组求和性质的一个特例。
• 对于双重级数 $\sum _{(m,n)}{a}_{mn}$，索引集 $I=\mathbb{N}\times \mathbb{N}$。
• 按行求和: 是将 $I$ 分割成行 $R_m=(m,n)\mid n\in \mathbb{N}$ (对于 $m=0,1,2,\dots$)。$\sum _m(\sum _{(m,n)\in R_m}{a}_{mn})$。
• 按列求和: 是将 $I$ 分割成列 $C_n=(m,n)\mid m\in \mathbb{N}$ (对于 $n=0,1,2,\dots$)。$\sum _n(\sum _{(m,n)\in C_n}{a}_{mn})$。
• 因为绝对收敛保证了分组求和的合法性，所以按行求和与按列求和的结果相等。

系数比较 / 恒等定理 (Equating Coefficients / Identity Theorem)

• 定理: 如果两个在连通 (Connected) 区域 $D$ 上解析的函数 $f(z)$ 和 $g(z)$，在一个在 $D$ 内有极限点 (Accumulation Point) 的集合 $E$ 上相等 ($f(z)=g(z)$ for $z\in E$)，那么 $f(z)$ 和 $g(z)$ 在整个区域 $D$ 上恒等。
  • 极限点是指该点的任何邻域内都包含 $E$ 中无限多个点。例如，收敛到 $D$ 内部某点的序列 $z_n$ 就是这样一个集合 $E$。
• 推论:
  • 如果一个解析函数在一个区间上为零，则它恒为零。
  • 如果一个解析函数在一列趋于其解析域内某点的点上为零，则它恒为零。
  • 两个解析函数的幂级数在某点 $z_0$ 相同，当且仅当它们在该点的一个邻域内相等。
• 重要性: 这个定理体现了解析函数的“刚性”。它们的值在一个小区域或一个点序列上的表现就决定了它们在整个区域的行为。这就是为什么我们可以通过令幂级数 $\sum c_n(x-x_0{)}^n=0$ 的所有系数 $c_n=0$ 来解微分方程。
• 对比 $C^{\mathrm{\infty }}$ (Slide 29): 实 $C^{\mathrm{\infty }}$ 函数没有这种刚性。$f(x)=e^{-1/x^2}$ ($f(0)=0$) 在 $x\le 0$ 上恒等于 0 函数，但在 $x>0$ 却不为 0。

代数运算 (Algebraic Operations)

• 加减、数乘: 逐项进行，收敛半径 $\rho \ge min({\rho }_f,{\rho }_g)$。
• 乘法 (Cauchy Product): $$f(z)g(z)=(\sum a_n{z}^n)(\sum b_k{z}^k)=\sum _{n=0}^{\mathrm{\infty }}(\sum _{k=0}^n{a}_k{b}_{n-k})z^n$$ 收敛半径 $\rho \ge min({\rho }_f,{\rho }_g)$。
• 除法: 如果 $g(z_0)\ne 0$，则 $h(z)=f(z)/g(z)$ 在 $z_0$ 附近解析。其系数 $c_n$ 可以通过解方程 $\sum a_n{z}^n=(\sum b_k{z}^k)(\sum c_j{z}^j)$ 逐项确定：
  • $a_0=b_0{c}_0⟹c_0=a_0/b_0$
  • $a_1=b_0{c}_1+b_1{c}_0⟹c_1=(a_1-b_1{c}_0)/b_0$
  • 以此类推。
• 复合 (Composition): 若 $f$ 在 $z_0$ 解析, $g$ 在 $w_0=f(z_0)$ 解析, 则 $g(f(z))$ 在 $z_0$ 解析。计算其系数比较复杂，需要展开嵌套幂级数。
• 应用：生成函数 (Generating Functions, Slides 35-41):
  • 这些例子 (Fibonacci, Euler, Bernoulli 数) 展示了代数运算的威力。通过函数的代数关系（如 $f(z)=1/(1-z-z^2)$）和幂级数运算，可以推导出数列系数的递推关系或性质。例如，从 $1=(1-z-z^2)\sum f_n{z}^n$ 得到斐波那契数列的递推关系 $f_n=f_{n-1}+f_{n-2}$。

零点和极点 (Zeros and Poles)

• 零点 (Zero): 如果解析函数 $f(z)$ 在 $z_0$ 不恒为零，但 $f(z_0)=0$，则存在唯一的整数 $m\ge 1$ (零点的阶 (Order)) 使得 $f(z)=(z-z_0{)}^{m}h(z)$，其中 $h(z)$ 在 $z_0$ 解析且 $h(z_0)\ne 0$。

• 极点 (Pole): 如果 $h(z)$ 在 $z_0$ 的去心邻域 $0 <

  z-z_0

  < \delta$\mathrm{解}\mathrm{析}，\mathrm{但}$\lim_{z\to z_0}

  h(z)

  = \infty$，\mathrm{则}$z_0$\mathrm{是}$h(z)$\mathrm{的}\mathrm{极}\mathrm{点}。\mathrm{存}\mathrm{在}\mathrm{唯}\mathrm{一}\mathrm{的}\mathrm{整}\mathrm{数}$m \ge 1$ (极点的阶 (Order)) 使得 $h(z)=(z-z_0{)}^{-m}g(z)$，其中 $g(z)$ 在 $z_0$ 解析且 $g(z_0)\ne 0$。

• 函数商 $h=f/g$ (Slide 42): 若 $f$ 在 $z_0$ 有 $m_1$ 阶零点，$g$ 有 $m_2$ 阶零点，则 $h$ 在 $z_0$ 的行为由 $m=m_1-m_2$ 决定：
  • $m>0$: $h$ 有 $m$ 阶零点。
  • $m=0$: $h$ 在 $z_0$ 解析且非零 ($h(z_0)\ne 0$)。

  • $m<0$: $h$ 有 $

    m

    $ 阶极点。

高级性质 (复分析结果) (Advanced Properties)

• 可微 $⟺$ 解析: 在复数域，一阶可微（满足柯西-黎曼方程 Cauchy-Riemann equations）就保证了无穷次可微和解析性。
• 收敛半径与奇点:
  • 定理: 全纯 (解析) 函数 $f(z)$ 在 $z_0$ 的泰勒级数 $\sum a_n(z-z_0{)}^n$ 的收敛半径 $\rho$ 等于 $z_0$ 到 $f(z)$ 最近的奇点 (Singularity) 的距离。奇点是函数失去解析性的点 (通常是无定义点或出现极点、本质奇点等)。
  • 意义: 函数能否在某点展开为收敛幂级数，以及收敛范围多大，完全取决于其在复平面上的奇点分布。

  • 示例 (几何级数 $1/(1-z)$, Slide 47-49): 奇点在 $z=1$。在 $z_0=0$ 展开，$\rho=

    1-0

    =1$。\mathrm{在}$z_0=a$($a \neq 1$)\mathrm{展}\mathrm{开}，$\rho=

    1-a

    $。

  • 示例 ($1/(1+z^2)$, Slide 50-51): 奇点在 $z=\pm i$。在 $z_0=0$ 展开，$\rho=

    \pm i - 0

    =1$。\mathrm{在}$z_0=1$\mathrm{展}\mathrm{开}，$\rho=

    \pm i - 1

    = \sqrt{1^2+(\pm 1)^2} = \sqrt{2}$。\mathrm{在}$z_0=1+i$\mathrm{展}\mathrm{开}，\mathrm{最}\mathrm{近}\mathrm{奇}\mathrm{点}\mathrm{是}$i$，\mathrm{距}\mathrm{离}$

    i - (1+i)

    =

    -1

    = 1$，\mathrm{所}\mathrm{以}$\rho=1$。

  • 解释实函数现象: 这解释了为什么实函数 $1/(1+x^2)$ 的泰勒级数只在 $(-1,1)$ 收敛，即使它在 $\mathbb{R}$ 上处处光滑——因为复平面上的奇点 $z=\pm i$ 限制了收敛半径为 1。

二阶线性 ODE 的级数解 (Series Solutions of 2nd-Order Linear ODE’s)

现在我们将前面关于幂级数和解析函数的知识应用于求解二阶线性 ODE $P(x)y^{″}+Q(x)y^{\prime }+R(x)y=0$ (或非齐次的 $P(x)y^{″}+Q(x)y^{\prime }+R(x)y=S(x)$)，其中 $P,Q,R,S$ 是解析函数。

常点和奇点 (Ordinary and Singular Points)

• 定义:
  • 如果 $P(x_0)\ne 0$，则 $x_0$ 是 ODE 的常点 (Ordinary Point)。
  • 如果 $P(x_0)=0$，则 $x_0$ 是 ODE 的奇点 (Singular Point)。
• 在常点 $x_0$ 附近:
  • ODE 可以写成 $y^{″}+p(x)y^{\prime }+q(x)y=0$，其中 $p(x)=Q(x)/P(x)$ 和 $q(x)=R(x)/P(x)$ 在 $x_0$ 附近是解析的。
• 在奇点 $x_0$ 附近:
  • 我们需要区分奇点的类型。
  • 正则奇点 (Regular Singular Point): 如果 $x_0$ 是奇点，并且极限 $$p_0=\underset{x\to x_0}{lim}(x-x_0)p(x)=\underset{x\to x_0}{lim}(x-x_0)\frac{Q(x)}{P(x)}$$ $$q_0=\underset{x\to x_0}{lim}(x-x_0{)}^{2}q(x)=\underset{x\to x_0}{lim}(x-x_0{)}^2\frac{R(x)}{P(x)}$$ 都存在且有限。这等价于说 $(x-x_0)p(x)$ 和 $(x-x_0{)}^{2}q(x)$ 在 $x_0$ 处是解析的 (可以通过定义它们在 $x_0$ 的值为上述极限值)。
  • 非正则奇点 (Irregular Singular Point): 不是正则奇点的奇点。
  • 等价形式 (设 $x_0=0$): ODE 可以写成 $x^2{y}^{″}+x(xp(x))y^{\prime }+(x^{2}q(x))y=0$，其中 $f(x)=xp(x)=\sum _{n=0}^{\mathrm{\infty }}{p}_n{x}^n$ 和 $g(x)=x^{2}q(x)=\sum _{n=0}^{\mathrm{\infty }}{q}_n{x}^n$ 在 $x=0$ 附近是解析的。$p_0,q_0$ 就是上面定义的极限值。
• 指标方程 (Indicial Equation): 与正则奇点 $x_0$ (设 $x_0=0$) 相关联的二次方程是： $$F(r)=r(r-1)+p_{0}r+q_0=0$$ 它的根 $r_1,r_2$ 称为 ODE 在奇点 $x_0$ 处的指标 (Exponents)。这个方程来源于尝试用 $y=x^r$ 求解相关的欧拉方程 (Euler Equation) $x^2{y}^{″}+p_{0}x{y}^{\prime }+q_{0}y=0$ (这是原 ODE 通过截断 $xp(x)$ 和 $x^{2}q(x)$ 的级数得到的近似)。

Frobenius Method 递推关系求解

为简化起见，我们假设奇点在 $x_0=0$。微分方程的形式为： $$x^2{y}^{″}+x(xp(x))y^{\prime }+(x^{2}q(x))y=0$$ 其中：

• $xp(x)=f(x)=\sum _{k=0}^{\mathrm{\infty }}{p}_k{x}^k=p_0+p_{1}x+p_2{x}^2+\dots$
• $x^{2}q(x)=g(x)=\sum _{k=0}^{\mathrm{\infty }}{q}_k{x}^k=q_0+q_{1}x+q_2{x}^2+\dots$
• 我们对解的 Frobenius 拟设 (Ansatz) 是 $y(x)=\sum _{j=0}^{\mathrm{\infty }}{a}_j{x}^{j+r}$ (这里我用 $j$ 作为 $y$ 的求和下标，以避免与后面的 $N$ 混淆)。

解的导数是：

• $y^{\prime }(x)=\sum _{j=0}^{\mathrm{\infty }}(j+r)a_j{x}^{j+r-1}$
• $y^{\prime }‘(x)=\sum _{j=0}^{\mathrm{\infty }}(j+r)(j+r-1)a_j{x}^{j+r-2}$

现在，我们将这些代入微分方程的各个部分：

1. 第一项: $x^2{y}^{″}$ $$x^2{y}^{″}=x^2\sum _{j=0}^{\mathrm{\infty }}(j+r)(j+r-1)a_j{x}^{j+r-2}=\sum _{j=0}^{\mathrm{\infty }}(j+r)(j+r-1)a_j{x}^{j+r}$$

2. 第二项: $x(xp(x))y^{\prime }=xf(x)y^{\prime }$ $$xf(x)y^{\prime }=x\left(\sum _{k=0}^{\mathrm{\infty }}{p}_k{x}^k\right)(\sum _{j=0}^{\mathrm{\infty }}(j+r)a_j{x}^{j+r-1})$$ 首先，我们计算乘积 $f(x)y^{\prime }$。这是两个幂级数的柯西乘积 (Cauchy product)。 这个乘积中一般项的 $x$ 的幂次是 $x^k\cdot x^{j+r-1}=x^{k+j+r-1}$。 所以，$f(x)y^{\prime }=\sum _{m=0}^{\mathrm{\infty }}(\sum _{k=0}^m{p}_k\cdot ((m-k)+r)a_{m-k})x^{m+r-1}$。 (这里，$m=k+j$，所以 $j=m-k$。来自 $y^{\prime }$ 的系数是 $(j+r)a_j=((m-k)+r)a_{m-k}$。) 然后，再乘以 $x$： $$xf(x)y^{\prime }=\sum _{m=0}^{\mathrm{\infty }}(\sum _{k=0}^m{p}_k(m-k+r)a_{m-k})x^{m+r}$$

3. 第三项: $(x^{2}q(x))y=g(x)y$ $$g(x)y=\left(\sum _{k=0}^{\mathrm{\infty }}{q}_k{x}^k\right)\left(\sum _{j=0}^{\mathrm{\infty }}{a}_j{x}^{j+r}\right)$$ 这是另一个柯西乘积。一般项的 $x$ 的幂次是 $x^k\cdot x^{j+r}=x^{k+j+r}$。 $$g(x)y=\sum _{m=0}^{\mathrm{\infty }}\left(\sum _{k=0}^m{q}_k{a}_{m-k}\right)x^{m+r}$$ (这里，$m=k+j$，所以 $j=m-k$。来自 $y$ 的系数是 $a_j=a_{m-k}$。)

合并各项并令系数为零

微分方程指出这三项之和为零： $$\sum _{j=0}^{\mathrm{\infty }}(j+r)(j+r-1)a_j{x}^{j+r}+\sum _{m=0}^{\mathrm{\infty }}(\sum _{k=0}^m{p}_k(m-k+r)a_{m-k})x^{m+r}+\sum _{m=0}^{\mathrm{\infty }}\left(\sum _{k=0}^m{q}_k{a}_{m-k}\right)x^{m+r}=0$$ 为了使这个等式对收敛区间内的所有 $x$ 都成立， $x$ 的每一项幂次的系数都必须为零。我们来看 $x^{N+r}$ (对于某个整数 $N\ge 0$) 的系数。为此，我们在第一个和中令 $j=N$，在第二个和第三个和中令 $m=N$。

$x^{N+r}$ 的系数是： $$(N+r)(N+r-1)a_N+(\sum _{k=0}^N{p}_k(N-k+r)a_{N-k})+\left(\sum _{k=0}^N{q}_k{a}_{N-k}\right)=0$$ 现在，我们想把包含 $a_N$ 的项分离出来，并将其余的项 (它们将包含 $a_0,a_1,\dots ,a_{N-1}$) 组合在一起。

我们展开这些和式： 在 $\sum _{k=0}^N{p}_k(N-k+r)a_{N-k}$ 中，包含 $a_N$ 的项发生在 $k=0$ 时： $p_0(N-0+r)a_{N-0}=p_0(N+r)a_N$。 在 $\sum _{k=0}^N{q}_k{a}_{N-k}$ 中，包含 $a_N$ 的项发生在 $k=0$ 时： $q_0{a}_{N-0}=q_0{a}_N$。

所以，我们可以把所有包含 $a_N$ 的项提出来： $$[(N+r)(N+r-1)+p_0(N+r)+q_0]a_N$$ 方括号中的表达式正是 $F(N+r)$，其中 $F(s)=s(s-1)+p_{0}s+q_0$ 是指标多项式。 因此，包含 $a_N$ 的项合起来就是 $F(N+r)a_N$。

和式中剩下的项包含 $a_{N-k}$，其中 $k$ 从 $1$ 到 $N$。

• 对于包含 $p_k$ 的和式，剩下的部分是：$\sum _{k=1}^N{p}_k(N-k+r)a_{N-k}$。 令 $j^{\prime }=N-k$。当 $k$ 从 $1$ 变到 $N$ 时，$j^{\prime }$ 从 $N-1$ 变到 $0$。 所以，这部分可以写成 $\sum _{j^{\prime }=0}^{N-1}{p}_{N-j^{\prime }}(j^{\prime }+r)a_{j^{\prime }}$。

• 对于包含 $q_k$ 的和式，剩下的部分是：$\sum _{k=1}^N{q}_k{a}_{N-k}$。 同样令 $j^{\prime }=N-k$，这部分可以写成 $\sum _{j^{\prime }=0}^{N-1}{q}_{N-j^{\prime }}{a}_{j^{\prime }}$。

将这些合并起来，$x^{N+r}$ 的系数方程变为： $$F(N+r)a_N+\sum _{j^{\prime }=0}^{N-1}{p}_{N-j^{\prime }}(j^{\prime }+r)a_{j^{\prime }}+\sum _{j^{\prime }=0}^{N-1}{q}_{N-j^{\prime }}{a}_{j^{\prime }}=0$$ 我们可以合并后两个和式： $$F(N+r)a_N+\sum _{j^{\prime }=0}^{N-1}[p_{N-j^{\prime }}(j^{\prime }+r)+q_{N-j^{\prime }}]a_{j^{\prime }}=0$$ 最后，解出 $F(N+r)a_N$： $$F(N+r)a_N=-\sum _{j^{\prime }=0}^{N-1}[(j^{\prime }+r)p_{N-j^{\prime }}+q_{N-j^{\prime }}]a_{j^{\prime }}$$ 这就是递推关系。如果我们将求和下标 $j^{\prime }$ 替换回更常用的 $k$，就得到： $$F(N+r)a_N=-\sum _{k=0}^{N-1}[(k+r)p_{N-k}+q_{N-k}]a_k$$ 这个公式对 $N\ge 1$ 成立。

检验 $N=0$ 的情况 (指标方程): 当 $N=0$ 时，和式 $\sum _{k=0}^{-1}$ 是一个空和，定义为 0。 所以，对于 $N=0$，方程是 $F(0+r)a_0=0⟹F(r)a_0=0$。 由于我们假设 $a_0\ne 0$ (否则我们会得到一个平凡解，或者解实际上对应于一个更高次幂的 $r$)，这迫使 $F(r)=0$，这确实就是指标方程。

所以，对于 $n\ge 1$，完整的递推关系是： $$F(r+n)a_n=-\sum _{k=0}^{n-1}[(k+r)p_{n-k}+q_{n-k}]a_k$$ 这个关系式允许我们在已知 $a_0,a_1,\dots ,a_{n-1}$ 的情况下计算出 $a_n$，前提是 $F(r+n)\ne 0$。而 $r$ 的值是从指标方程 $F(r)=0$ 的根中选取的。

• $(k+r)p_{n-k}$ 这一项来自于 $xf(x)y^{\prime }$：$a_k$ 对应 $x^{k+r}$ 因子，$(k+r)$ 是它在求导时的“有效”幂次 (与 $a_k$ 相关联的项 $a_k{x}^{k+r}$ 经过 $y^{\prime }$ 运算后得到 $(k+r)a_k{x}^{k+r-1}$，再与 $f(x)$ 中的 $p_{n-k}{x}^{n-k}$ 和外面的 $x$ 乘起来贡献到 $x^{n+r}$ 项)。
• $q_{n-k}$ 这一项来自于 $g(x)y$：$a_k$ 对应 $x^{k+r}$，与 $g(x)$ 中的 $q_{n-k}{x}^{n-k}$ 乘起来贡献到 $x^{n+r}$ 项。
• 和式 $\sum _{k=0}^{n-1}$ 确保我们收集了所有由低阶的 $a_k$ 与适当的 $p_j$ 和 $q_j$ 相乘而对 $x^{n+r}$ 项产生的贡献。

初值选择 一般我们设定 $a_0=1$ （或者其他任意非0常数，但是1是标准做法）

解析情况：常点附近的解 (The Analytic Case: Solutions near an Ordinary Point)

(对应 Slides 57-75)

• 定理 : 如果 $x_0$ 是 $P(x)y^{″}+Q(x)y^{\prime }+R(x)y=0$ 的一个常点，并且 $p(x)=Q/P,q(x)=R/P$ 的幂级数在 $

  x-x_0

  < \rho$ 收敛，那么对于任意初始条件 $y(x_0)=a_0,y^{\prime }(x_0)=a_1$，存在唯一的解析解 $y(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n(x-x_0{)}^n$，且该级数至少在 $

  x-x_0

  < \rho$ 内收敛。

tip 收敛半径 $\rho$ 可由级数 $p(x),q(x)$ 在 $x_0$ 处的各自收敛半径的最小值确定

• 求解方法:
  1. 设 $y(x)=\sum _{n=0}^{\mathrm{\infty }}{a}_n(x-x_0{)}^n$。
  2. 将 $y,y^{\prime },y^{″}$ 的级数代入 ODE (通常使用 $y^{\prime }‘+p(x)y^{\prime }+q(x)y=0$ 的形式，并将 $p(x),q(x)$ 也展开为关于 $(x-x_0)$ 的幂级数)。
  3. 合并所有项，得到一个关于 $(x-x_0)$ 的幂级数等于 0。
  4. 根据解析函数的唯一性 (性质 5)，幂级数恒为 0 当且仅当所有系数为 0。令 $(x-x_0{)}^n$ 的系数为 0，得到关于 $a_n$ 的递推关系 (Recurrence Relation)。
  5. 利用初始条件 $a_0=y(x_0),a_1=y^{\prime }(x_0)$，通过递推关系计算出所有 $a_n$ ($n\ge 2$)。
• 示例 (Airy 方程 $y^{″}-xy=0$ ): $x_0=0$ 是常点。$p(x)=0,q(x)=-x$ 都是解析的，$\rho =\mathrm{\infty }$。
  • Ansatz: $y=\sum a_n{x}^n$. $y^{″}=\sum (n+2)(n+1)a_{n+2}{x}^n$. $xy=\sum a_n{x}^{n+1}=\sum a_{n-1}{x}^n$ ($n\ge 1$)。
  • ODE: $\sum _{n=0}^{\mathrm{\infty }}(n+2)(n+1)a_{n+2}{x}^n-\sum _{n=1}^{\mathrm{\infty }}{a}_{n-1}{x}^n=0$。
  • $n=0$: $2\cdot 1a_2=0⟹a_2=0$。
  • $n\ge 1$: $(n+2)(n+1)a_{n+2}-a_{n-1}=0⟹a_{n+2}=\frac{a_{n-1}}{(n+2)(n+1)}$。
  • $a_0,a_1$ 任意。
  • $a_3=a_0/(3\cdot 2)$。 $a_4=a_1/(4\cdot 3)$。 $a_5=a_2/(5\cdot 4)=0$。 $a_6=a_3/(6\cdot 5)=a_0/((6\cdot 5)(3\cdot 2))$。 $a_7=a_4/(7\cdot 6)=a_1/((7\cdot 6)(4\cdot 3))$。 $a_8=a_5/(\dots )=0$。
  • 解的形式为 $y(x)=a_0{y}_1(x)+a_1{y}_2(x)$，其中 $y_1$ 只含 $x^{3k}$ 次项，$y_2$ 只含 $x^{3k+1}$ 次项。收敛半径 $\rho =\mathrm{\infty }$。

• 示例 (Legendre 方程 $(1-x^2)y^{″}-2x{y}^{\prime }+n(n+1)y=0$): $x_0=0$ 是常点。$p(x)=-2x/(1-x^2),q(x)=n(n+1)/(1-x^2)$ 在 $

  x

  <1$\mathrm{解}\mathrm{析}，$\rho=1$。

  • 直接用原方程代入 $y=\sum a_k{x}^k$。
  • 得到递推关系 $a_{k+2}=\frac{k(k+1)-n(n+1)}{(k+2)(k+1)}{a}_k=-\frac{(n-k)(n+k+1)}{(k+2)(k+1)}{a}_k$。
  • 得到两个线性无关解 $y_1$ (偶函数) 和 $y_2$ (奇函数)。
  • 当 $n$ 为整数时，其中一个级数会终止，成为 $n$ 次多项式，即勒让德多项式 (Legendre Polynomial) $P_n(x)$ (乘以一个归一化因子)。另一个解则不是多项式，收敛半径为 1。
• 非齐次方程 (Inhomogeneous Equations): 如果 $x_0$ 是常点且非齐次项 $S(x)$ 在 $x_0$ 解析，那么 $P{y}^{″}+Q{y}^{\prime }+Ry=S$ 的特解 $y_p(x)$ 也在 $x_0$ 解析。其收敛半径至少是 $p(x),q(x),r(x)=S(x)/P(x)$ 中最小的收敛半径。证明可用参数变易法 (Variation of Parameters)。

• 示例 ($y^{\prime }‘+y=1/(1-x)$): $x_0=0$ 是常点。$p=0,q=1$。$r(x)=1/(1-x)=\sum x^n$ 在 $

  x

  <1$\mathrm{收}\mathrm{敛}，$\rho=1$。

  • Ansatz: $y=\sum a_n{x}^n$。$y(0)=a_0=0,y^{\prime }(0)=a_1=0$。
  • ODE: $\sum (n+2)(n+1)a_{n+2}{x}^n+\sum a_n{x}^n=\sum x^n$。
  • 比较系数：$(n+2)(n+1)a_{n+2}+a_n=1$ for $n\ge 0$。
  • $a_2=(1-a_0)/(2\cdot 1)=1/2$。 $a_3=(1-a_1)/(3\cdot 2)=1/6$。 $a_4=(1-a_2)/(4\cdot 3)=(1-1/2)/12=1/24$。 $a_5=(1-a_3)/(5\cdot 4)=(1-1/6)/20=(5/6)/20=5/120=1/24$。
  • 级数解为 $y(x)=\frac{1}{2}{x}^2+\frac{1}{6}{x}^3+\frac{1}{24}{x}^4+\frac{1}{24}{x}^5+\dots$。收敛半径 $\rho =1$。

正则奇点情况：Frobenius 方法 (The Case of a Regular Singular Point: The Method of Frobenius)

当 $x_0$ 是正则奇点时，解通常不再是标准的幂级数，可能包含对数项或形如 $(x-x_0{)}^r$ 的因子，其中 $r$ 不是整数。

• Frobenius Ansatz (设 $x_0=0$): 尝试寻找形如 $$y(x)=x^r\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^n=\sum _{n=0}^{\mathrm{\infty }}{a}_n{x}^{n+r}(a_0\ne 0)$$ 的解。这里的 $r$ 是待定常数 (可能是复数)，$a_n$ 是系数。
• 求解过程:
  1. 计算 $y^{\prime },y^{″}$ 的级数形式。
  2. 代入 ODE 的形式 $x^2{y}^{″}+x(xp(x))y^{\prime }+(x^{2}q(x))y=0$，其中 $xp(x)=\sum p_n{x}^n,x^{2}q(x)=\sum q_n{x}^n$。
  3. 合并同类项 $x^{n+r}$。
  4. 令最低次项 ($n=0$，即 $x^r$) 的系数为 0，得到指标方程 $F(r)=r(r-1)+p_{0}r+q_0=0$。指标 $r$ 必须是这个方程的根 $r_1,r_2$。
  5. 令 $x^{n+r}$ ($n\ge 1$) 的系数为 0，得到关于 $a_n$ 的递推关系，形式通常为 $F(r+n)a_n=-\sum _{k=0}^{n-1}[\dots ]a_k$ 。
• Frobenius 定理: 描述解的形式，取决于指标 $r_1,r_2$ 的关系 (设 $\text{Re}(r_1)\ge \text{Re}(r_2)$)：
  • 情况 1: $r_1-r_2$ 不是整数。 存在两个线性无关的解： $y_1(x)=|x{|}^{r_1}\sum _{n=0}^{\mathrm{\infty }}{a}_n(r_1)x^n(a_0=1)$ $y_2(x)=|x{|}^{r_2}\sum _{n=0}^{\mathrm{\infty }}{a}_n(r_2)x^n(a_0=1)$ (系数 $a_n(r_i)$ 由代入 $r=r_i$ 的递推关系确定)。注意使用 $|x{|}^r$ 形式可以包含 $x<0$ 的情况 (Slide 83)。
  • 情况 2: $r_1=r_2=r$ (重根)。 第一个解形式同上： $y_1(x)=|x{|}^r\sum _{n=0}^{\mathrm{\infty }}{a}_n(r)x^n(a_0=1)$ 第二个解包含对数项： $y_2(x)=y_1(x)\ln |x|+|x{|}^r\sum _{n=1}^{\mathrm{\infty }}{b}_n{x}^n$ 其中 $b_n=\frac{d{a}_n(r)}{dr}{|}_{r=r_1}$。
  • 情况 3: $r_1-r_2=N$ 是一个正整数。 第一个解对应较大的根 $r_1$： $y_1(x)=|x{|}^{r_1}\sum _{n=0}^{\mathrm{\infty }}{a}_n(r_1)x^n(a_0=1)$ 第二个解可能包含对数项： $y_2(x)=a{y}_1(x)\ln |x|+|x{|}^{r_2}\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n(c_0=1)$ 其中常数 $a=\underset{r\to r_2}{lim}(r-r_2)a_N(r)$ (可能为 0)，系数 $c_n=\frac{d}{dr}[(r-r_2)a_n(r)]{|}_{r=r_2}$ for $n\ge 1$。如果 $a=0$，则第二个解不含对数项，形式与情况 1 类似。
• 求解技巧 (Slide 84): 计算 $a_n^{\prime }(r)$ 或 $c_n$ 可能很复杂。实践中，常常先求出 $y_1(x)$，然后将 $y_2(x)$ 的形式 (包含待定系数 $b_n$ 或 $c_n$ 和常数 $a$) 代入 ODE，直接求解这些系数。
• 示例 1 ($2x{y}^{″}+y^{\prime }+xy=0$, Slide 92-97): $x_0=0$ 是正则奇点。$p_0=1/2,q_0=0$。指标方程 $r(r-1/2)=0⟹r_1=1/2,r_2=0$。$r_1-r_2=1/2$ 不是整数，属于情况 1。
  • $r_1=1/2$: Ansatz $y=\sum a_n{x}^{n+1/2}$。代入 ODE，得到 $a_1=0$ 且 $a_n=-a_{n-2}/(n(2n+1))$ for $n\ge 2$。得到 $y_1(x)$，只含奇数次根式项 $x^{2k+1/2}$。
  • $r_2=0$: Ansatz $y=\sum a_n{x}^n$。代入 ODE，得到 $a_1=0$ 且 $a_n=-a_{n-2}/(n(2n-1))$ for $n\ge 2$。得到 $y_2(x)$，只含偶数次幂 $x^{2k}$。
  • 两个解都是无穷级数，收敛半径 $\rho =\mathrm{\infty }$。
• 示例 2 (Legendre 方程 near $x=1$, Slide 98-109): $x_0=1$ 是正则奇点。$p_0=1,q_0=0$。指标方程 $r^2=0⟹r_1=r_2=0$。属于情况 2 (重根)。
  • $r_1=0$: 第一个解 Ansatz $y=\sum a_k(x-1{)}^k$ (因为 $r=0$)。代入变换后的 ODE (以 $t=x-1$ 为变量)，得到 $a_{k+1}=\frac{(n-k)(n+k+1)}{2(k+1{)}^2}{a}_k$。发现当 $a_0$ 取特定值时，解就是 $P_n(x)$。所以 $y_1(x)=P_n(x)$。

  • 第二个解形式为 $y_2(x) = P_n(x) \ln

    x-1

    \sum_{k=1}^{\infty} b_k (x-1)^k$。\mathrm{将}\mathrm{此}\mathrm{形}\mathrm{式}\mathrm{代}\mathrm{入}ODE\mathrm{可}\mathrm{以}\mathrm{解}\mathrm{出}$b_k$。

  • 对于 $n=0$ ($P_0=1$) 和 $n=1$ ($P_1=x=t+1$)，分别求出了 $b_k$ 的级数，并与已知的第二类勒让德函数 (Legendre Q-function) $Q_n(x)$ 联系起来。例如，对于 $n=0$，$y_2(x) = \ln(x-1) - \sum_{k=1}^\infty \frac{(-1)^k}{k 2^k} (x-1)^k \propto \ln

    \frac{x-1}{x+1}

    \propto Q_0(x)$。