First-Order Differential Equations2

#Math285

Separable Differential Equations

可分离微分方程

1. 形式
Separable Differential Equations（一阶）为一阶微分方程中的一个子类，形如：

$$\begin{array}{rlrl}& M(x)+N(y)\frac{dy}{dx}=0& \text{or}& M(x)dx+N(y)dy=0\end{array}$$

2. 求解
核心即为将自变量与因变量对应的函数分别分离，然后直接积分即可

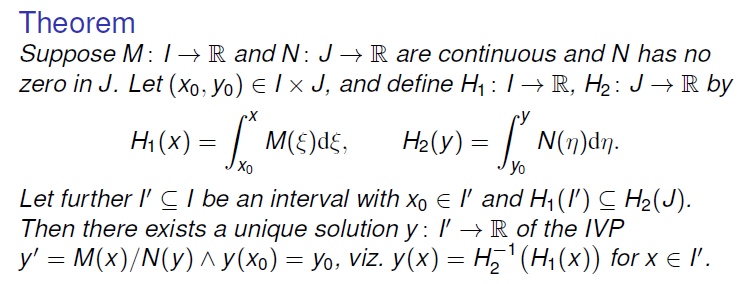
3. 核心思想
对于可分离形式的微分方程，其可以写为:

$$\begin{array}{rlr}& y^{\prime }=\frac{dy}{dx}=\frac{M(x)}{N(y)}& M(x)dx-N(y)dy=0\end{array}$$

然后直接两边同时积分，同时结合初值即可得到唯一解（注意积分起点为初值）（一般来说先得到的为 implicit form 形式，可根据化简的难易程度决定是否化为 explicit form）

[!warning] 注意
求解定义域的过程不要只关注原始方程以及最终方程

• 关注原始方程对于 y 的要求反推对于 x 的要求
• 中间每个过程都要注意满足初始要求

Example

---

注意整体定义域被 0 分成了两段，需要根据初始值确定唯一解

---

General Remarks

[!tip] Summary

• $f_2$ 的零点（如果有）将 $J$ 划分成开子区间，在每个子区间上，初值问题都有局部解的存在性和唯一性
• 对于任何满足 $f_2(y_0)=0$ 的点 $y_0$ ​，有常值解 $y(x)=y_0$
• 每个一阶可分离微分方程均有解，但在整个定义域上解的唯一性需要额外假设
  ​

线性一阶微分方程与一阶可分离方程的区别

Logistic Equation

形式

$$y^{\prime }=ay-b{y}^2$$

其中 $a,b>0$
该方程用来作为描述人口增长的数学模型

解

1. 稳态解 ->即右式的零点

$$\begin{array}{rlr}& y\equiv 0& y\equiv \frac{a}{b}\end{array}$$

2. 一般解

渐近线的性质

1. 参数 $d$ 的意义

参数 $d$ 与初值 $y_0=y(0)$ 的关系为：

$$d=\frac{a}{y_0}-b$$

因此，$y_0$ 的不同取值决定了解的不同行为：

• 当 $y_0=0$ 时，$d=\mathrm{\infty }$，对应稳态解 $y\equiv 0$
• 当 $y_0=a/b$ 时，$d=0$，对应稳态解 $y\equiv a/b$
• 当 $0<y_0<a/b$ 时，$d>0$
• 当 $y_0>a/b$ 时，$d<0$ 且 $d>-b$
• 当 $y_0<0$ 时，$d<-b$

2. 渐近线行为详细分析

情况 1: $d>0$ (对应 $0<y_0<a/b$)

• 定义域：$t\in \mathbb{R}$（即解在整个实数轴上有定义）
• 单调性：解 $y(t)$ 严格单调递增
• 水平渐近线：
  • $\underset{t\to +\mathrm{\infty }}{lim}y(t)=\frac{a}{b}$
  • $\underset{t\to -\mathrm{\infty }}{lim}y(t)=0$
• 拐点：解曲线有一个拐点，出现在 $t=t_h$，其中 $t_h=(\ln d-\ln b)/a$
• 凸凹性：
  • 在 $[-\mathrm{\infty },t_h]$ 上函数是凸的（因为 $0<y(t)<a/2b$）
  • 在 $[t_h,+\mathrm{\infty }]$ 上函数是凹的

这种情况下的曲线呈现典型的 S 形（sigmoid 形状），被称为 logistic 增长曲线。

---

情况 2: $d<0$ 且 $-b<d<0$ (对应 $y_0>a/b$)

• 垂直渐近线：$t_{\mathrm{\infty }}=(\ln (-d)-\ln b)/a<0$
• 定义域：$(t_{\mathrm{\infty }},+\mathrm{\infty })$
• 单调性：解 $y(t)$ 严格单调递减
• 曲线行为：
  • $\underset{t\downarrow t_{\mathrm{\infty }}}{lim}y(t)=+\mathrm{\infty }$
  • $\underset{t\to +\mathrm{\infty }}{lim}y(t)=\frac{a}{b}$
• 凸凹性：在整个定义域内保持凸性

---

情况 3: $d<-b$ (对应 $y_0<0$)

• 垂直渐近线：$t_{\mathrm{\infty }}=(\ln (-d)-\ln b)/a>0$
• 定义域：$(-\mathrm{\infty },t_{\mathrm{\infty }})$
• 曲线行为：
  • $\underset{t\to -\mathrm{\infty }}{lim}y(t)=0$
  • $\underset{t\uparrow t_{\mathrm{\infty }}}{lim}y(t)=-\mathrm{\infty }$

---

情况 4: $d=-b$ (特殊情况)

这种情况下，解有两个分支，它们在 $t_{\mathrm{\infty }}=0$ 处有垂直渐近线。

3. 最大解的分类

从本质上看，Logistic 方程只有 5 种不同的最大解（考虑水平平移后）：

1. 常值解 $y(t)\equiv 0$, $t\in \mathbb{R}$
2. 常值解 $y(t)\equiv a/b$, $t\in \mathbb{R}$
3. 非常值解 $y_1(t)=\frac{a}{b(1+e^{-at})}$, $t\in \mathbb{R}$（完整的 S 曲线）
4. 非常值解 $y_2(t)=\frac{a}{b(1-e^{-at})}$, $t\in (-\mathrm{\infty },0)$（左半支）
5. 非常值解 $y_3(t)=\frac{a}{b(1-e^{-at})}$, $t\in (0,+\mathrm{\infty })$（右半支）

这些解的值域分别为 $0$, $a/b$, $(0,a/b)$, $(-\mathrm{\infty },0)$, $(a/b,+\mathrm{\infty })$，它们精确地划分了整个实数轴 $\mathbb{R}$。

4. 对称性特征

Logistic 方程的解曲线具有点对称特性。特别地，当 $d>0$ 时，解曲线 $y(t)=\frac{a}{d{e}^{-at}+b}$ 关于其拐点具有点对称性。拐点出现在 $(t_h,a/2b)$，其中 $t_h=(\ln d-\ln b)/a$。

5. 在人口模型中的应用

在人口增长模型中，通常只考虑情况 1 和情况 2（即 $y_0>0$）。在这些情况下：

• 当初始人口 $0<y_0<a/b$ 时（情况 1），人口呈 S 型曲线增长，最终趋近于环境承载量 $a/b$
• 当初始人口 $y_0>a/b$ 时（情况 2），人口单调减少，同样趋近于环境承载量 $a/b$

参数 $a$ 表示无限资源条件下的自然增长率，而 $a/b$ 表示环境承载量。

6. 与收获方程的对比

收获方程（Harvesting Equation）形式为 $y^{\prime }=ay-b{y}^2-h$（$h>0$ 为收获率），是 Logistic 方程的变体。收获方程的渐近行为取决于 $\mathrm{\Delta }=a^2-4bh$：

• 当 $h<a^2/4b$ 时，有两个稳态解
• 当 $h=a^2/4b$ 时，有一个稳态解
• 当 $h>a^2/4b$ 时，没有稳态解（所有解都在有限时间内达到零）

最简单的理解即为考虑 RHS 二次方程根的分布确定函数的导数性质 ->进而确定函数的增长特性

解的唯一性证明

在微分方程 $y^{\prime }=G(t,y)\wedge y(t_0)=y_0$ 的讨论中，我们可以通过以下两种主要方式来证明解的唯一性：

方法一：通过通解结构证明

1. 求出微分方程 $y^{\prime }=G(t,y)$ 的通解，观察到它是一个依赖于参数 $C$ 的函数族 $y_C(t)$
2. 代入初始条件 $y_C(t_0)=y_0$ 确定参数 $C$，从而唯一地确定解

这种方法适用于：

• 一阶线性微分方程（齐次或非齐次）
• 没有稳态解的可分离微分方程

方法二：解的参数唯一性证明

如果解涉及多个参数，需要额外证明同一初始条件 $y(t_0)=y_0$ 不能由对应不同参数的解来满足。

这种方法适用于：

• 有稳态解的可分离微分方程，如 $y^{\prime }=y^2$、$y^{\prime }=t{y}^2$、$y^{\prime }=ay-b{y}^2$

” 不同参数 “ 既指连续的一参数解族，也指 “ 特殊的 “ 稳态解。

Logistic 方程解的唯一性证明

以 Logistic 方程 $y^{\prime }=ay-b{y}^2$ 为例，它有解 $y_{\mathrm{\infty }}(t)\equiv 0$ 和 $y_d(t)=\frac{a}{d{e}^{-at}+b}$，$d\in \mathbb{R}$。

证明步骤：

1. 对于任意 $t_0\in \mathbb{R}$ 和 $y_0\ne 0$，我们可以通过求解方程 $\frac{a}{d{e}^{-a{t}_0}+b}=y_0$ 唯一确定参数 $d$

2. 这表明点 $(t_0,y_0)$ 恰好位于一条解曲线 $y_d(t)$ 上，$d\in \mathbb{R}$

3. 由于 $\frac{a}{d{e}^{-at}+b}\ne 0$，这些解曲线不会与稳态解 $y_{\mathrm{\infty }}(t)\equiv 0$ 相交

4. 这意味着解曲线 $y_d(t)$，$d\in \mathbb{R}\cup \mathrm{\infty }$，将 $(t,y)$ 平面分割开来

以上证明了所有初值问题 $y^{\prime }=ay-b{y}^2\wedge y(t_0)=y_0$ 在给定解函数类中的唯一可解性。

然而，这并不排除可能存在其他形式的解。下面证明确实不存在其他解：

完整证明

可分离方程定理表明，对于点 $(t_0,y_0)$ 且 $y_0\notin 0,a/b$，不可能有两个不同的解通过该点，因此所有不与直线 $y=0$ 或 $y=a/b$ 相交的解已知。

现在假设存在非常数解 $y(t)$ 满足 $y(t_0)=0$（对 $y(t_0)=a/b$ 的情况类似处理）：

1. 不失一般性，可以假设存在 $\delta >0$ 使得 $0<y(t)<a/b$，$t_0<t<t_0+\delta$

2. 由连续性，必须有 $\underset{t\downarrow t_0}{lim}y(t)=0$

3. 但在 $(t_0,t_0+\delta )$ 上定义且在该区间取得小正值的解（必须形如 $y_d(t)$，其中 $d>0$）不具有此性质

4. 这是因为 $y_d(t)=\frac{a}{d{e}^{-at}+b}\to \frac{a}{d{e}^{-a{t}_0}+b}\ne 0$ 当 $t\downarrow t_0$ 时

这一矛盾完成了证明，表明不存在其他形式的解。

$y^{\prime }=\sqrt{|y|}$ 的对比案例

与 Logistic 方程不同，方程 $y’ = \sqrt{

y

}$ 的解不具有唯一性。该方程有：

1. 稳态解 $y(t)\equiv 0$
2. 两个一参数解族：
   • $y_c^{-}(t)=-\frac{1}{4}(t-c{)}^2$，$t\in (-\mathrm{\infty },c)$
   • $y_c^{+}(t)=\frac{1}{4}(t-c{)}^2$，$t\in (c,+\mathrm{\infty })$

这些解共同构成了 $(t,y)$ 平面的划分，使得每个点 $(t_0,y_0)\in {\mathbb{R}}^2$ 恰好位于一条这样的解曲线上。

然而，通过在 $t=c$ 处将 $y_c^{\pm }(t)$ 粘合在一起（以及其他组合），可以得到更多（最大）解，这导致所有初值问题 $y’ = \sqrt{

y

} \wedge y(t_0) = y_0$ 解的不唯一性。

Exact First-Order Equations

定义与基本形式

精确微分方程（Exact First-Order Equations）是一类特殊的一阶微分方程，其标准形式为：

$$M(x,y)dx+N(x,y)dy=0$$

当且仅当存在某个二元函数 $F(x,y)$ 使得：

$$\frac{\partial F}{\partial x}=M(x,y)\text{和}\frac{\partial F}{\partial y}=N(x,y)$$

时，我们称这个方程为精确方程。

这时，方程实际上可以写为全微分形式：

$$dF(x,y)=\frac{\partial F}{\partial x}dx+\frac{\partial F}{\partial y}dy=M(x,y)dx+N(x,y)dy=0$$

精确性的判定条件

函数 $M(x,y)$ 和 $N(x,y)$ 是否满足精确条件，可以通过以下定理判断：

定理：假设 $M(x,y)$ 和 $N(x,y)$ 在区域 $D$ 上具有连续的一阶偏导数，则方程 $M(x,y)dx+N(x,y)dy=0$ 在 $D$ 上是精确的，当且仅当：

$$\frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}$$

这个条件可以通过混合偏导数相等的性质来理解：如果 $F$ 存在，那么 $\frac{{\partial }^{2}F}{\partial x\partial y}=\frac{{\partial }^{2}F}{\partial y\partial x}$，所以 $\frac{\partial M}{\partial y}=\frac{{\partial }^{2}F}{\partial y\partial x}=\frac{{\partial }^{2}F}{\partial x\partial y}=\frac{\partial N}{\partial x}$。

精确方程的几何解释

从几何角度看，精确方程 $M(x,y)dx+N(x,y)dy=0$ 的解是由 $F(x,y)=C$ 表示的曲线族，其中：

• 向量场 $(M,N)$ 与曲线 $F(x,y)=C$ 的任意点处的法向量 $(\frac{\partial F}{\partial x},\frac{\partial F}{\partial y})$ 平行
• 向量场 $(M,N)$ 与曲线 $F(x,y)=C$ 在每点处正交，即解曲线是向量场的正交轨迹

解法步骤

若判断出方程是精确的，求解步骤如下：

1. 构造函数 $F(x,y)$：

   • 从 $\frac{\partial F}{\partial x}=M(x,y)$ 开始，对 $x$ 积分得：

     $$

F(x,y) = \int M(x,y) dx + h(y)

$$ 其中 $h(y)$ 是仅含 $y$ 的待定函数

• 利用 $\frac{\partial F}{\partial y}=N(x,y)$ 确定 $h(y)$：

$$

\frac{\partial}{\partial y}\left(\int M(x,y) dx + h(y)\right) = N(x,y)

$$

 \$\$ \frac{\partial}{\partial y}\int M(x,y) dx + h'(y) = N(x,y)

$$

 因此：

$$h^{\prime }(y)=N(x,y)-\frac{\partial }{\partial y}\int M(x,y)dx$$

 对 $y$ 积分得到 $h(y)$

1. 写出通解：
   • 由于 $dF=0$ 意味着 $F(x,y)=C$（常数）

   • 将 $F(x,y)=\int M(x,y)dx+h(y)$ 代入，得到通解：

     $$

F(x,y) = C

$$

与其他方法的联系

精确微分方程与其他方程类型的关系：

1. 与可分离变量方程的关系： 形如 $g(y)dy+f(x)dx=0$ 的可分离变量方程是精确方程的特例，其中：

$$

F(x,y) = \int f(x)dx + \int g(y)dy

$$

1. 与一阶线性方程的关系： 一阶线性方程 $\frac{dy}{dx}+P(x)y=Q(x)$ 通过乘以积分因子 $\mu (x)=e^{\int P(x)dx}$ 可转化为精确方程

2. 积分因子法： 对于非精确方程 $M(x,y)dx+N(x,y)dy=0$，如果存在函数 $\mu (x,y)$，使得 $\mu Mdx+\mu Ndy=0$ 变为精确方程，则 $\mu$ 称为该方程的积分因子

积分因子法 (Integrating Factor Method)

基本原理

积分因子法是将非精确方程转化为精确方程的技术。对于一般形式的一阶微分方程： $$

M(x,y)dx + N(x,y)dy = 0

$$\mathrm{若}\mathrm{该}\mathrm{方}\mathrm{程}\mathrm{不}\mathrm{是}\mathrm{精}\mathrm{确}\mathrm{的}（\mathrm{即}\$\frac{\partial M}{\partial y}\ne \frac{\partial N}{\partial x}\$），\mathrm{我}\mathrm{们}\mathrm{寻}\mathrm{找}\mathrm{一}\mathrm{个}\mathrm{非}\mathrm{零}\mathrm{函}\mathrm{数}\$\mu (x,y)\$，\mathrm{使}\mathrm{得}\mathrm{新}\mathrm{方}\mathrm{程}：$$

\mu(x,y)M(x,y)dx + \mu(x,y)N(x,y)dy = 0

$$ 成为精确方程。这个函数 $\mu (x,y)$ 称为积分因子。

积分因子的精确条件

积分因子 $\mu (x,y)$ 要使方程变为精确方程，需满足： $$

\frac{\partial(\mu M)}{\partial y} = \frac{\partial(\mu N)}{\partial x}

$$\mathrm{展}\mathrm{开}\mathrm{得}：$$

\mu\frac{\partial M}{\partial y} + M\frac{\partial \mu}{\partial y} = \mu\frac{\partial N}{\partial x} + N\frac{\partial \mu}{\partial x}

$$\mathrm{整}\mathrm{理}\mathrm{为}：$$

\mu\left(\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x}\right) = N\frac{\partial \mu}{\partial x} - M\frac{\partial \mu}{\partial y}

$$ 这是关于 $\mu$ 的偏微分方程，通常难以直接求解。

特殊形式的积分因子

核心均为考虑复杂的偏微分方程的线性齐次形式

仅依赖于 $x$ 的积分因子

当假设 $\mu =\mu (x)$ 仅为 $x$ 的函数时，有 $\frac{\partial \mu }{\partial y}=0$，上述方程简化为： $$

\mu\left(\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x}\right) = N\frac{d \mu}{d x}

$$\mathrm{若}\$\frac{\frac{\partial M}{\partial y}-\frac{\partial N}{\partial x}}{N}\$\mathrm{仅}\mathrm{是}\$x\$\mathrm{的}\mathrm{函}\mathrm{数}，\mathrm{记}\mathrm{为}\$g(x)\$，\mathrm{则}：$$

\frac{1}{\mu}\frac{d\mu}{dx} = g(x)

$$\mathrm{求}\mathrm{解}\mathrm{得}：$$

\mu(x) = \exp\left(\int g(x)\,dx\right) = \exp\left(\int \frac{\frac{\partial M}{\partial y} - \frac{\partial N}{\partial x}}{N}\,dx\right)

$$

仅依赖于 $y$ 的积分因子

类似地，若假设 $\mu =\mu (y)$，则有： $$

\mu(y) = \exp\left(\int \frac{\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}}{M}\,dy\right)

$$

当 $\frac{x^2(M_y-N_x)}{N_y+M_x}=g\left(\frac{y}{x}\right)$ $\mu (x,y)$ 时

$$

\mu’\left( \frac{y}{x} \right) = -g\left( \frac{y}{x} \right)\mu\left( \frac{y}{x} \right)

$$

当 $\frac{M_y-N_x}{N_y-M_x}=g(xy)$ $\mu (xy)$ 时

$$

\mu’\left( \frac{y}{x} \right) = g\left( \frac{y}{x} \right)\mu\left( \frac{y}{x} \right)

$$

4. 积分因子应用步骤

1. 判断方程是否为精确方程：检验 $\frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}$ 是否成立。
2. 若不是精确方程，尝试找积分因子：
   • 检查 $\frac{\frac{\partial M}{\partial y}-\frac{\partial N}{\partial x}}{N}$ 是否仅为 $x$ 的函数
   • 检查 $\frac{\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}}{M}$ 是否仅为 $y$ 的函数
3. 若找到积分因子 $\mu$，构造新方程：$\mu Mdx+\mu Ndy=0$
4. 解新的精确方程：按照精确方程的解法求解。

正交轨线 (Orthogonal Trajectories)

1. 基本概念

正交轨线是与给定曲线族处处垂直相交的另一组曲线族。在微分几何中，正交轨线有重要的理论与实际应用。

如果曲线族 $F(x,y,C)=0$ 是微分方程 $M(x,y)dx+N(x,y)dy=0$ 的解，则其正交轨线族满足微分方程： $$

N(x,y)dx - M(x,y)dy = 0

$$ 这是因为在任意交点处，两条曲线的切向量需要正交。

2. 求解步骤

1. 对原曲线族 $F(x,y,C)=0$ 求微分： 从原曲线隐式方程得到 $\frac{dy}{dx}=f(x,y)$

2. 构造正交条件： 正交轨线的斜率与原曲线斜率的乘积为 $-1$ (正交条件)，即：

$$

\frac{dy}{dx} \cdot \frac{dy}{dx}\bigg

_{\text{正交}} = -1

$$

1. 得到正交轨线的微分方程：

$$

\frac{dy}{dx}\bigg

_{\text{正交}} = -\frac{1}{f(x,y)}

$$

1. 解该微分方程得到正交轨线族

实例分析

求曲线族 $y=C{x}^2$ 的正交轨线。

解：

1. 原曲线的斜率：$\frac{dy}{dx}=2Cx=2\frac{y}{x}$

2. 正交轨线的斜率： $\frac{dy}{dx}{|}_{\text{正交}}=-\frac{1}{2\frac{y}{x}}=-\frac{x}{2y}$

3. 得到微分方程： $\frac{dy}{dx}=-\frac{x}{2y}$ 或 $2ydy+xdx=0$

4. 这是可分离变量的方程： $2ydy=-xdx$，积分得 $y^2=-\frac{x^2}{2}+C_1$，即 $2y^2+x^2=C$

因此，抛物线族 $y=C{x}^2$ 的正交轨线是椭圆族 $2y^2+x^2=C$。

向量场解释

正交轨线的概念可以在向量场中得到自然解释：

1. 微分方程 $M(x,y)dx+N(x,y)dy=0$ 对应向量场 $\overrightarrow{F}=(M,N)$
2. 该方程的解曲线在每点处与向量 $(M,N)$ 垂直
3. 正交轨线方程 $N(x,y)dx-M(x,y)dy=0$ 对应向量场 $\overrightarrow{G}=(N,-M)$
4. 向量 $\overrightarrow{G}$ 在每点处与 $\overrightarrow{F}$ 垂直，因此正交轨线在每点与原曲线族正交