Surface Integral

#Math241

Surface Integration on Curves

Integration with respect to arc length

Motivation

对于相对于曲线弧长的积分，我们希望有对于同一条路径沿不同的方向或不同的参数化结果积分得到相同的结果
我们希望其满足的性质有:

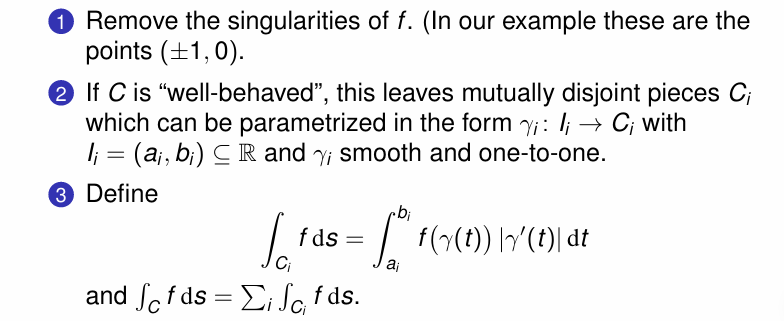
Definition

最终定义相对于 Arc Length 的积分为:

$$ \int_{C_{i}}f\ ds = \int_{a_{i}}^{b_{i}}f(\gamma(t))|\gamma’(t)|dt $$

注意 Integration with respect to arc length 与 Line Integral 的区别

$$ \frac{ds}{dt} = |r’(t)| = \sqrt{\left( \frac{dx_{1}}{dt} \right)^{2}+\dots+\left( \frac{dx_{n}}{dt} \right)^{2} } $$

Parametrized Surfaces

Definition

[!tip] Immersion（浸入）
1. 定义
从 $\Omega$ 映射至 $\mathbb{R}^{n}$ 的可微连续映射，其中定义域 $\Omega \in \mathbb{R}^{d}$ 为开集，当该映射对应的 Jacobi Matrix $J_{\gamma}(u)\in \mathbb{R}^{n \times d}$ 对于任意的 $u$ 均列满秩，此时我们称该映射为 immersion.同时映射对应的值域 $S=\gamma(\Omega) \subset \mathbb{R}^{n}$ 被称为 d 维参数曲面
2. Note

一个参数曲面可以不需在每个点处均为光滑，当出现自交点时我们会有在该点处对应的切线不唯一，导致曲面不光滑

对于 Immersion，我们有在 $\Omega$ 内的任意一个点 $u$ ，由于其所对应的 Jacobi Matrix 均为满秩，我们可以确定 d 个通过该点的参数曲线，通过 Chain Rule 得出其所对应的切向量的集合为包含于 $\mathbb{R}^{n}$ 的线性子空间，即为 Jacobi Matrix 在该点的列空间

对于定义域内的每一个参数 u，我们均可以找到其对应的开邻域使得其在该邻域内对应的参数曲面为 d 维光滑的参数曲面。对于该参数曲面我们可以找到映射 $f:\mathbb{R}^{n}\to \mathbb{R}^{n-d}$,使其对应的 Level Set 即为要求的参数曲面，要求该映射对应的 Jacobi Matirx 行满秩

Notes

Example

Unit Sphere

Surfaces of Revolution
Smooth Curves & Graphs of C1-functions

Smooth Curves：即为 d=1 的情况，对应 immersion 的要求则为其对应的 gradient vector 不为 0
Graphs of C1-functions: 当函数 f 对应的映射为 C1-map,则其函数 f 对应的图的映射也为 C1-map,同时也为 immersion

Differential Manifolds

[!tip] 微分流形
1. 概念
对于 $\mathbb{R}^{n}$ 中的拓扑空间 M，当对于其中任何一个点 a，都存在一个 a 的开邻域 $U$ 以及同胚映射 $\phi:M\to V$ 映射到 $\mathbb{R}^{n}$ 中的开子集 $V$, 使得

$$ \phi(M\cap U) = {x \in V;x_{d+1}=x_{d+2}=\dots=x_{n}=0} $$

此时 M 被称为 d 维微分流形，二元组 $(U,\phi)$ 为一个坐标图 (chart)，一个图册 (atlas) 即为一组坐标图 ${(U_{\alpha},,\phi_{\alpha})}$ 满足每个 $U_{\alpha}$ 为 M 的开子集，且这些开集的并覆盖了整个流形 M
2. 等价浸入 (equivalent immersions)
两个浸入 $\gamma_{1}:\Omega_{1}\to \mathbb{R}^{n},\gamma_{2}:\Omega_{2}\to \mathbb{R}^{n}$ 等价当且仅当存在同胚映射 $T:\Omega_{1}\to \Omega_{2}$ 使得 $\gamma_{1}=\gamma_{2}\circ T$
理解: 等价浸入描述的是浸入映射之间的等价类关系，不同的浸入映射在几何上是相似的，他们通过坐标变换在局部或者全局上彼此转换
3. 性质
对于 d 维微分流形 M 以及坐标图 $\phi:U\to V$

存在浸入映射 $\gamma:\Omega\to \mathbb{R}^{n},\Omega \subset \mathbb{R}^{d}$ 能够参数化 chart region $M\cap U$, 即 $\gamma$ 为双射且 $\gamma(\Omega)=M\cap U$

若 $\gamma_{1},\gamma_{2}$ 均为参数化 $M\cap U$ 的浸入映射，那么 $\gamma_{1},\gamma_{2}$ 等价

Definition

Example

等价浸入 & d 维微分流形性质

Volume of d-Dimensional Parallelepipeds

Definition
在 $\mathbb{R}^{n}$ 中有一组向量确定的平行多面体定义如下,同时我们希望定义其体积满足如下性质:

Theorem(体积定义)

证明这样定义的体积满足要求

Integration over a chart region

Motivation

核心想法: 我们希望将函数 $f$ 定义在 $\mathbb{R}^{n}$ 中 d 维微分流形上 $M$ 的曲面积分通过其参数化映射以及函数 f 的复合转化到 $\Omega$ 上一般勒贝格积分 ->但是我们不能直接用函数 $f$ 及其参数化 $\gamma$ 的复合
通过研究线性映射下体积的改变 ->利用微分推广到非线性的一般情况，同时引入 Gram Determinant 来量化体积的改变

Definition

最终我们得出 Integration over a chart region 的定义

$$ \int_{M_{0}}f \ dS = \int_{\Omega}f(\gamma(u))\sqrt{ g^{\gamma}(u) }du $$

其中 Gram Determinant $g^{\gamma}(u)$ 定义为

$$ g^{\gamma}(u)=\det(J_{\gamma}(u)^{T}J_{\gamma}(u)) $$

特别地，该曲面定义不依赖于参数化映射的选取

Example

Volume if the slotted unit sphere
Volume of a torus
important example
Integration over graphs
Important Application

对于 $z=f(x,y)$ 的简单情况，该映射的 graph 本质上为三维空间的内的二维微分流形，我们有如下公式计算其在该 graph 上的曲面积分

Integration over Manifolds

Surface Volume

Integration over $C^{1}-$Surfaces

Definition

Examples

Differential Forms

Alternating Forms

[!tip] Alternating K-forms
定义：设 $V$ 是一个维数为 $n$ 的向量空间，其基域与 $K$, 一个 k 线性映射 (接受 k 个向量作为输入) 称为 k- 形式：

$$ \omega :V^{k}\to K $$

如果这个映射满足交替性，则称其为 alternating k-form
性质

对于每个输入向量满足线性

交替性：输入的 k 个向量任意两个向量相等时， $\omega$ 的值为 0,等价于交换任意两个输入向量时， $\omega$ 的值改变符号

Definition

Wedge Product of linear forms

外积

[!tip] Wedge product
1. 定义
对于线性形式 ($\mathbb{R}^{n}\to \mathbb{R}$ 的映射算子) $\phi_{1},\dots \phi_{k}$, 我们定义其 wedge product $\phi_{1}\wedge \phi_{2}\wedge\dots \wedge \phi_{k}$ 为其各个映射接受所有 k 个输入向量的行列式
根据其定义，我们易知其满足 alternating k-form 的要求
2. 对偶基
对偶基 $dx_{1},\dots ,dx_{n}$ 为对偶空间 $(\mathbb{R}^{n})*$ 中的一组线性形式，满足：

$$ dx_{i}(e_{j})=\delta_{ij} $$

当 $i=j$ 时， $\delta_{ij}=1$, 否则为 0
核心性质： $dx_{i}(v)=v_{i}$

$$ dx_{i}(v)= dx_{i}(\sum_{k=1}^{n}v_{k}e_{k})=\sum_{k=1}^{n}v_{k}dx_{i}(e_{k})=v_{i} $$

3. 对偶基的楔积
$dx_{i_{1}}\wedge\dots \wedge dx_{i_{k}}$ 的楔积，其中 $1\leq i_{1}<\dots<i_{k}\leq n$ 构成 $Alt^{k}(\mathbb{R}^{n})$ 的基底，我们有
dim $Alt^{k}(\mathbb{R}^{n})=C_{n}^{k}(0\leq k\leq n)$
4. 微分形式以对偶基楔积为基底表示

$$ \omega=\sum_{1\leq i_{1}<\dots<i_{k}\leq n}\omega(e_{i_{1}},\dots ,e_{i_{k}})dx_{i_{1}}\wedge\dots \wedge dx_{i_{k}} $$

对于任意两个微分形式 $\omega \in Alt^{k}(\mathbb{R}^{n}),\eta \in Alt^{l}(\mathbb{R}^{n})$ ，他们的楔积满足

$$ \omega \wedge \eta=(-1)^{kl}\eta \wedge \omega $$