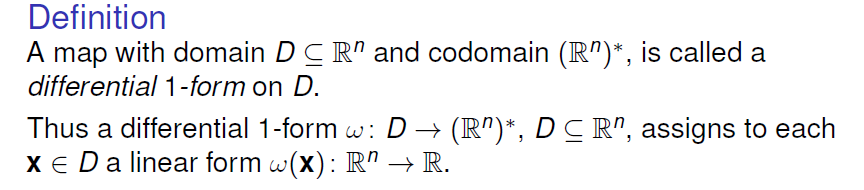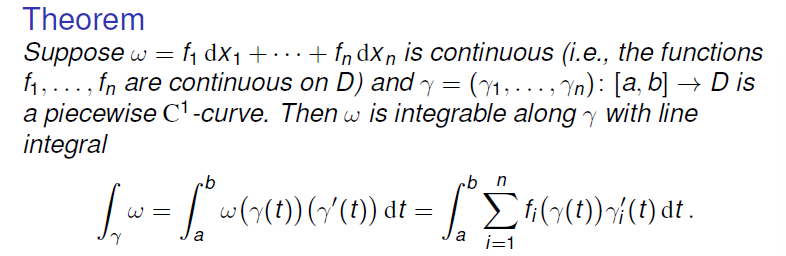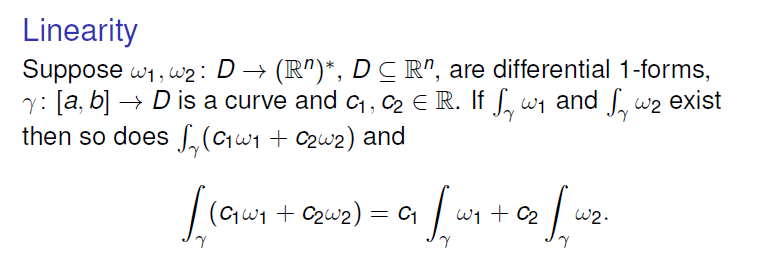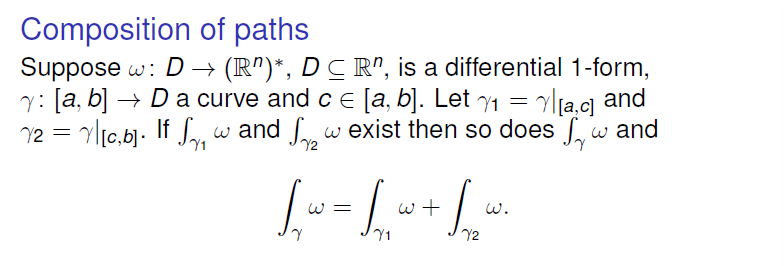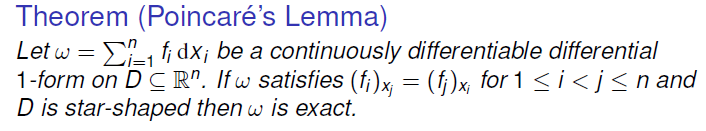Vector Analysis

#Math241

Vector Fields and Differential Forms

Vector Fields

1. Definition

[!tip] Definition
A Vector Field is a mapping $F:D\to \mathbb{R}^{n}$ with domain $D \subset \mathbb{R}^{n}$
向量场即为对 n 维空间中的每一个点赋上一个 n 维向量

2. Example

注意 Gradient Field 定义，核心即为向量场对应的向量函数可以表示为一个函数的 gradient，在这种情况下，该向量场为保守向量场，其路径积分仅与起点与终点有关

Differential 1-Form

回顾 Linear Form

Linear Form 即为对 n 维向量进行点乘，从 $\mathbb{R}^{n}$ 到 $\mathbb{R}$ 的线性映射

Definition

[!tip] 对偶空间 $(\mathbb{R}^{n})*$

基本定义
给定一个向量空间 $V$,其对偶空间 $V^{}$ 为 $V$ 上所有线性映射的集合。因此， $V$ 中的元素为将 $V$ 中的每一个元素映射到实数的一个函数，且满足线性条件

$\mathbb{R}^{n}$ 的对偶空间
当 $V=\mathbb{R}^{n}$ 时， $\mathbb{R}^{n*}$ 表示的是从 $\mathbb{R}^{n}$ 到 $\mathbb{R}$ 所有线性函数的集合，这些线性函数通常被称为线性泛函。
记 $\mathbb{R}^{n}={x=(x_{1},\dots,x_{n})}$, 那么一个线性泛函可以表示为

$$ \phi(x) = \sum_{i=1}^{n}a_{i}x_{i} $$

其中 $x \in \mathbb{R}^{n}$

Differential 1-Forms 即为对定义域中的每一个向量都找到一个线性泛函，为从定义域到其对偶空间的映射；也可以理解为一个向量场,对定义域中的每一个元素都有一个对应的向量进行映射

Standard Representation

Complex Differential 1-Forms

Line Integrals

Motivation
研究 Line Integral 的 Motivation 来源于物理中希望沿某一条确定的路径在空间中积分得到做功

Tagged Partition
即为带标记的划分，常用在进行黎曼积分类似的分段积分中，用于标记区间中的元素

Definition

Properties of Line Integrals

Some Terminology
将曲线轨迹参数化后积分
Theorem
线性: Linearity
Composition of Paths(将路径不同段相加)
重新参数化

注意从不同的方向对 Line Integral 在一条给定的曲线上积分的得到结果可能正负相反（例如交换起点与终点）

Example

Winding Curve
考虑利用 Normalized Curve 绕原点的圈数考虑 Line Integral 的值

为了计算绕行的重数，我们引入Winding Number(绕数)

Fundamental Theorem for Line Integrals

Gradient Field(Conservative Field) 的性质

[!tip] Exact Differential 1-Form（全微分 1- 形式）
1. 定义
对于一个 Differential 1-form $\omega:D\to (R^{n})^{*}$, 当存在一个函数 $f:D\to \mathbb{R}^{n}$ 满足 $\omega=df$ 或表述为其对应的 Vector Field 为 Gradient Field, 那么我们称改 Differential 1-Form 为 exact(全微分)
2. 必要形式（闭形式）
在给定区域内，如果 $\omega$ 为全微分，则其外微分 (exterior derivative) 必须为零：

$$ d\omega=0 $$

3. 充分条件 Poincare’s Lemma(庞加莱引理)
如果区域 $U$ 是单连通 (simply connected),并且 $d\omega=0$, 则 $\omega$ 为全微分形式
4. 性质

保守性：沿任意路径的线积分只取决于路径的起点与终点

$$ \int_{C}F \cdot dr=f(B)-f(A) $$

路径无关性：如果向量场为全微分的，那么在场内的路径积分是路径无关的 (Path-Independent)->这意味着闭合路径的积分为零

零旋度 (Curl-Free Property)

$$ \nabla \times F=0 $$

Proof: 通过其 Gradient Field 的性质，参数后以后将其转化为单元函数 ->利用微积分基本定理

Corollary

Converse of the Corollary

Independence of path implies exactness

Oberservations

Connected Subsets（连通子集）->该子集不能够被划分为非空的不交开集

Theorem

对于定义在连通开集上的连续微分 1 形式，它为全微分当且仅当其积分与路径无关

Example->通过 $\omega$ 的形式通过积分找到其反函数

Locally Exact 1-Forms

Definition

Locally Exact->考虑 $\omega$ 在对应的邻域范围内为全微分形式

Proposition: Locally Exact 的必要条件 ->考虑 Clairaut’s Theorem

关注函数对应的偏导是否相等

简单的例子

Curl and Divergence

散度 (Divergence) 与旋度 (Curl)

Definition

简单的记忆方式:

旋度理解为：向量场与 Gradient 算子的叉乘，旋度仍然为三维的向量场
散度理解为：向量场与 Gradient 算子的点乘，散度则为实值函数

散度与旋度的性质

Poincare’s Lemma

[!tip] Topology Terms
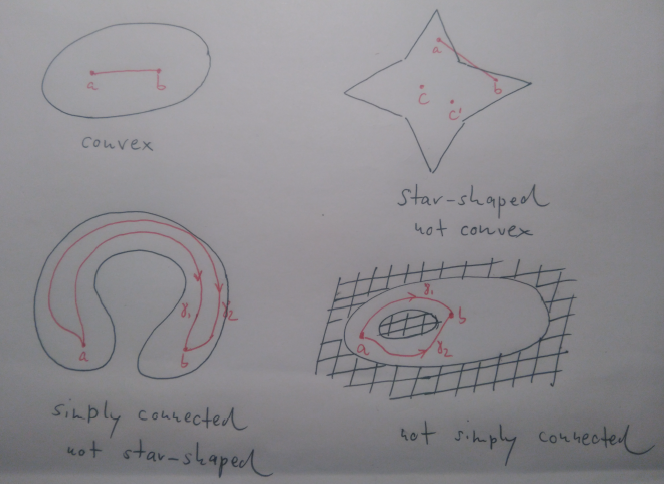
1. 凸集
一个集合被称为凸集如果对于集合中的任意两个点 $x,y\in S$, 连接着两个点的线段全位于该集合中。这意味着:

$$ \lambda x+(1-\lambda)y \in S,\lambda \in[0.1] $$

2. Star-Shaped Set（星形集）
一个集合被称为星形集，如果存在一个点 $x_{0}\in S$,使得从该点到集合中任意点 $y\in S$ 的线段都位于该集合中
从几何直观上，星形集允许局部的凹陷，但必须存在一个“星心”(也可以有多个)
3. Simply Connected Set
一个集合是单连通的，如果对于任何闭合曲线都可以连续收缩成一个点而不离开集合
4. Not-Simply Connected Set（非单连通集）
一个集合是非单连通的，如果至少存在一个“洞”，使得一些闭合曲线无法在该集合内连续收缩成一个点