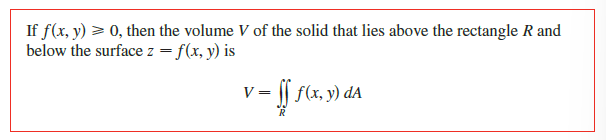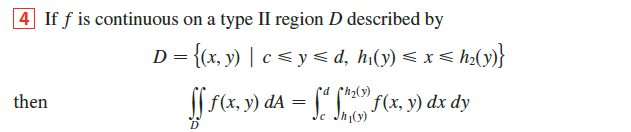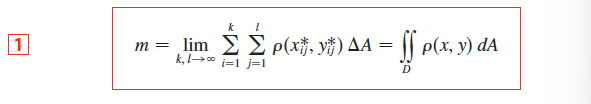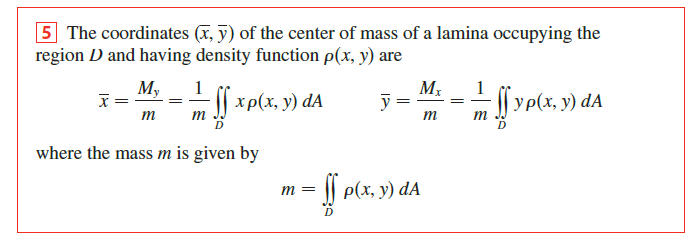#Math241

Riemann’s vs Darboux’s Definition

Riemann’s Definition
e19df146390d2e7c9f3cfb183aa8b3c.png

Darboux’s Definition

  • 先定义 Darboux Sums->考虑在有限区间划分时定义分段的上下界和
    0db7b402993eb818b11a131623d5c03.png

  • 进一步地，我们验证其性质 ->随着划分变细，下界与上界和不断逼近

3047c5bd1b192436e2999c5fd9f5bf1.png

  • 最终统一 Riemann definition 与 Darboux Definition
    f84064392137828d8edfc2aab6396eb.png
    09f4fc19c7ce4afb073b640e9ed3996.png

Problems

75877dac5e4bc365b0c22b78fd1c049.png
Example

  • 迪利克雷函数 ->非黎曼可积（上下界无法逼近）

128ef0d80fcf7d2b03a46d9fad5bf76.png

  • 对于 Unbounded 的情况 ->虽然非黎曼可积，但有时可以定义 improper integral

a26ee38b0ed7c59b30702ffc703d215.png

Continuous Function

Uniform Continuity

定义在闭区间上的连续函数一定一致连续（或表述为定义在紧集上的连续函数一定一致连续）

c80360c5556a3402de64b59fe954c19.png

Theorem
任意连续函数均为黎曼可积
5d81369694c2b99dc5ad40fefa9a9a0.png

Higher dimensional Case

394cce6cf7c1c5aecbaee7a2feb8d5a.png

cd615ece6d2668aab33afa783505622.png

472744cf81118f40c4f354b95d08097.png

将对应的 Riemann 与 Darboux 的积分定义推广到 n 维 ->考虑采取笛卡尔积

  • 一维区间转化为各个维度对应区间的笛卡尔积（形成一个超长方体）
  • 对于单一区间的分割转化为在 n 个维度上的区间分别分割（注意分割的份数和尺度可以不同）,最终形成 N1…Nn 个子区间
  • 区间长度转化为对应划分区间的 volume
  • Riemann Definition 的 mesh size->任意子区间的最长长度
  • Darboux Definition 的上下界和 ->对应分割处的超长方体体积乘该区域内函数的上下界
  • n 维积分为线性

c3f4a3e0265ac9bea827c980c4f7438.png

Iterated Integrals

核心思想：将 n 维情况的积分化归到一维 ->Little Fubini Theorem

Throrem 富比尼定理

a3737b3090f3d52c647d0f0efbd2b3c.png
固定剩余变量，不断进行一维积分得到最终结果

注意要求：在给定区域上可积

Proof

证明思路：
将新定义的函数夹逼在原有 Darboux Sum 之间

2fe8a0736a1f2705820dad33ff82881.png

5f9c6bdbbaf4a5627fb02fa1064f7b7.png

Application

1. 推论：将重积分分解为两单维变量的积

70efcc69034e19aa15a38b09f192a05.png

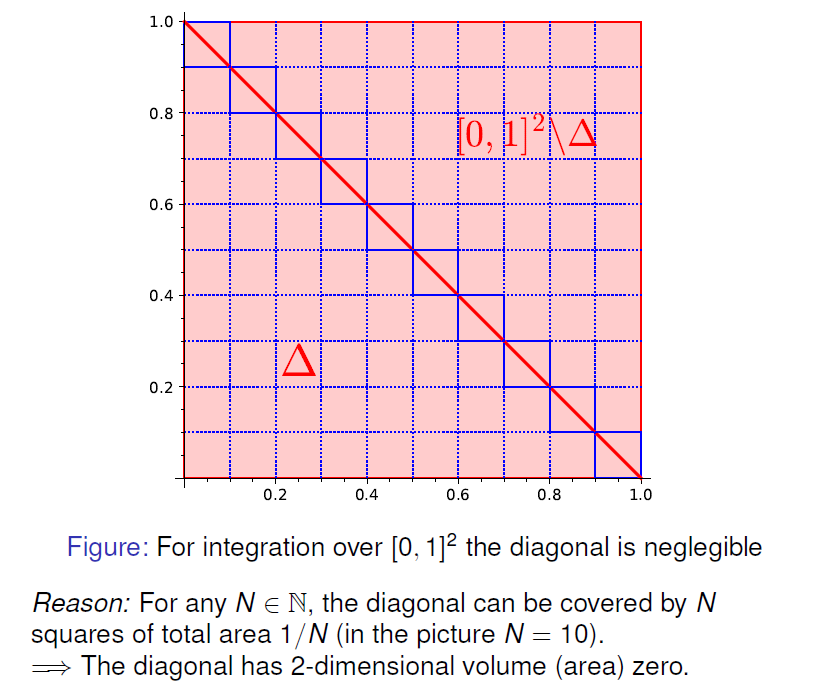
2. 当被积区域非矩形时，考虑扩展出一个矩形区域，将非定义域内部分的函数值设为 0

[!tip]
上述定义基于将定义域划分为多个矩形，如何将其推广至更广泛形式的限制域？

此时只要在整体划分的矩形区域上可积，即可用 Fubini 定理

Example

4526bb75eac68a4a7426ecc2fe6bd65.png

c9697d2b6c54a4b098a365eef333084.png

考虑对扩展定义形成的不连续区域进行放缩估计，最终控制达布和上下界之间的差距

Application & Example

进行重积分的一般步骤

  • 确定待积区域，关注变量之间的相互限制关系，考虑相对较简单的内层函数积分选择
  • 确定待积函数，可适当考虑其几何意义，想象位于被积区域上方的一个曲面
  • 对于特殊函数关注其对称性进行简化

Volume

316beebcfbfb7d9672a79f32c82c352.png

351a99e8f0657f672cba874c12d029e.png

6880c76f9158f7c61a74356a42c3c3f.png
7331196f6e303ce59e7e832b8158d96.png

对于利用 Fubini 定理进行重积分的形象理解
考虑固定其余变量，则内层积分即为积分求解对应截面的面积，然后外层积分再把每一层对应的面积整体积分形成体积

Area

计算 R2 某一个区域内的面积

  1. 重积分（原理为考虑底面积为 Area(D) ,高为 1 的几何体）
    • 令 f(x,y)=1
    • 对于给定区域 D 进行重积分
  2. 单变量积分

Polar Coordinates Change

利用极坐标换元处理约束问题
5dd30382747aa2cd33144299a9f0b7f.png
8a8201d3754da4c3466327533c2df62.png

Average Value

Average Value 定义即为对于给定区域的重积分除以该区域对应的单位体积（面积）
9497134fb93f3b31ecb847b794732fb.png

Mass, Moments and Centers of Mass

  • Mass: 考虑对单位面积分别对应的密度积分
    8c7949ce203bd3e6fd9c021c36f3eed.png
  • Moment
    391f36193132b7333cf281fe4338ce0.png
  • Center of Mass
    e44b567738f352db82cd72800792724.png

对于轨迹的 Center of Mass 来说，我们有
465d127c956f2e42600805840bb3701.png

  • Moment of Inertia
    转动惯量
    8314e8417a6ac6ea558bee93b182327.png

Centorid

Definition

质心的定义即为对于每一维上的在给定区域的积分与该区域单位体积的比值

s=1Vol(D)(∫Dx d2(x,y),∫Dy d2(x,y))

其中 Volume(D) 定义如下，即为给定区域的单位体积（二维时可以理解为面积）

Vol(D)=∫D1 d2(x,y)

对于一般的 n 维情况，我们有

si=∫Axi dnx∫A1 dnx

Surface Area

核心即为考虑利用切平面对连续的曲面面积进行近似，再进行积分
根据偏导的结果计算出曲面在每个点的切平面面积

49a0f3c4eb4d80a03dcf0c16a4a8fff.png

3ac290e86ce03704b26b08ac20c0019.png

Triple Integral

Cylindrical Coordinates

柱坐标系表示
8c49e097f4a5c81ce6ad93c9252e038.png
将 z 用 x,y 表示的函数约束,同时用极坐标换元表示 x,y 所在区域，注意勿遗漏 r

9354a4cf528032d9bae5ae5f56d5586.png

Spherical Coordinates

球坐标系表示
2576d51c2e9ddc5170ae28f497c458f.png

**换元积分 ->注意换元后的行列式绝对值为 ρ2sin⁡(ϕ)

5b2e23a61e979a6c03f4ff6c2867107.png

常用于处理积分限制域由球面或者圆锥面限制的问题

Further Problems of Riemann Integrals

[!danger] Problems

  1. 黎曼积分所要求的矩形区域对于一般的重积分问题往往不具有泛化性，不便利
  2. 对于高维空间中多个子集的积分应该有更好的定义，而非只局限于黎曼积分所要求高维矩形区域
  3. 在欧几里得变换下体积应该保持不变性，但是当进行正交变换移轴后集合体整体轴不与原坐标轴平行，无法利用黎曼积分所定义的矩形区域积分
  4. Fubini 定理在一些情况下可以适当泛化，放松对函数性质的要求

对于积分区域要求严格的解决方案 ->引入勒贝格积分Lebesgue Integral

68998eea57a49a77d279fa597d1e722.png
4af52afe1e6a79ea96f5a422057b8ce.png