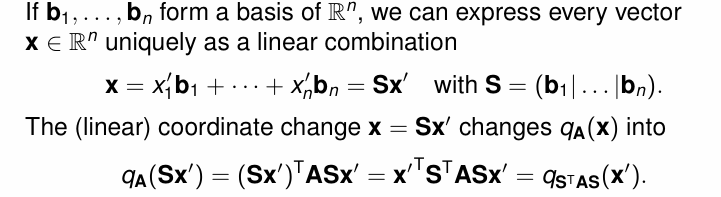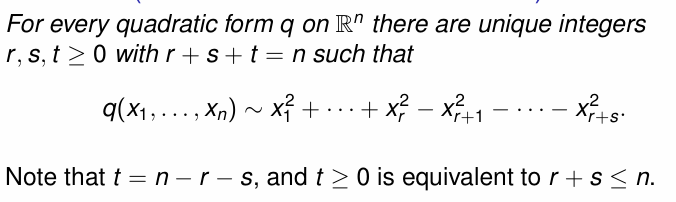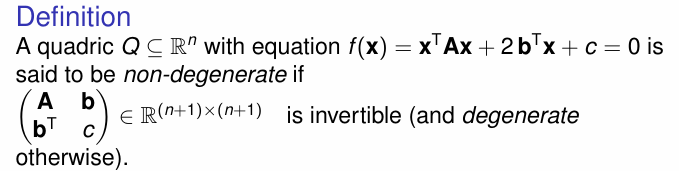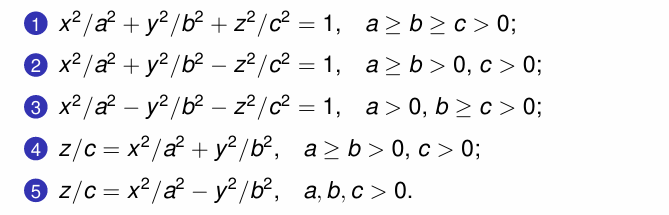#Math241

Related Topic: 二次曲线，谱定理

[[ Coordinate System#Quadric Surfaces(二次曲面) ]]

Quadratic Forms

Concept

  • 二次型与正定矩阵定义

9a81f218cfd35fb4b441a36f0c82bcb.png

  • Coordinate Change

211b82adc2ca86ec5fa4366091494ea.png

  • 等价二次型 ->能够通过引入一个可逆的线性变换矩阵在两个二次型对应的矩阵之间进行转化

7dcdc020723e93ef1ce47332236c7e8.png

$$ B = S^{T}AS $$

Theorem

[!tip] Sylvester’s Inertia Theorem

  1. 任意实对称矩阵均可以通过正交变化对角化，对角化过程中其特征值的符号不会发生改变，对应特征值的系数记作惯性系数
  2. 或表述为任意一个实对称矩阵均可被表示为一系列线性独立变量的平方和，系数为正负 1

491b664c74be26ca5d129aa7d24e6bb.png

核心为任意一个二次型可以经过可逆矩阵的转化得到正则态 ->消除交叉项

Observation

  • SYLVESTER’s Inertia Theorem 意味着任何一个表示二次型的矩阵都可以被变换为如下的对角阵

$$ \begin{pmatrix} I_{r} & &
&-I_{s}
& & 0_{t} \end{pmatrix} $$

  • 可以通过其正则形式轻松确定二次型对应的矩阵是否正定，即直接通过其特征值判断二次型是否正定

Quadrics and their Classification

Definition

e0e31b736d21508e9cb0a679a0c870b.png
Quadric（二次曲面）即为 n 维二次实系数多项式对应的解集

Example

  • $\mathbb{R}^{n}$ 中任意的仿射子空间为 Quadric
  • $\mathbb{R}^{3}$ 中两个独立的平面也可以构成二次曲面

  • $\mathbb{R}^{3}$ 中的二次曲面可以由 $\mathbb{R}^{2}$ 中的圆锥曲线变化得到
    1cb8623aa4f5f29a9a50acc73c18056.png

  • 考虑如下 $\mathbb{R}^{3}$ 中非退化的情况：
    d3a694cf686081019c2aada778fd3e6.png
    注意双曲线体的叶数由系数中负数的数目决定

General Quadric

de9421ba4d7bbb912f170505d5a72c0.png

任意一个二次曲面可以用如上线性方程的形式表示

  • 特别地，当二次系数对应的对称矩阵可逆时，我们可以找到相应的仿射变换使一次项为 0，此时我们说对应的二次曲面是中心对称的

平移向量 $v$ 通过求解：

$$ v^{T}A+b^{T} = 0 $$

注意对于如上方程求 gradient 结果为：

$$ \nabla f(x_{0}) = 2Ax_{0}+2b $$

Classification

Non-degenerate Form 非退化的二次曲面

  1. 定义：
    1995abed03c65254f1911db3942607f.png

考虑二次多项式全体系数构成的对称矩阵是否可逆

另一表述方式为考虑该二次曲面的projective extension（射影扩展），该射影扩展无奇异值（即引入一个新的维数，将一次项升维成二次项）
有奇异值的地方无 Tagent Plane(Gradient=0)

7649f0730c8b0750ba6d478cc8bed2c.png

  1. Example
    以下例子提供了一部分退化二次曲面的分析，对于这些退化的二次曲面
    • 一部分我们可以直接通过其原始定义发现其中的Singular Point（奇异点，gradient=0,没有对应的切空间）
    • 另一部分我们可以通过考虑射影空间，关注原曲面与无穷远点的交集

234a50a8706f5bfec9bc56986ca18e3.png
3ff52a5a36e588ce202c063f0c4a664.png

  • 注意圆锥的定义：

$$ x^{2}+y^{2}=z^{2} $$

[!tip] 常见的退化情况

  1. 圆锥
    可以化简为 $z^{2}=x^{2}+y^{2}$ 的形式，由两个 length function 拼接而成，其中原点为 singular point
  2. 两平面的并集（平行或非平行）
    $(\alpha_{1}x+\alpha_{2}y+\alpha_{3}z+\alpha_{4})(\beta_{1}x+\beta_{2}y+\beta_{3}z+\beta_{4})=0$,他们的交线（考虑无穷远点）即为 singular point 的集合
  3. 圆柱面
    形如 $x^{2}+y^{2}=1$

Theorem

对于非退化的情况，根据矩阵 A 的秩，我们可以分为两大类
ca84248c9bbce1393a0d79a0443b448.png

[!tip] 对于三维空间中非退化的二次曲面

  1. 二次系数矩阵 A 满秩 ->此时二次曲面中心对称，我们可以找到相应的仿射变换将其转化为球面或双曲线体（一叶或两叶）
  2. 二次系数矩阵 A 秩为 2->此时二次曲面非中心对称，我们可以找到相应的仿射变换使其转化为椭圆抛物面或双曲抛物面

补充

  1. Elliptic Paraboloid 椭圆抛物面
    形如 $z=x^{2}+y^{2}$ ，其沿轴方向的截面为抛物线，垂直于轴方向的截面为椭圆
  2. Hyperbolic Paraboloid 双曲抛物面
    形如 $z=x^{2}-y^{2}$ ，其沿轴方向的截面为抛物线，垂直于轴方向的界面为双曲线

证明
6cbef8a1f5676eb404230318514b762.png
56a7deeec7b2f9f5350ee553b643c55.png

综上，对于 $\mathbb{R}^{3}$ 中任意非退化二次曲面，我们可以分为以下五类
9f320d18fbbfa9332a54935caf591d6.png

  1. ellipsoid
  2. hyperboloid of one sheet
  3. hyperboloid of two sheets
  4. elliptic paraboloid
  5. hyperbolic paraboloid

[!tip] 一般简化过程

  1. 通过全体系数构成的对称矩阵确定是否为退化情形

  2. 对于非退化情形，根据二次系数矩阵确定是否为中心对称：

中心对称，A 满秩，求解 Av+b=0 得到曲面中心，再通过平移变换减去，此时二次曲面的一般形式表示三个变量均为 2 次，对应上述分类 1-3 （惯性系数均非 0）

非中心对称，A 不满秩，直接换元 z 为后续所有一次项与常数项，得到最终表示，此时二次曲面的一般形式表示有一个变量为 1 次，对应上述分类 4-5（存在一个惯性系数为 0）

  1. 进一步地通过合同变换或特征分解得出其正则形式

补充：合同变换过程
求任意二次型矩阵的合同变换 - 知乎
核心想法为通过初等行变换以及所对应的列变换将矩阵化为对角阵，合同变换的过程不会改变最终对角线上元素的符号

考虑将 A 与 I 拼凑形成增广矩阵，然后对 A 进行相应行变换与对称列变换形成三角阵，I 记录过程中的变换系数
cfb1480e9d647f02633267d47a9bdf5.png

最终对应的变换为:

$$ x = Cx’ $$

  • 注意，当起始对角线上元素为 0 时注意先进行行变换使主元不为 0

  • 已经化为对角阵后，如果进行倍乘变换，注意由于此时也需要对行列各操作一次得到 1，所以选择的倍乘系数为当前开根号

Principal Axes Theorem(谱定理)

任意对称矩阵的均可通过正交阵特征分解为对角阵

c41a496345504be19c47610f62643e2.png