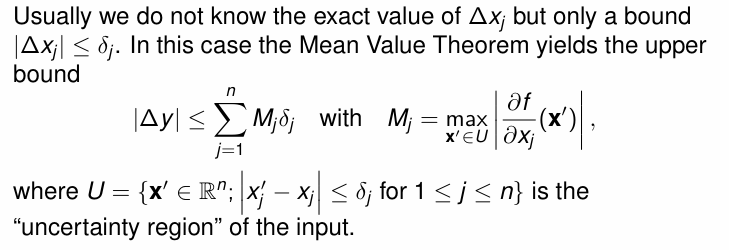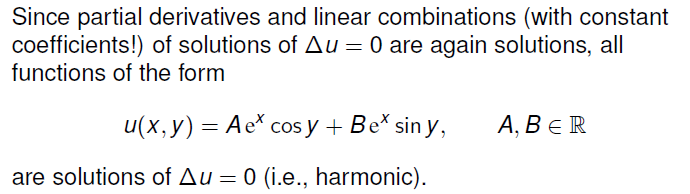#Math241

Mean Value Theorem and its friends

Theorem

857e0f79cabc1a5e287bade3ef66a27.png

通过构造一个单变量函数 $\phi$ 构造从 $[0,1]$ 到对应 f 路径内点的映射，结合一维的 Mean Value Theorem
注意起点与终点所遍历的点都需位于定义域内

Integral Version

9a81bcfd521d81373eaa74db49b7080.png

Another Theorem

b1bdbb4c2b0557cee7a6269983b1129.png

  • Path-Connected:
    对于域内任意两点，均存在一条连续的曲线满足 $g:[0,1]\to D,g(0)=a,g(1)=b$

Example:
对于凸集，集合内任意两点的连线仍然位于集合内

  • 注意 Path-Connected 并不一定意味着 D 中没有 holes, 表示的是对于定义域中任意两个点，都可以找到一条连续的路径历经定义域中的点将其相连
  • 证明只需考虑 m=1 的情况（因为各分项均为常数，同理）
  • 证明利用 Mean Value Theorem 的积分形式，不失一般性考虑一个 smooth 的函数

8be46319e6723c331f116a3cfb5a27b.png

Intermediate Value Theorem 介值定理

d122379be45e756827869cd2b0d5433.png
注意介值定理的泛化表述告诉我们对于一个连续的函数，从一个连续的区间可映射到另一个连续的区间

Path-Connected and Connected

03aadb241ec8fd19fea085c10be2d42.png

[!tip] Path-Connected 与 Connected

  1. Connected 连通
    一个拓扑空间或集合是连通的，如果它不能被分成两个互不相交的非空开集。即如果集合 $X$ 是连通的，那么不存在非空开集 $U,V$,使得 $X=U \cup V$ 且 $U \cap V = \emptyset$
  2. Path-Connected 路径连通
    一个集合 $X$ 是路径连通的，如果对于集合中的任意两点都存在一条连续的路径。也就是说存在一个连续的映射 $f:[0,1]\to X,f(0)=x_{1},f(1)=x_{2}$
  3. 关系
    路径连通一定连通，连通不一定路径连通

Application-Error Propagation

8648f45904dc0686f15765a356f7225.png

利用 Mean Value Theorem 将模糊的小 o 表示转化为精确的数值
Mean Value Theorem 可直接将对应增量的结果转化为 ->起点与终点线段上某点的导数

实际应用中往往用于控制上界，因为往往只能控制住误差的上界

求解过程中：

  • 关注对应每个变量误差的上界
  • 每个对应变量偏导在对应超矩形范围内的上界（绝对值）
    9a4271b31f39df37b61da8df5343633.png

误差分析的 Example: 注意课本没有涉及 Mean Value Theorem，通过考虑 Mean Value Theorem 对上界进行更好的估计
7086493b43e1f772c3a060dbde82a65.png
e79102d68fe814e3f62fe6869b73c37.png

Relative Error

Approximate Form

19f9c296469fdad9126277a0da15a65.png

将整体写成 $\frac{\Delta x_{j}}{x_{j}}$ 的形式更容易看出相对误差

Rigorous Estimate
ec4590f9f0b81f1fde653a9e3a7bdd5.png

Floating-point Numbers

Definition
b21d64bf447939b0b2c617a88275847.png
Precision when taking standard arithmetic functions
对于减法，浮点运算不是良定义的，因为无法控制其相对误差的上界

Implicit Differentiation

4b66433bec5afe1335e19a1190aadae.png

之前在利用 Chain Rule 研究 gradient 与 countour hypersurface 时，我们发现两者的垂直关系，现在我们可以利用这一关系，确定之前隐式定义的从 (n-1) 维到 (n) 维的参数化的映射

Example

给定

$$ F(x,y,z)= x^{3}+y^{3}+z^{3}+3xyz $$

我们考察其的 Coutour

$$ F(x,y,z) =1 $$

在添加了一个限制条件后，我们即可以对原有的三维自由变量进行降维（考虑自由度的变化），因此，我们可以找到一个映射 g 对原有三维变量进行 Parametrization

$$ F(x,y,g(x,y)) = 1 $$

那么我们可以根据 Chain Rule 考察我们隐式定义的映射的偏导情况
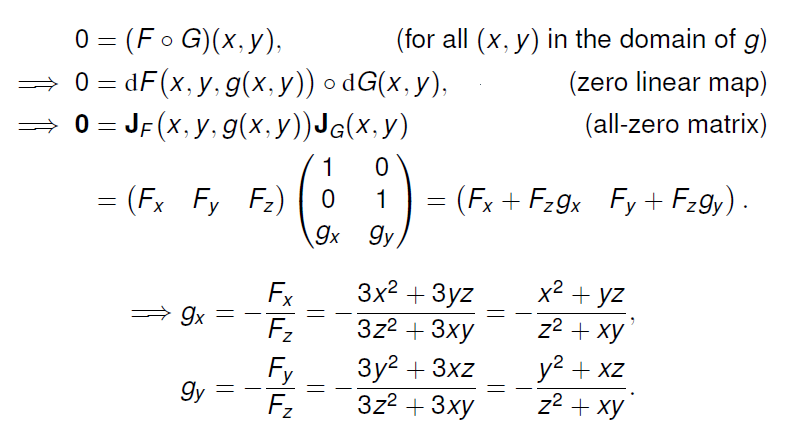
3e3c9631cbf85c75a6d09581624cd86.png

进一步地，我们考察这个隐式定义的函数的定义域的情况

  • 为什么会有定义域的问题？->考虑到对曲面参数化的过程中，有时会出现无法满足函数定义的情况，那么我们需要对整体参数化的函数定义域进行一个划分或者邻域的限制，使其可以满足条件
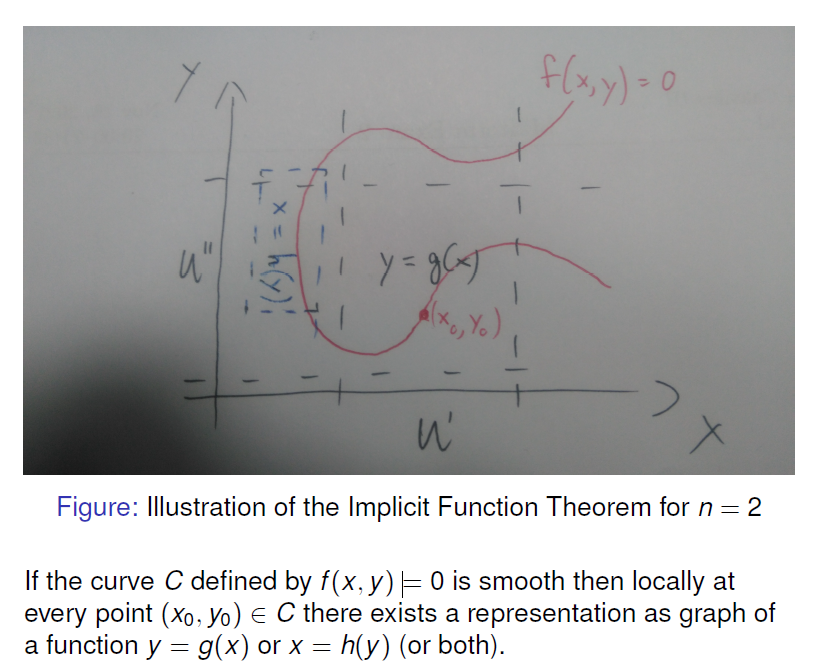
    efdca5660f94bc223685ca030fc0039.png
  • Implicit Function Theorem

de23692f735ddc943747c1c8dfd6ba5.png

Higher Derivatives

考虑高维的微分时，将对于每一个变量求偏导视作一个映射或算子，输入为函数，输出也为函数
8a03e459e8fa59c7f22d4d54f155673.png

注意记号：

$$ D_{j} = \frac{\partial}{\partial x_{j}} $$

从函数到函数的映射

Clairaut’s Theorem

8120188a619bbee70ab2ab66d71233d.png

关注简单的应用，记为
对于高阶偏导，可以置换具体求偏导的过程变量，仍不改变最终结果

证明：
构建一个二阶差分，然后利用 Mean Value Theorem 进行化简，从两个顺序分别看求偏导的结果

2ee8ca604aa6f0c87e4fabc8ff16048.png

Partial Differential Equations(PDE)

Laplace’s Equation

aeeabd11cd072d0b480f2cd05fc57e3.png

$\Delta$ 为 Laplace 算子

  • 二维 Laplace 方程的解：可以对特解采取线性组合
    985ad1d35f18aaa35e0f1b8ff3e7d3a.png

注意 Harmonic Function 的定义:Laplace 算子恒为 0

  • 具体的求解过程

e1d101b5be33a249f74d5553c891bec.png

对于特殊情况，想考虑将最终映射可以分解为两个独立于 $x$ ,$y$ 函数的映射，然后独立求解

  • 建立与复指数的联系
    9b672c4938a305c4068685579ab16ed.png

Complex Differentiable<->Holomorphic（可复微分的函数即称为全纯函数）

Example: 利用复数确定什么样的多项式函数为 Harmonic
6598d4e4aeefab9067a67af0933a993.png

Wave Equation

d0908c1a19437bfb39704374677f98b.png

Optimization

Overview

Types of Problems
aa12d207b1ed7a5c2ff2eeed4e5df63.png

Terminology

  • Optimization Problem: 对于给定的实值函数，在定义域的确定子集 $S$ 上寻找其最值
  • Feasible Solution: 对于任意属于可行域 $S$ 的元素 $x$, $S$ 为可行域 (feasible region), $x$ 为 feasible solution
  • Optimal Solution: 取最值时对应的元素
  • Extremum: 最大值或最小值
  • Local Extremum: 在可行域与其邻域交集中能够取最值的元素 x
  • Objective Function: 目标函数，待最优化的对象
  • Constraints: 确定可行域的限制条件
  • Constrained optimization: $S \subseteq D$ Unconstrained OptimizationL $S = D$
  • Greedy Method: 贪心算法，每一步都选取局部最优解 ->对于优化问题每一步都考虑梯度方向

The Unconstrained Case

a6cb18f2e28ec5ddb52c04de56b4e8a.png

  • 对于局部极值，如果函数在该点存在偏导，则其梯度为 0
  • 注意：critical point 的梯度为 0，但并不意味着 cirtical point 即对应局部极值，注意经过此点对 contour 进行 parametrization 非 smooth
  • 注意:critical point 只能判断内点情况，对于开集需要单独考虑其边界情况或者考察函数于无穷处的极限情况（见 Homework10 T1 24)
  • 利用海塞矩阵的正定或负定情况判断 critical points 是否为局部极值

Quadratic Approximation for Multivariable Functions

9c9084b825d17977b78ff97c96068bc.png

  • 利用一阶微分，及其对应的 Jacobi Matrix 或者 Gradient 对函数进行线性近似
  • 利用二阶微分，考虑对函数进行二次近似（类比 Talyor)

0f3382581e3c49a9ce6b8535249b9ff.png

推论：利用正定情况与否确定 critical point 是否能对应局部极值

a74dd6470f9c8cfb133429230c064cc.png

注意选取的点需为 interior point,不能是 boundary point

n=2 的情况
76276169a882e42cee5712400da9fa0.png

核心依然为判断二阶的海塞矩阵是否正定,直接利用行列式判断，恒大于 0 既可以确定极值
区分 Local Maximum 与 Local Minimum->利用 A 的符号判断，即为利用二阶微分判断一阶的情况进而确定 Local Maximum 还是 Local Minimum

  • $A > 0$ Local Maximum
  • $A < 0$ Local Minimum

d7e6f20bcb87cbb928f08fc896cc960.png
对于海塞矩阵半正定的情况，我们无法直接判断 f 是否存在局部极值

Saddle Point: 鞍点 ->一阶微分为 0（critical point)，海塞矩阵行列式小于 0,合成后的两平方项符号相反 ->无局部极值

f0c5d4262b3e0cdd5f079b306066b68.png
注意，对于非满秩的情况，海塞矩阵不能用来判断 saddle point,此时 $AC-B^{2}=0$

Example

[!tip] 思路总结

  • 对于 interior point,直接利用以上理论 (critical point,海塞矩阵正定等) 进行相关判断
  • 对于 boundary point,考虑分别固定对应变量，考虑唯一变量的变化（即确定函数值在边界上的变化
  • 对于定义域无界的情况，若要取到最值我们则需证明：在一个有界的区域内，函数可以取到最值；在无穷的部分函数无法取最值
  • 理论支撑：定义在非空紧集上的函数一定能在紧集中取到最大值与最小值

如何验证我们之前研究出的 Local Extrema 以及 boundary point 上的极值是否为 global extrema?->Theorem listed as below

理论支撑：

定义在非空紧集上的函数一定能在紧集中取到最大值与最小值
->
意味着当我们研究定义在无界区域内函数的最值时，我们需要证明无穷情况的取值小于或大于我们在有界区域内取到的最大值或最小值。同时还需关注函数的连续性

关注连续性、有界性、封闭性

30a836695d7b87945d79c07dee51ad0.png

从 $S$ 有界利用连续性与 Bolzano-Weierstrass 定理推及 $f(S)$ 的上下界

  • Bolzano-Weierstrass 定理
    $\mathbb{R}^{n}$ 中的有界无穷数列一定存在一个收敛的子数列
    04f17a9d660e74de5bb975a364b166b.png

  • 实数完备性定理
    7dd920f33a7b988f31f8c1f5b771c1b.png

6081aa70245ceee455c4533b4842f4f.png

078c2c0c138f4da5b314497fde00b18.png

关注 Problem 4

Optimization with Equality Constraints

问题描述：即在一系列等式的限制条件下实现最优化
a90db17faac4b535abe036d8bc4bc6e.png

  • Method1:
    利用非限制性的优化方法，通过换元方法表示限制条件后考虑求解 critical point
  • Method2:
    Theorem: Lagrange Multipliers 拉格朗日乘数法

3f9779ec9840ad0e116a5315f79f6aa.png

条件

  • $f$ , $g$ 一阶可微
  • 满足的 m 个限制条件构成的函数其 Jacobi Matrix 行满秩，考试时注意检验
  • f 在定义域内有局部极值 ->该点 gradient 可用 $g$ 的行进行线性表示

注意

  • 对于 $m=1$ 的特殊情况， 由 $f$ 与 $g$ 的 gradient 相互平行 -> $f$ 与 $g$ 在对应点共享一个切空间（在 smooth 的情况下，即 gradient 不为 0）
  • 在限制条件所对应的 Jacobi Matrix 不行满秩的情况下，不满足拉格朗日乘数法的条件，但是仍有可能存在局部极值
  • 拉格朗日乘数法需要 D 为开集，对于 $S\cap \partial D$ 上的点需要每个单独检验，不能利用拉格朗日乘数法
  • 当限制条件为给定的一个区域时 ->一方面考虑区域内的 critical point，另一方面在边界上利用拉格朗日乘数法，最后比较两部分分别求出来的极值

deeb9b5f95a655e1c6e0123478a9940.png
Proof: 整体思路为引入引理说明各曲线在 0 处对应点的 Tagent Vector 可构成限制于 Jacobi Matirx 的零空间，然后利用零空间的包含关系说明