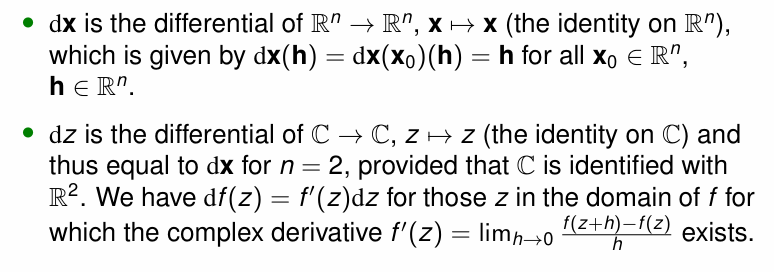#Math241

Differentiable Maps

Intuition of Differentiation

进行微分的核心目的即为利用线性映射对局部进行拟合估计
-> 追溯微分的定义式，我们可以考虑将函数在某点处附近增量表示为 原值 +Linear h+ Remainder 的形式

  • Remainder 余项可用 small-o notation 表示，核心即为需要满足：

limh→0R(h)h=0

Example

8bb8ccc26d7ea16b193dd18daa42f4e.png
4b7925cebb981b8d7356106e386906e.png

对于不能简单用多项式函数表示的情况 ->考虑直接展开成多项式形式
09bb9789066c902ee1b4c24a875d573.png

Concept

5fa4c8e5117d009afe37bf8083ed7d0.png

Notes

  • 可以用极限替代小 o 记号

d05b5dda956366fbfb962e78971d561.png

  • 线性映射是唯一的
    89d5297a1c6becf6b935f24db0eaf86.png

  • Jacobian Matrix->表示 h 不同维线性组合的系数
    dbd7872d817c1a26d589e52eec2e6db.png

  • Coordinate-wise Differentiation

More on Examples

  • Linear and Affine Maps
    43591db1fbfeebd53712ec5920e728c.png

  • Quadratic Forms

3debf8ae58aa8d0ba7c804511f0ab7d.png
2668d282854bfaf3e01380e987b8fe6.png

  • Length Function

6371dbcf527483ab323f0a5a83dc778.png
8f68782879bce308bc205949240079c.png

Partial Derivatives

Definition

偏导：考虑固定其余变量，考察函数关于某一特定变量的变化率
264b9e75e6773dbf162b21739b22235.png
3875b52f6e5ae8c7a9bc681b9c71a90.png

注意

  • 偏导函数的定义域 ->相对应的点对应的微分极限存在
  • Differentiability -> Partial Differentiability

3b0340ead8f92b1dfeea8fa160025fe.png

Theorem

5b4d63670778a60658bfe58ac1cb3b7.png

  • 注意雅可比矩阵的写法：每一行即为一个映射，每一列依次为对不同的变量求偏导
  • 靠近 x 偏导存在且偏导函数连续 ->f 在 x 处可导

f9f5a7d0dcd9ed61df0ed28171216eb.png

a58a83331568627afdddfe360f73321.png

Example

注意偏导在存在 (0，0) 存在取值，但是极限不存在 ->不连续

3370b6c8923baaa14f9d2923d6e5a6d.png

Further Concept

Directional Derivatives

Definition: 即从一个方向趋近函数求其微分
注意方向微分的基本定义，可以从基本定义出发判断该方向微分是否存在
例如 Worksheet 7
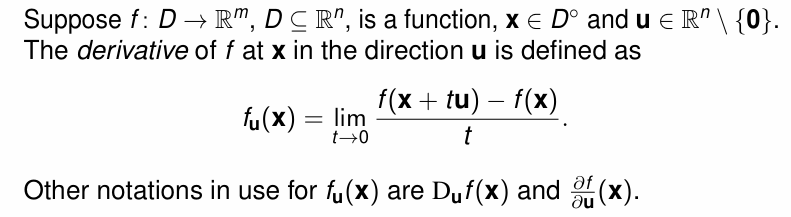
bc31e5b011ae27800f2843773efb232.png
Notes:

  • Functional Vector 的模常常会影响 Functional Derivatives,所以我们一般选取单位向量
  • 当 m=1（即映射结果只有 1 维时），如果选取的方向向量方向与 Jf(x) 相同或相反，我们可以得到 Gf 的最大值或最小值
    7da9d192230cfff3800017179301c3c.png

注意对于 Directional Derivative,我们有 fu(x)=df(x)(u)
或：

Duf=∇f⋅u

利用单位方向向量与梯度的点乘确定 Graph 在某个方向上的斜率

当方向向量与 Gradient Vector 同向时，其微分有最值（利用点乘关注两向量的夹角）

ec26f6e253e3493dce9783605efb86b.png

Jacobi Matrix矩阵的每一列表示了相对应变量在微分上的方向向量

Gradient

Definition
9301fd389f84a1308f03c0ea19694a7.png
gradient 即为函数关于所有 x 分量偏导的列向量,雅可比矩阵行向量的转置

Properties:

  • gradient 向量的方向即为函数值变化最快的方向,可以从 directional derivative 与 coutour map 角度考虑
  • gradient 向量的方向与 f 的等高线图垂直（注意可以利用 gradient 方向判断 contour 的切线方向） 直接考虑对 contour 两侧同时求偏导即可得到 Gradient 与 Contour 对应点的 Tangent Vector 正交

ab4bf8c8d4ea34d279de821548a227f.png
51ad3c5efee2f2c41440aba931f5d5b.png
注意 gradient vector 与 directional vector 的结合

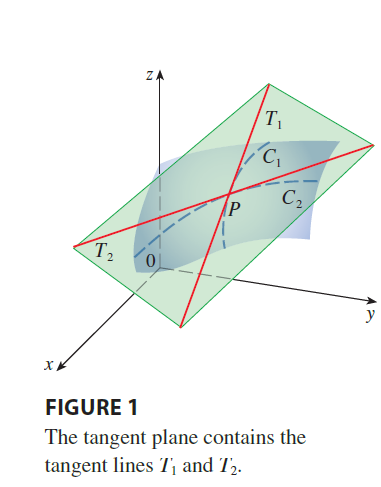
Tangent Space

核心即为利用微分实现对于函数的局部线性近似
f4a52087ec9a76b0b1509d8680c40db.png

Tangent Space 即为多元函数对应的自变量及其线性近似函数值向量拼接成的结果构成的线性空间
或者理解为对函数 f 的 Graph Gf 在给定点 (x0,y0) 附近的线性近似空间或者切空间，表示为函数 A 的 Graph

函数 A 即为对应的线性近似函数：

A:Rn→Rm.x→f(x0)+L(x−x0)

  • 可以用参数形式表示，写为对应点 + 线性近似的向量
  • 可以直接用方程形式表示（及类似与切线，仅需要将之前的斜率换成微分对应线性映射 A
  • 关注 m=1 的特殊情况
    2679eafad432e5711504b7380651e40.png

在三维空间中的直观定义：

19482dc0224aff841f7ddcafb0daaa2.png
9bb5c71c8d213749b31ab2d8b18af69.png

ba82f450fe5cea2bc918ea467c58acb.png

重点关注三维空间中的公式

通过引入参数化曲面定义 Tangent Space
a0fc1441560245c15db2efc506f0425.png

Smooth 定义: 当参数曲面对应的映射可微，且雅可比矩阵列满秩时，参数曲面光滑

进一步地，我们定义 Tangent Space
28d002c9fa69a679d719086e5acfd62.png
Tangent Space 即为利用微分对多维函数在局部进行线性近似，此时 T 为 Rn 中一个 k 维仿射子空间（在雅可比矩阵列满秩时）

g(x0) 即为多维函数的局部待近似点（或者为仿射空间的偏移向量）， Jg(x0)h 即为对应的线性近似空间

The Meaning of Differentials

2d8288b1e0289c5da8f19fb8ad97a5b.png
c8288ff257992d89e87fe0922713c99.png

  • dx即为恒等映射函数的微分
  • **dxj 即为函数 Rn→R,x→xj 的微分
  • dz 一样考虑对于复数的恒等映射

The Multivariable Chain Rule

Theorem:
6a61dfc78718ca6a47a504eec22b7f1.png
证明：
核心即为利用每一步可微带来的线性表示形成最终的复合表示，在证明过程中需要验证的即为是否满足线性
d4b7f0ca0ca3b619d1434a18740b057.png
b5e9b66271171bfb3f15d7ff6232be8.png
验证后面均为关于 h 的小项
73ff886cf86ef8ef735b36760542b1a.png

推论 1（考虑 Matirx Form 形式的 Chain Rule)

用矩阵形式表示微分的线性算子
ab6e328354e12b7be7a0bd89c92127c.png

Remark:
即对于一个多元函数经过多步映射得到的最终结果，如果我们需要考察最终结果关于初始变量的偏导，则需考虑整个复合映射过程所涉及到的所有中间变量，通过 Chain Rule 逐级向前得到最终结果

推论 2 (考虑梯度与 contour 切线向量的垂直关系)

541c8c7d218af94f9775cbbdb7b0167.png
注意：

  • Smooth Parametrization 即意味可以找到参数对 f 中的 x 进行参数化，且同时新实现的映射可微
  • 进行参数化是为构造一个曲线，使得可以关注曲线上的切线以及对应映射后结果梯度的关系
  • 对于映射到 n 维的情况，当我们考虑 n 维变量的 Level Surface 时（相当于对其加上一个限制条件）,在对应的 f 为 C1 function(偏导存在且在定义域上连续) 且其 gradient 不为 0，我们即可找到对应 n−1 维的参数化曲面，在此情况下函数 f 在点 x0 的梯度正交于参数化曲线 S 在该点的切空间
    g:Rn−1→Rn
    e9227801d81edf21d3fc3b6a0f258bd.png

考虑更具体的情况，如果需要求解对应参数化曲面的 Tangent Plane，只需要考虑：

∇f(x0)⋅(x−x0)=0

或者利用之前对于对应参数化曲面 Tangent Plane 的求法：

Tangent Plane: x0+R Columns of Jacobi matrix of g

Example 9778d98e04fa67985fa6d1e510708e4.png

推论 3 Inverse Function Theorem

前置条件: C1 Curve + 对应的雅可比矩阵列满秩
结论：可以在限制的定义域范围内找到函数 f 的逆 C1 curve
13059e83904b8c0999c6679f83124e7.png