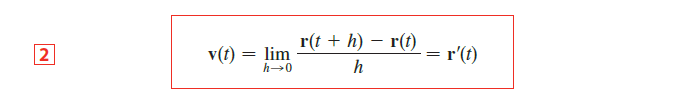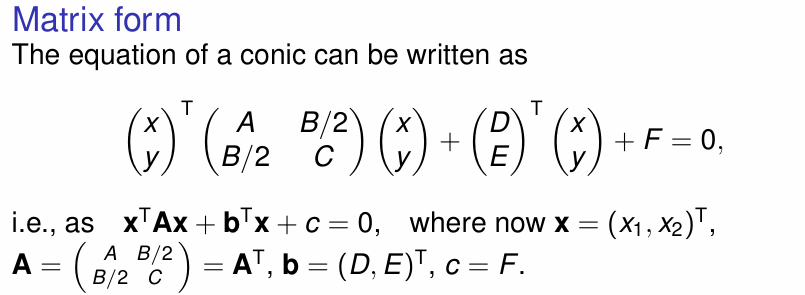Applications to Physics
#Math241
Coordinate Systems
Setup
通过 Linear Mapping 换系:一个正交矩阵用来替换正交基,一个平移向量确定原点

正交矩阵的基本性质
- 模长不变
意味该变换能够保持距离不变
Motion in Space: Velocity and Acceleration
Velocity, Speed and Acceleration
注意速度、速率与加速度取决于对曲线参数的选取,而曲率、曲线长度、转矩则独立于曲线参数的选取
- Acceleration
Tangential and Normal Components of Acceleration
其中: 可以分别利用点乘计算相应的系数(对于 T,N 的便捷计算则可以参考先后求一二阶导后考虑正交化)
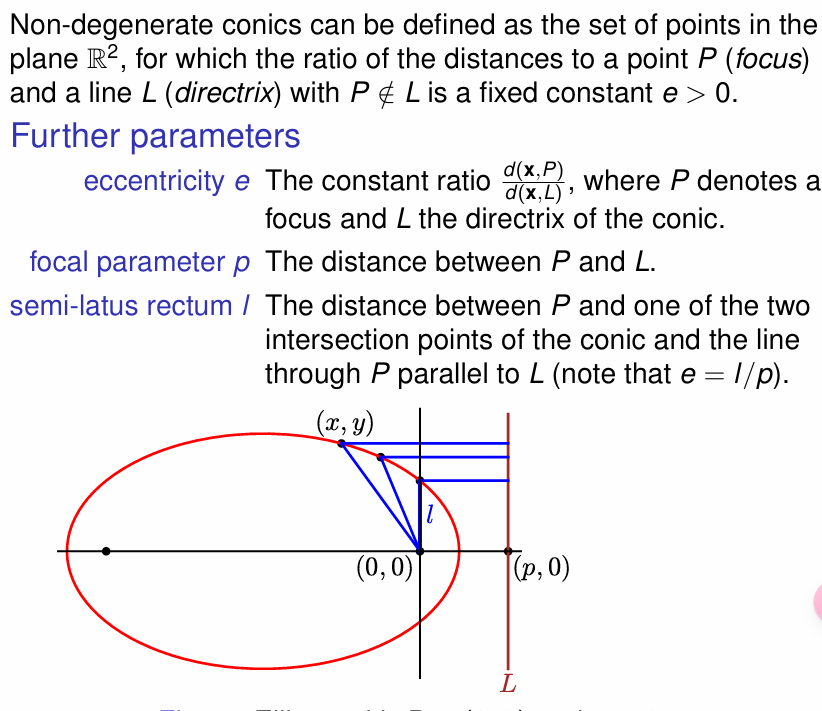
Polar form of Conics(圆锥曲线的极坐标形式)
Kepler’s Laws of Planetary Motion 开普勒行星运动定律
注意 e 与 l 的取值