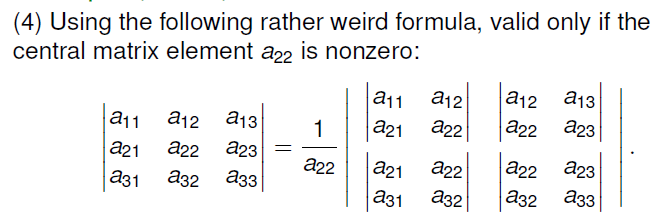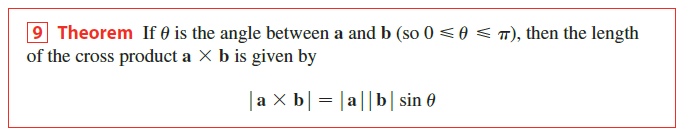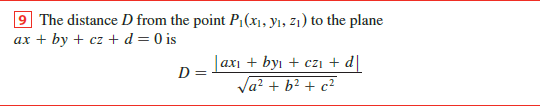Vector

#Math241

Length and Cross Product

Definition and Property

• Bilinear Form(Symmetric)
• Positive Definite
• Associative Law
• Distributive Law

Orthogonality 正交

Length

Cauchy-Schwarz Inequality

• 向量形式

$$a,b\in {\mathbb{R}}^n,|a\cdot b|\le |a||b|$$

• 展开式

$$ (a_{1}b_{1}+\dots a_{n}b_{n})^{2} \leq (a_{1}^{2}+\dots+a^{2}{n})(b{1}^{2}+\dots+b_{n}^{2}) $$

• 导出三角不等式

$$d(a,b)\le d(a,c)+d(c,b)$$

• 复数形式
  
• 证明：
  1. 判别式法：引入一个二次函数即可
  2. 直接利用 Lagrange 恒等式即可
     

$$|a{|}^2|b{|}^2-(a\cdot b{)}^2=|a\times b{|}^2$$

Determinant

Permutation

Property

详见线代

Geometric Property

Cross Product

在空间 ${\mathbb{R}}^n$ 中，我们可以定义 n-1 个向量的叉乘，这些向量叉乘的结果为一个垂直于这 (n-1) 个向量的向量
三维向量的叉乘：

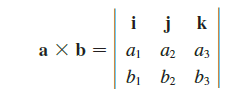
Property

特别注意性质 5、6

• 5 可以利用混合积的计算意义 ->体积理解 $det(a,b,c)=(a\times b)\cdot c$
• 6 考虑记住 triple cross product

Triple Product

$$a\cdot (b\times c)=\left|\begin{array}{c}{a}_1{a}_2{a}_3{b}_1{b}_2{b}_3{c}_1{c}_2{c}_3\end{array}\right|$$

几何意义：由向量 a,b,c 扩展出的平行六面体的体积,为三边向量张出的四面体的六倍
$V=|a\cdot (b\times c)|$
推论: 当 V=0 时，说明向量 a,b,c 共面（行列式为 0，线性相关）
Vector Triple Product:
$a\times (b\times c)$

平行六面体：parallelepiped
棱锥体：pyramid($\frac{1}{6}$ 的混合积)

常用计算

基本转换

• Line:

$$\begin{array}{rlr}& a+\mathbb{R}b⟺\left[\begin{array}{c}{x}_0{y}_0{z}_0\end{array}\right]+t\left[\begin{array}{c}abc\end{array}\right]\text{ 点加方向向量}& \frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}\text{ symmetric form}\end{array}$$

由两个平面求交线得到：

1. 直接求对应线性方程组的通解
2. 考虑对两平面法向量做叉乘也可

• Plane:
  方程形式

$$a(x-x_0)+b(y-y_0)+c(z-z_0)=0$$

其中：

$$\begin{array}{rlr}& \left[\begin{array}{c}abc\end{array}\right]\text{即为平面的法向量}& \left[\begin{array}{c}{x}_0{y}_0{z}_0\end{array}\right]\text{即为平面偏离原点的距离}\end{array}$$

参数形式：

$$\begin{array}{r}a+\mathbb{R}b+\mathbb{R}c\text{点+两个方向向量}\end{array}$$

向量形式：

$$n\cdot r=n\cdot r_0$$

具体计算

• 点与直线的距离
  确定点与直线上一点的向量，然后考虑其向直线的方向向量做投影

$$d(P,l)=\overrightarrow{b}-\frac{\overrightarrow{b}\cdot \overrightarrow{a}}{|a{|}^2}\overrightarrow{a}$$

• 点与平面的距离
  确定点与平面上一点，考虑对平面的法向量做叉乘
  在 ${\mathbb{R}}^3$ 中，我们有以下结果:
  

• 直线与直线之间的距离
  注意一面直线既不平行也不相交
  表示形式:

$$l_1:a_1+\mathbb{R}{b}_1\text{ , }{l}_2:a_2+\mathbb{R}{b}_2$$

考虑直线之间的距离即为考虑直线对应向量的最小值,即可转化为求点到平面的距离：

$$d(l_1,l_2)=min(a_1-a_2-({\lambda }_1{b}_1+{\lambda }_2{b}_2))$$

• 平面与平面之间的距离
  转化为平面与点之间的距离或