#Math241

建立平面坐标系

  • 固定的参考点（原点）
  • 坐标轴的方向向量
  • 单位长度

直线

  1. 确定直线的方向
    • 直线上一点 + 方向向量
    • 直线上两点
      不同的表示形式：

$$ \begin{align} & l = p + \mathbb{R}q
& l = (1- \lambda)p + \lambda q \end{align} $$

  1. 基本相关
    • 确定直线的交角 ->考虑点乘
      对于任意两直线的方向向量:$p, q$,我们有：

$$ \begin{align}
& \cos(\phi) = \frac{p \cdot q}{|p||q|}
& p \cdot q > 0 \ \text{两直线夹角为锐角}
& p \cdot q = 0 \ \text{两直线夹角为直角}
& p \cdot q < 0 \ \text{两直线夹角为钝角}
\end{align} $$

  • 确定两向量确定平行四边形的面积
    ec01aaaeca9219c6ffb9153d2072d12.png
  • 确定两向量之间的投影
    $(b-\lambda a)\cdot a=0$
    dd4b60c28db6252abaf909467d5720c.png
  • 换系：
    将新的坐标轴方向向量用原轴方向向量表示（Linear combination)
    同时注意如果有平移再加上一个向量确定移动后的原点
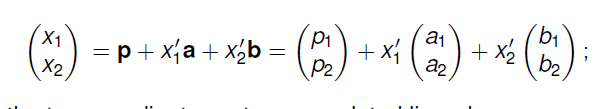
    09b85107e2df380a6dc03c4572611cb.png

三维坐标系

距离计算

  • 两直线之间的距离 ->本质上即为一点到一平面的距离（直接利用线代计算投影）
    或者理解为寻找两直线公共的法向量
    或者考虑向平面的法向量做投影
    78999cf617cfbecd658fb6bb1dc0694.png

从不同的视角理解向量

  • 考虑向量作为笛卡尔积中的点
  • 将向量视作一个方向与模长都确定 arrow，可以进行向量的加法

$$ T: \mathbb{R}^{2}\to \mathbb{R}^{2}, x = \begin{bmatrix} x_{1}
x_{2} \end{bmatrix} \to x+v = \begin{bmatrix} x_{1}+v_{1}
x_{2} + v_{2} \end{bmatrix} $$

Combination

Linear Combination

对向量集做任意的线性组合（Scalar+Addition)
线性子空间需要满足的条件 (也是验证一个线性空间的基本方式）：

  • 包含元素 0
  • 取集合中的任意两个元素
  • 对任意向量倍乘仍在该集合内
    3d736a7ba7082fb2aaea54138a81267.png
    a312ec9ce6f6413767a3f0c7d813789.png

Affine Combination

ef6f41b90319269fa54d89155f67084.png
上述性质等价的证明：
e76552e90e0086be71a2b7d5440d541.png
665b949533b7bc96b8078d37b426685.png

87c377d94b794a1ae431e3e06e2a196.png

  • 与线段定比分点的联系
    970797bc7a43945571a60319e677c62.png

凸组合与凸集

当仿射组合的系数均为正时我们组成了一个凸组合
44c0b85628be3a01700651181702086.png

Equational and Parametric Representation

Equational Representation

将线性空间表现为线性方程组解的集合
在 $\mathbb{R}^{3}$ 中，直线、平面以及点的表示形式分别为：

$$ \begin{align} & a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}=b \ ((a_{1},a_{2},a_{3})\in \mathbb{R}^{3} \setminus {0})
& a_{1}(x_{1}-p_{1})+a_{2}(x_{2}-p_{2})+a_{3}(x_{3}-p_{3})=0 \ \text{空间中确定的点+法向量}
& \text{Line: The Intersection of two planes.}
& \text{Point: The Intersection of three planes.} \end{align} $$

方程表示与参数表示的转换：

  • 参数表示 ->方程表示
    1. 将参数表示代入方程考虑恒成立
    2. 直接代入特殊点以及利用自由度赋值求解
    3. 将平面分为点 + 法向量（利用垂直求解法向量）
  • 方程表示 ->参数表示
    直接考虑线性方程组的求解即可

Parametric Equation

  • Line

$$ r = r_{0} + \mathbb{R}v $$

ed23cf0b537965dd74b5d5a760f109e.png
Another Form of Representation: Symmetric Representation
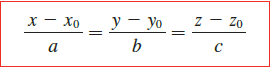
870a547c0e4fa6d5495d52cc1f3f6d4.png
ad2166b5bab66265d0b2d84aa07d8d9.png

  • Plane
    Vector Equation

$$ n \cdot (r-r_{0}) = 0 \text{ or } n \cdot r = n \cdot r_{0}
$$

Scalar Equation
f2f7e81e2c26d9ec2678e500c46bd36.png

Linear Equation

$$ ax+by+cz+d = 0 $$

  • Distance
    点到平面的距离
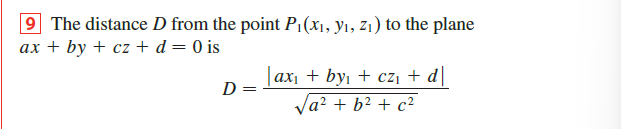
    36b16d64c880fd8354baa3269e7175e.png

  • 旋转与对称矩阵

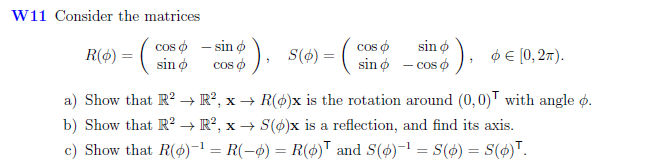
09f0218c9e8907685a3eacacaf9bc83.png

Cylinders and Quadratic Surfaces

Cylinders

Definition:
A cylinder is a surface that consists of all lines (called rulings) that are parallel to a
given line and pass through a given plane curve.

Quadric Surfaces(二次曲面)

Definition:
A quadric surface is the graph of a second-degree equation in three variables x, y, and
z. The most general such equation is
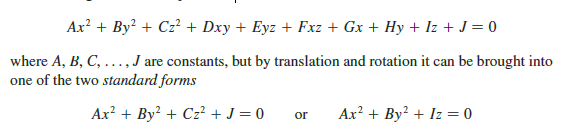
5707c2ee77d80522d80d3563bc88485.png

二次型相关汇总：(Homework4)
3e9b862570ecec1b3324f49c76e5882.png

  • 第一步利用

$$ \begin{bmatrix} A, B
B, C \end{bmatrix}\begin{bmatrix} x
y \end{bmatrix} = \begin{bmatrix} -D
-E \end{bmatrix} $$

判断该二次型是否中心对称，如果为中心对称，则可利用上述方程解出的唯一解将该二次曲线移回原点（非中心对称有多解）

  • 第二步考虑对一个非退化的二次曲线，利用一个旋转矩阵将交叉项消去，旋转矩阵系数由如下得到（具体的话考虑如何选取合适的参数使得交叉项系数为 0）

$$ \begin{bmatrix} x
y \end{bmatrix} = \begin{bmatrix} \cos\phi, -\sin \phi
\sin \phi, \cos \phi \end{bmatrix} \begin{bmatrix} x’
y’ \end{bmatrix} $$

最终化简为：

$$ \begin{align} & \lambda_{1}x’^{2} + \lambda_{2}y’^{2} + \frac{\Delta}{AC-B^{2}} = 0
& \lambda ^{2} -(A+C)\lambda +AC-B^{2}=0 \end{align} $$