Relations & Graphs
#Math213
Relation
Basic
定义:
给定两个非空集合 $A$ 和 $B$ ,它们的笛卡尔积 $A\times B$ 是所有有序对 $(a,b)$ 的集合,其中
$a\in A,b\in B$.
$$ A \times B= {(a,b)|a\in A,b\in B} $$
一个Relation $R$ 是笛卡尔积 $A \times B$ 的子集: $R \subseteq A \times B$
Binary Relation
Definition

Binary Relation 定义在两个集合之间,Relation 可以定义在多个集合之间
Relation on the set
Definition:
定义在集合 A 上的 relation 即为从集合 A 到其本身的 relation
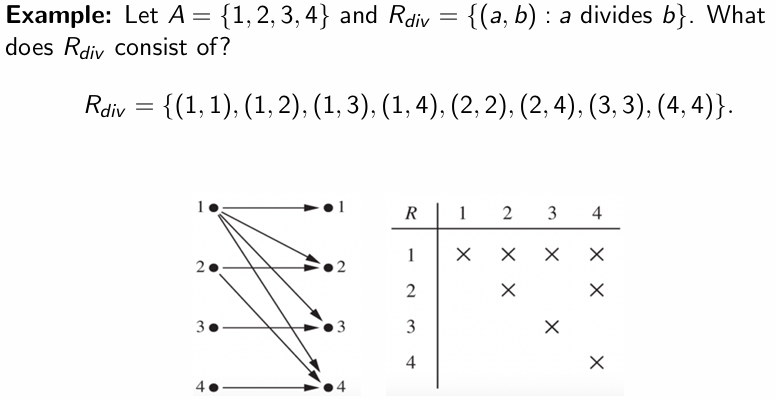
Number of Binary Relations
先分析笛卡尔积的势,再考虑其所有子集的数量

Representation
-
Use Arrows
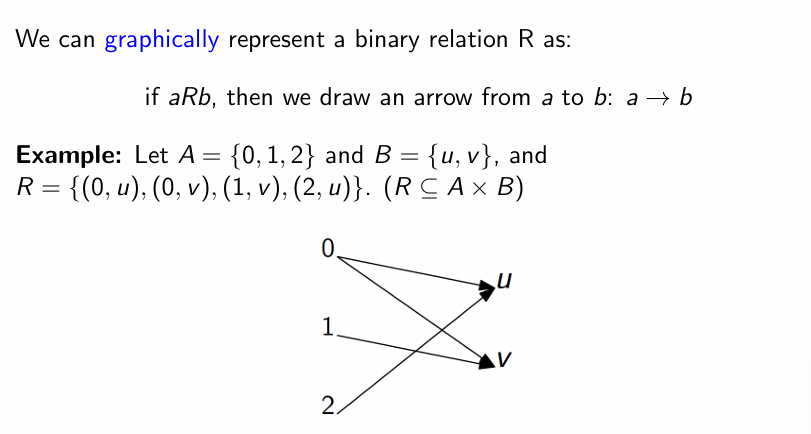
-
Use Table

-
Zero-One Matrix ->Represent Binart Relation
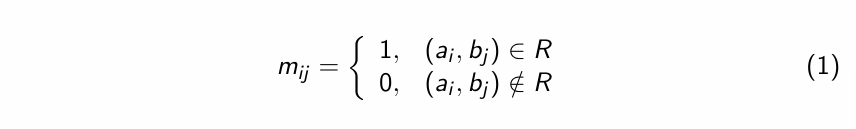

Join and Meet
Join—取并集,有 1 记为 1
Meet—取交集,全 1 记为 1
Composite of Relations
Boolean Product 直接用矩阵乘法理解即可
利用 Boolean Product 可以直接得到两个 Relation 的复合
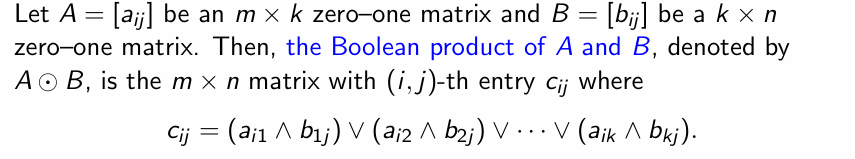
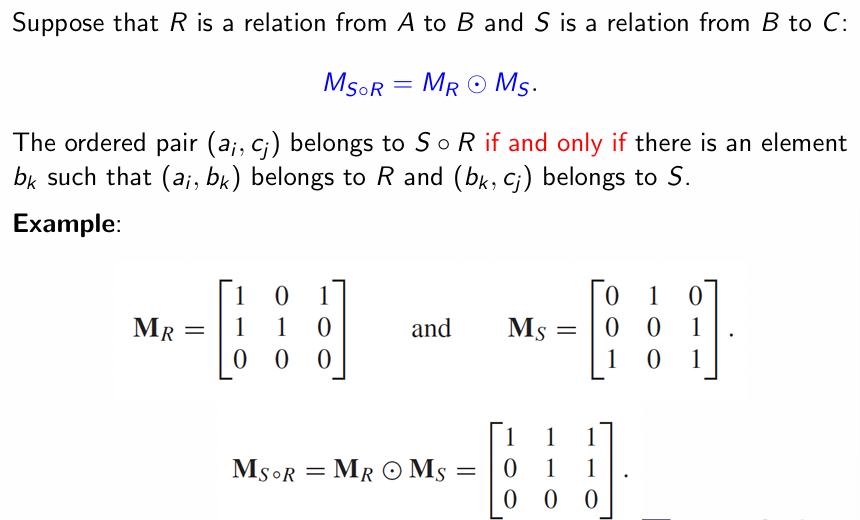
Properties of Relations
Reflexive Relation
对于集合 A 的任意一个元素 a,均有 $(a,a)\in R$ , R 为定义的 relation
从 Relation Matrix 上看即为其主对角线上的元素均为 1

Irreflexive Relation
对于集合 A 的任意一个元素 a,均有 $(a,a)\not\in R$ ,R 为定义的 Relation
注意 Irreflexive 与 Reflexive 并非互斥的关系,可以既不为 reflexive 也不为 irreflexive
Relation Matrix 的主对角线上均为 0

Symmetric Relation

对于任意的 $(a,b)\in R$ 均有 $(b,a)\in R$
表现在 Relation Matrix 上为 Relation Matrix 本身为对称
Antisymmetric Relation

除了对角线上元素,对于任意 $(a,b)\in R$ 均有 $(b,a)\not\in R$
Transitive Relation
传递性 Relation

Combining Relations
Relation 本身即为集合,因此可以对其利用集合的操作包括: union, intersection, difference 等等去组合不同的 relation
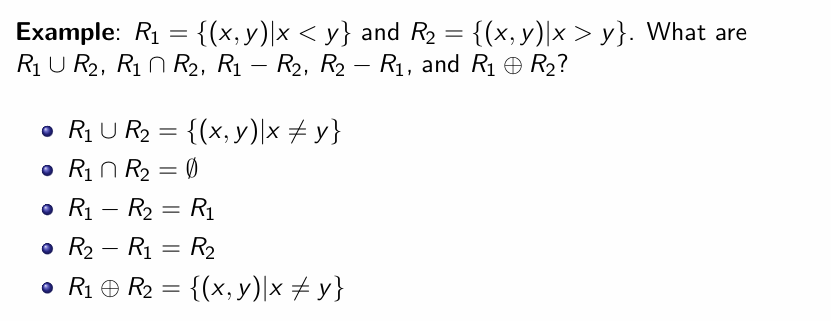
Composite of Relations
多个 Relation 的复合

注意复合的顺序 ->左手边的 Relation 作为复合映射的第二个映射
利用矩阵角度可以直接考虑经过矩阵乘法后的非零项
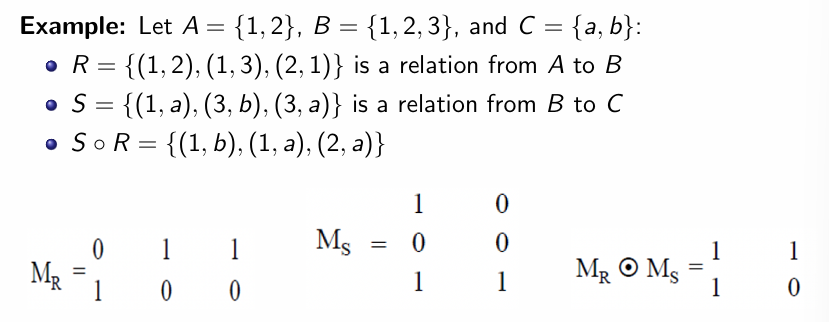
Power of a Relation
-
Definition
同一集合的多次复合

-
Transitive Relation and Power of a Relation

n-ary Relations
-
Definition
涉及多个集合 Cartesian Product 的子集

对于 Functional Domain, 其中任意一个元素均最多对应 Relation 中的一个 n 维元组
-
Relational Databases
关系数据库即为 n 元关系

Composite Key: 将不同的 domain 组合起来,其组合对应的 n 元组唯一

Operator
Selection Operator
根据满足某个特定条件对原有 Relation 进行筛选

Projection Operator
根据要求删减原有 Relation 的某些维度

Join Operator
将不同的 Relation 拼接形成新的 relation(将能够满足 transitive 进行拼接的拼接起来)

Closure of Relations
Definition

-
Reflexive Closure
R 的 Reflexive Closure 为满足通过增补元素使 R 满足 Reflexive 性质的最小 Relation

类似地,我们可以定义 reflexive closures, symmetric closures 与 transitive closures
-
Transitive Closure

Equivalence Relation 等价关系
1. 等价关系
[!tip] Definition
A relation R on a set A is called an Equivalence Relation when R is transitive, symmetric and reflexive.
同时满足传递性,对称型,自反性
Example
- 整数上的同余关系

2. 等价类
等价类包括给定元素在等价关系下相关的所有元素的集合

Theorem
在等价关系下,我们有以下关系等价
- $(a,b)\in R$
- $[a]=[b]$ 元素 a,b 等价类相等
- $[a]\cap[b]$ 非空集


3. 划分

给定集合可以被划分为一系列不交非空集合的并集
等价类与划分->我们可以按照等价类对集合进行划分

对于任意一个在集合上的划分,我们都可以将其中的集合作为其对应的等价类 ->当且仅当元素 $a,b$ 都属于同一个划分的子集时,我们有 $(a,b)\in R$
Partial Ordering & Total Ordering

偏序关系
Definition
偏序关系需要满足的性质
- 自反性
- 反对称性
- 传递性
我们可以将集合 $S$ 以及定义在其上的偏序关系 $R$ 一起叫做偏序集 (partially ordered set), 记为 $(S,R)$

Comparability 可比性
在偏序集中,当且仅当元素 a,b 之间有偏序关系才有可比性,否则元素 a,b 不可比

全序关系
全序集又称 totally ordered or linearly ordered set. 对应的关系称为 total order 与 linear order
对于全序集,其中的任意两个元素均具有可比性

Well-Ordered Set 良序集
良序集为特殊的全序集,需要满足以下条件
- 其对应的偏序关系为全序(集合 S 中任意元素均具有可比性)
- S 的任意一个非空子集均具有唯一最小元素

Lexicographic Ordering 字典序
给定两个有序集 $A_{1},A_{2}$,其字典序定义在其笛卡尔积 $A_{1}\times A_{2}$ 上,对于其笛卡尔积中的元素他们的比较关系通过如下确定:
- 优先比较第一个分量
- 如果第一个分量相等比较第二个分量

Hasse Diagram 哈斯图
Hasse Diagram 是一种图形表示法,用于直观显示偏序集中的元素及其偏序关系 ->Hasse Diagram 通过删除冗余的比较关系(包括自环、传递性)来简化偏序关系的表示
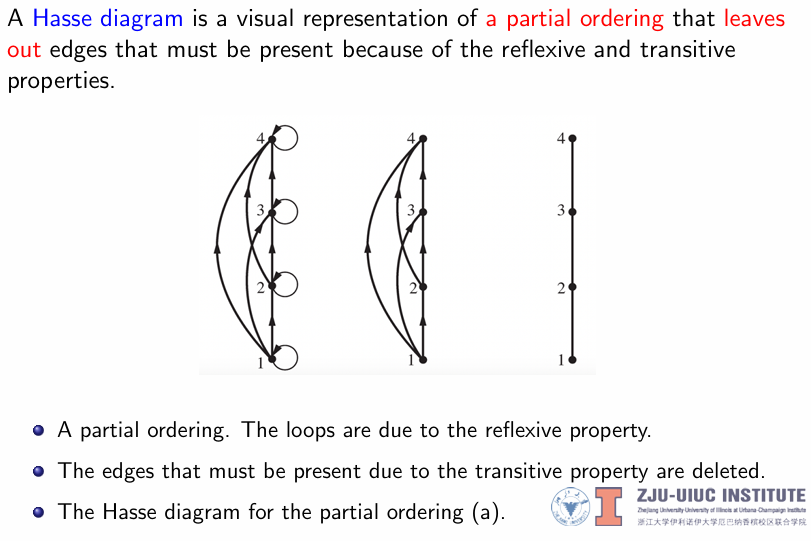
构造 Hasse Diagram 的过程
- 删除每一条自环边
- 删除传递性边 ->如果 $a\leq b,b\leq c$,则不直接连接 a,c
- 垂直排列:按照偏序关系的级别垂直排列,较小的元素位于下方,较大元素位于上方
Max(Min) & Greatest(Least) & bound
- Maximal and Minimal Elements
在偏序集中的 Maximal 或 Minimal 元素即为找不到其他元素与之具有 $\prec$ 或 $\succ$ 的元素

- Greatest and Least Element
Greatest 与 Least Elements 即为偏序关系中对任意其他元素都有 $\succ$ 或 $\prec$ 关系的元素

-
Upper and Lower bound

- **在偏序集中的 Maximal 或 Minimal 元素即为找不到其他元素与之具有 $\prec$ 或 $\succ$ 的元素
- Greatest 与 Least Elements 即为偏序关系中对任意其他元素都有 $\succ$ 或 $\prec$ 关系的元素
- 上界下界:与偏序集子集 A 中的任意元素均有偏序关系(大于/小于)
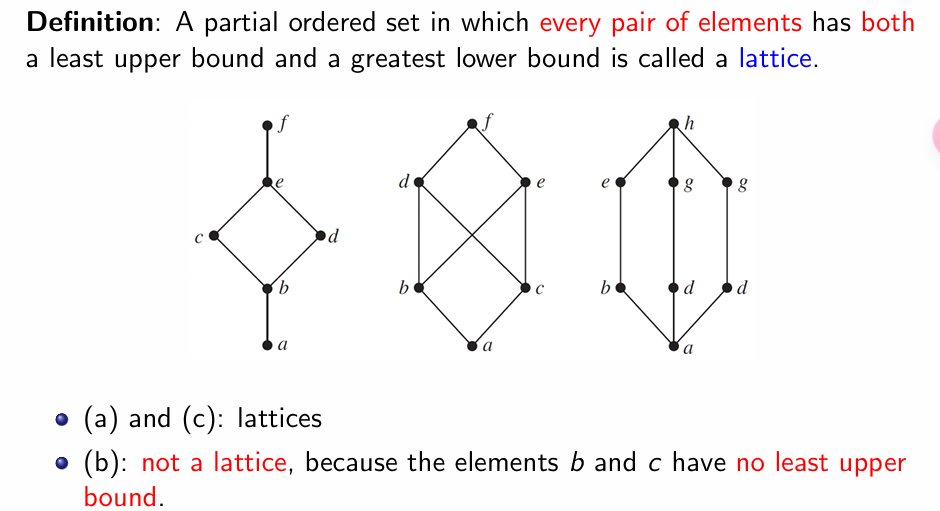
Lattices
注意偏序关系中的 Lattice 即为对于关系中任意一对元素均有最小上确界与最大下确界
Graph
Basic
1. Definition
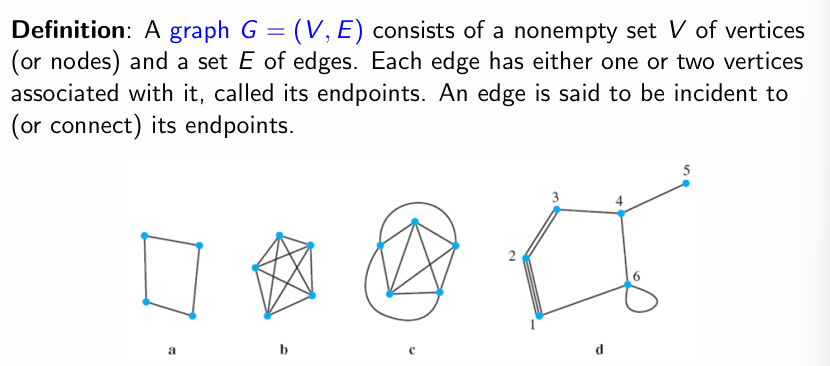
子图 Subgrph
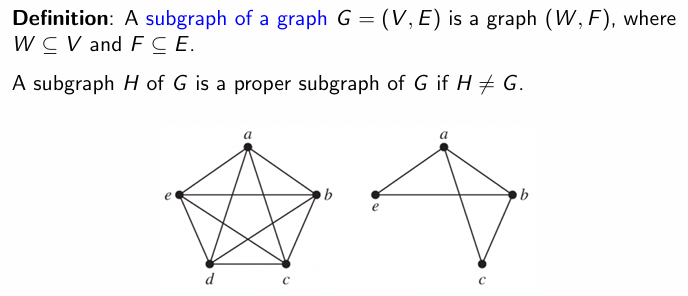
proper subgraph->非 Graph 本身的子图
图的并集
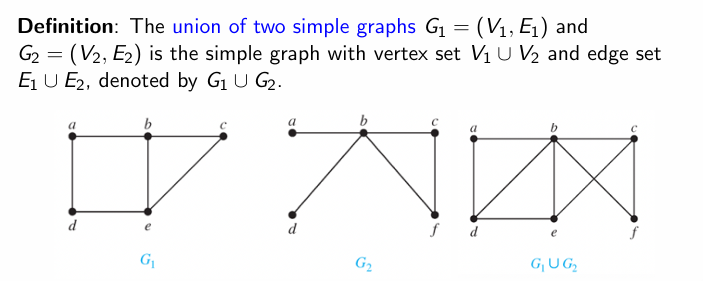
2. 简单分类
[!tip] 图的简单分类
- Simple graph, Multigraph, Pseudograph
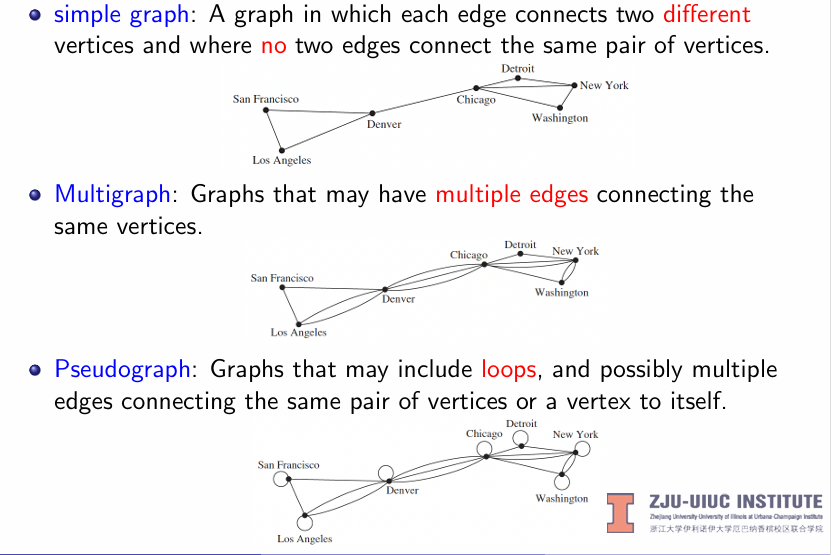
- Simple graph: 图中每一条边都连接不同的节点,且没有两条边连接同一对节点
- Multigraph: 图中存在多条边连接同一对节点
- Pseudograph: 图中可能存在自环或者多条边连接同一对节点或者节点与自己本身
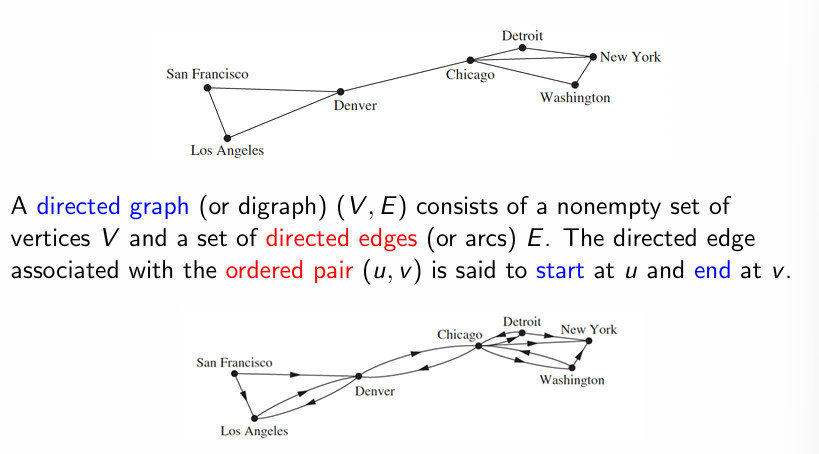
- Directed and Undirected Graph
- Directed Graph: 图中的边为有向边
- Undirected Graph: 图中的边为无向边
3. 特殊图
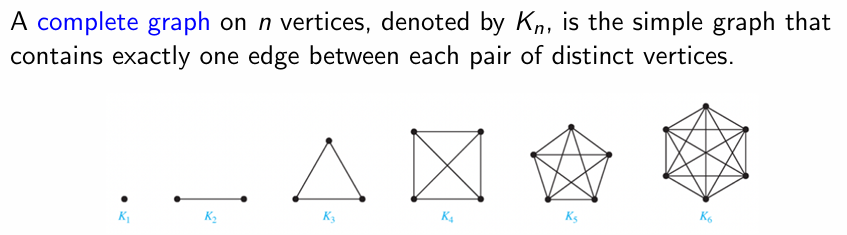
- 完全图:简单图中任意两个节点均有边相连
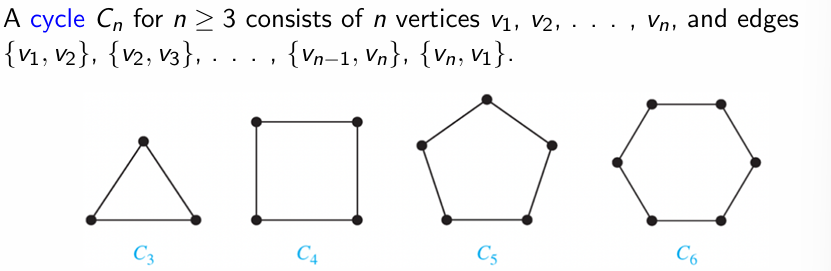
- Cycle: 节点依次相连形成环
-
Wheel: 在 Cycle 的基础上增加一个与所有点相连的的点
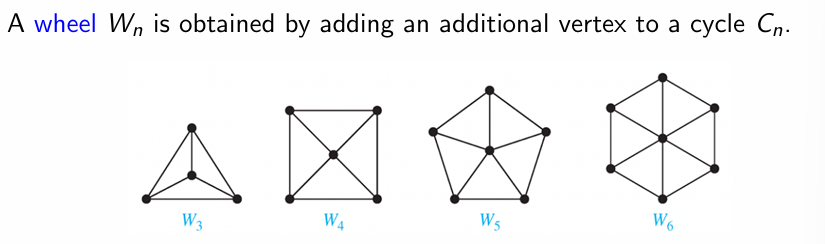
- N-dimensional Hypercube

Undirected Graph

- 相邻:无向图中存在边相连的节点
- 邻域:记无向图中与顶点 $v$ 相邻的的节点的集合记作它的邻域 $N(v)$
- 节点的度:无向图中节点的图即为与其相连的边的数量(注意需排除自环给节点贡献两条边的情况)
边与节点度的关系
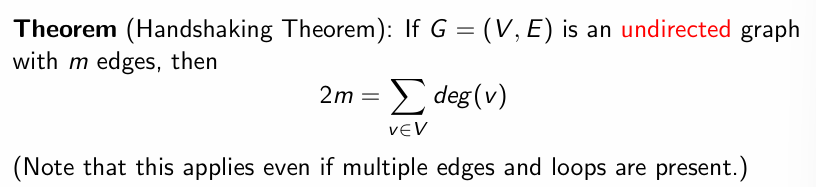
Directed Graph 有向图

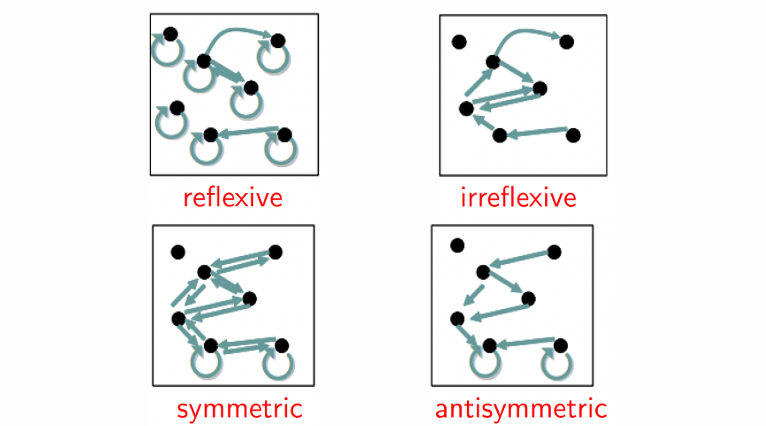
[!tip] Summary
Reflexive: 节点均有自环
Irreflexive: 节点均无自环
Symmetric: 边均为双向
Antisymmetric: 无双向边
-
节点的出度与入度

有向图中,出度和等于入度和
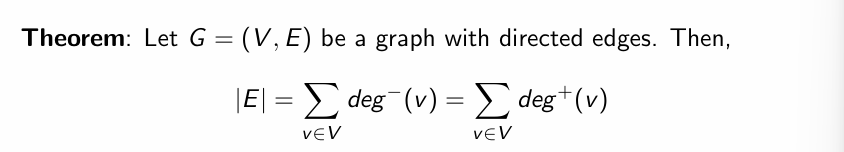
Paths in Directed Graphs
Definition
路:在有向图中从起点至终点沿着边的方向形成的路径
路的起点与终点相同 ->circuit/cycle(回路)

Theorem
从 $a$ 至 $b$ 长度为 n 的路存在当且仅当 $(a,b)\in \mathbb{R}^{n}$
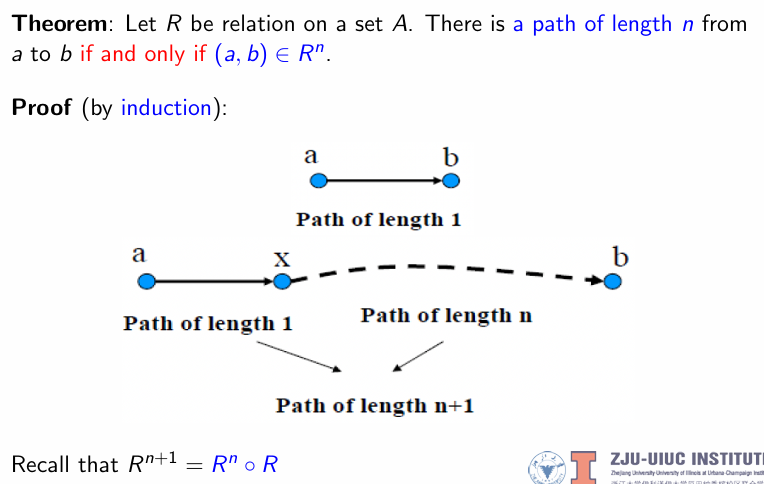
Connectivity


Theorem
传递闭包即为将有向图中所有能够通过路相连的节点均相连


进一步地,我们建立传递闭包与 0-1 矩阵的联系
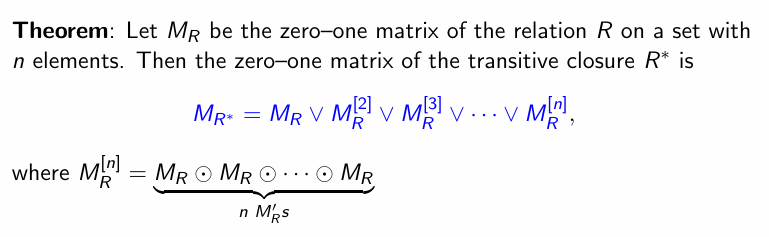
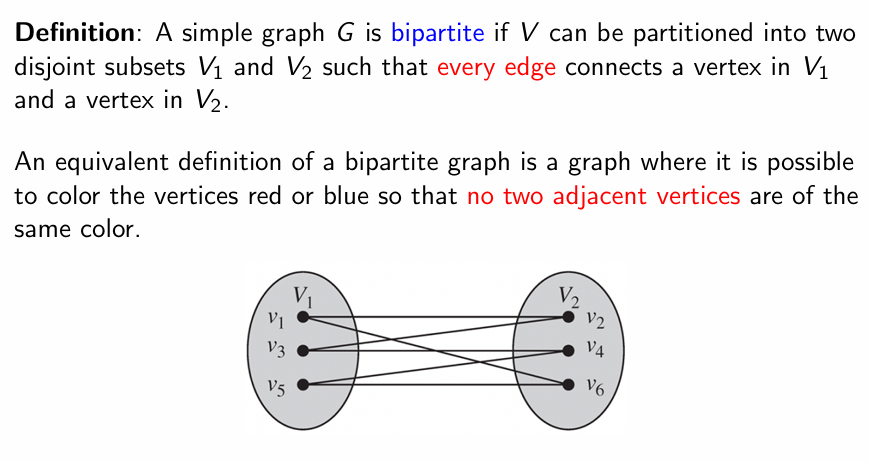
Bipartite Graphs
-
二部图:二部图中的任意一条边均连接图中存在的两不交分割的两个节点
-
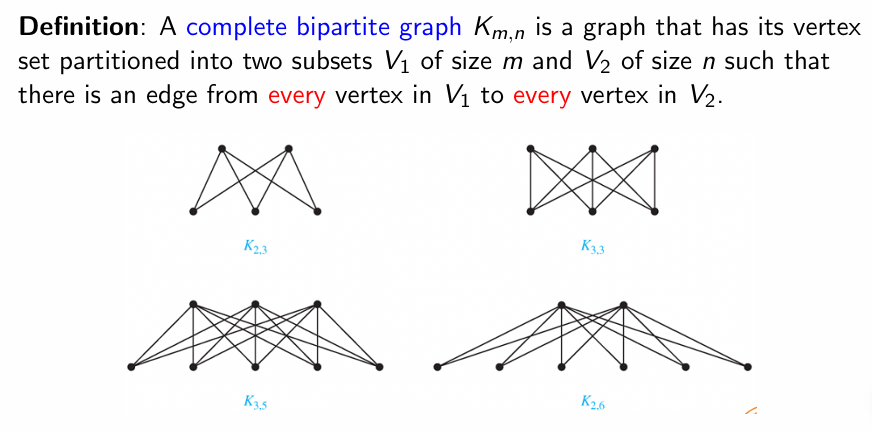
完全二部图:图 G 的分割 $V_{1},V_{2}$ 任意一对节点均有边相连
-
Bipartite Graphs and Matchings

Matching 为图中边的一个集合,其中没有两条边共享一个同一个顶点
**Maximum Matching and Complete Matching(最大匹配与完全匹配)

- 最大匹配:覆盖边数最多的匹配
- 完全匹配:从二部图的分割 $V_{1}$ 到 $V_{2}$ 的完全匹配为 $V_{1}$ 中的每一个顶点都在 M 中出现
- 完美匹配:将二部图中所有顶点两两配对,对于两个分割均为完全匹配
霍尔婚配定理

Representation of Graphs
- 邻接表(adjacency lists)

表示方法
- 如果图 $G$ 有 $n$ 个顶点 $V = {v_1, v_2, \dots, v_n}$,对于每个顶点 $v_i$,我们使用一个列表存储与 $v_i$ 相连的所有顶点。
- 对于无向图,若边 ${u, v}$ 存在,则在顶点 $u$ 的列表中包含 $u$ ,并在顶点 $v$ 的列表中包含 $u$ 。
- 对于有向图,若边 $(u,v)$ 存在,则在顶点 $u$ 的列表中包含 $v$
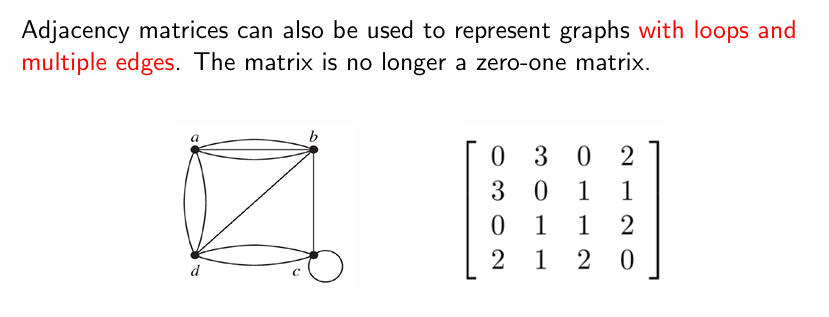
- 邻接矩阵(adjacency matrices)

用邻接矩阵表示图时,当图中存在自环或者一对节点有多边相连时,此时邻接矩阵非 0-1 矩阵
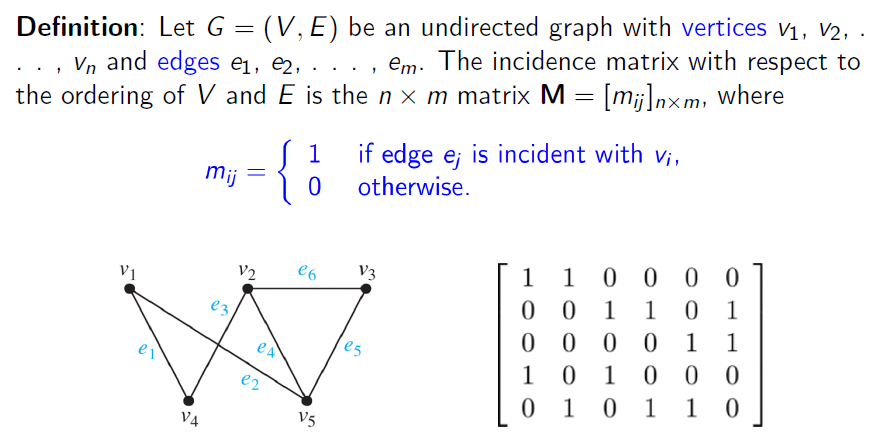
- 关联矩阵(incidence matrices)
关联矩阵按图中的节点顺序标记节点与图中每一条边的关系,若边与该节点相连,则在节点对应的列中标记为 1
Isomorphism of Graphs
同构图
Definition
两图同构当且仅当存在两顶点集间存在一个一一映射同时满足映射前后点的邻接关系,
此时这样的映射被称为Isomorphism.
核心思想为利用图的不变量:节点数、边数、度的情况来判断两图是否同构

判别
核心思想为利用图的不变量:节点数、边数、度的情况来判断两图是否同构
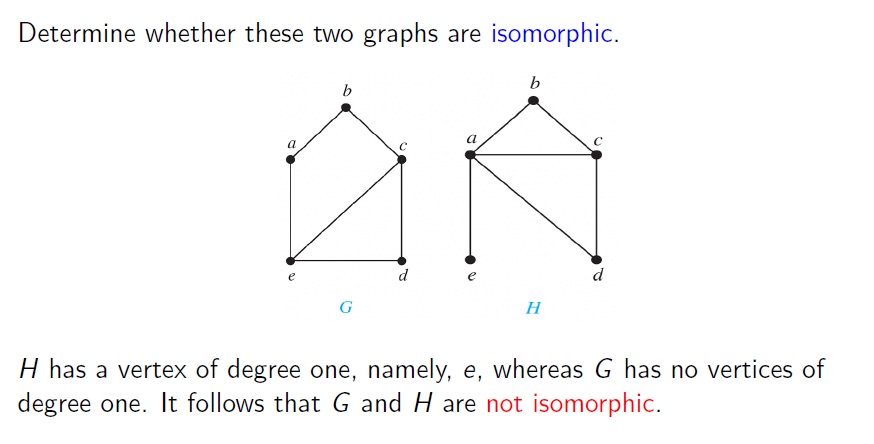
- Example1
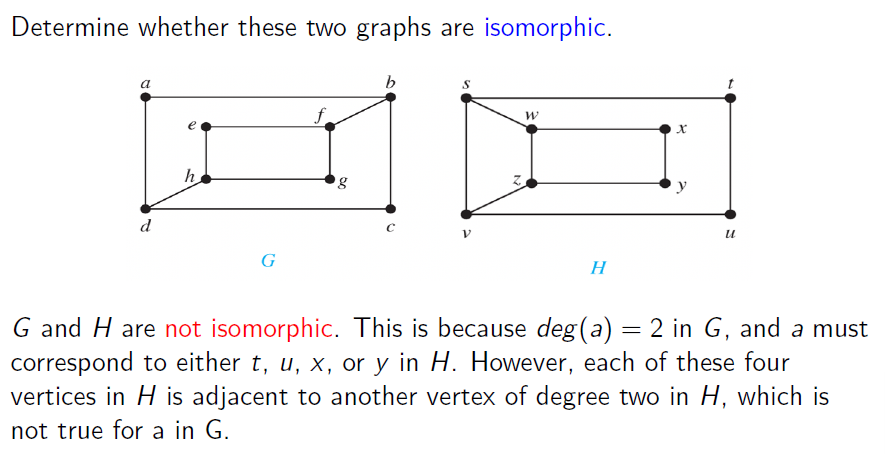
- Example2
- Example3:对于同构图直接构造同构映射

Path
1. 无向图中的路

- Circuit: 环路,路的起点与终点相同
- Simple path/circuit: 路中不存在重复边
- 路的长度:路中边的数量
连通性 Connectivity
- Connected Graph(连通图): 对于无向图,任意一对不同的节点之间均有路相连
- Disconnected Graph(非连通图): 对于无向图,存在不同的节点间没有路相连
- 性质:两节点间有路必有简单路(删去回路)-> 连通无向图间任意一对节点均有简单路
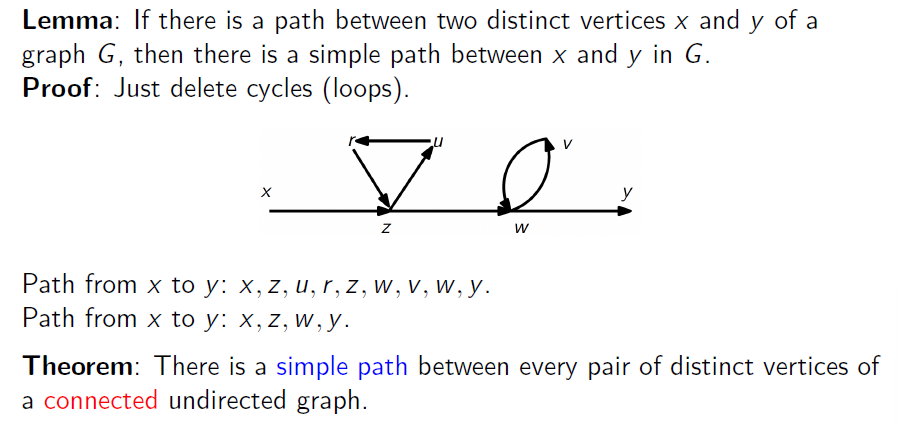
Connected Component: 连通分量
无向图中的连通分量,连通分量是一个子图,满足:
- 最大连通性:这个子图中的任意两个节点都通过路径连通,并且这个子图不能再加入其他顶点而保持连通
- 独立性:不同的连通分量之间没有共同的顶点或者边
当图中存在两个及以上连通分量时,该图不连通,此时图为其不交连通分量的并集

2. 有向图中的路

3. Cut Vertices and Cut Edges


- Cut Vertices: 在连通图中删去相应的节点以及与其相关的边,此时图不连通
- Cut Edges: 在连通图中删去该边,此时图不连通
- Edge Cut: 在图 G 中减去这些边的集合后,连通图变为非连通
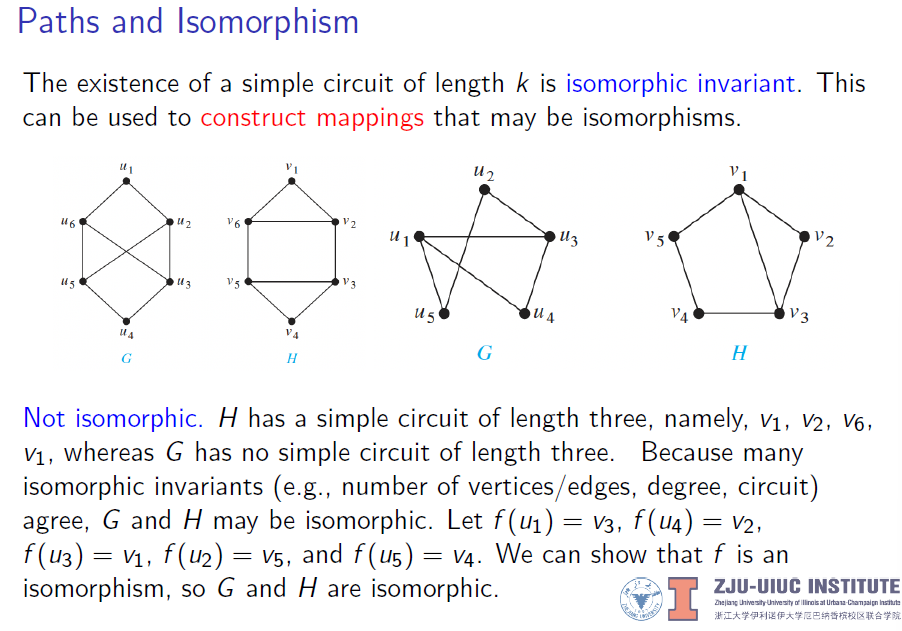
4. Paths and Isomorphism
利用路这一图形不变量来判断两图是否同构
5. Counting Paths between Vertices
在图 G 中,从点 $v_{i}$ 到 $v_{j}$ 路的条数即为 $A^{r}$ 中 $(i,j)$ 的项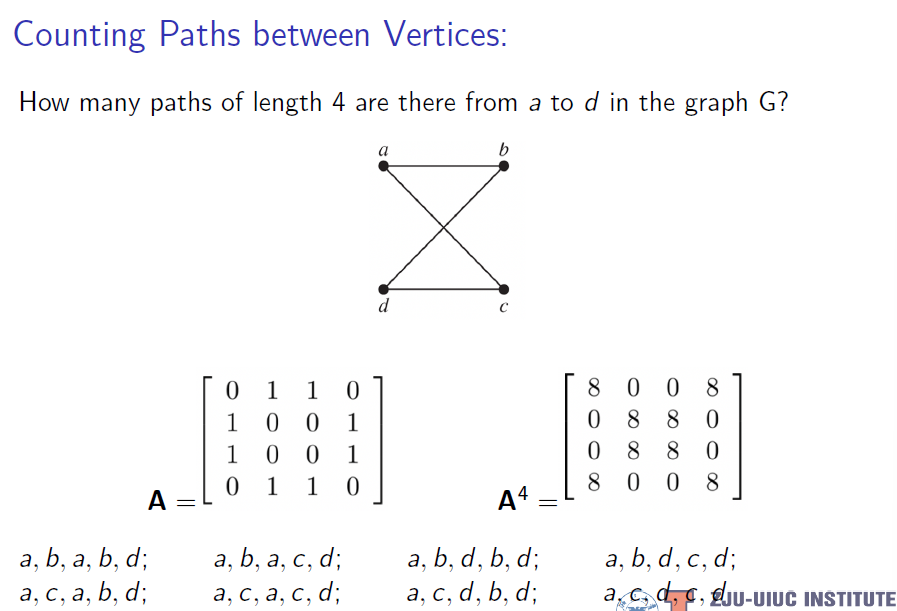
我们利用归纳法给出证明

6. Euler Paths and Circuits
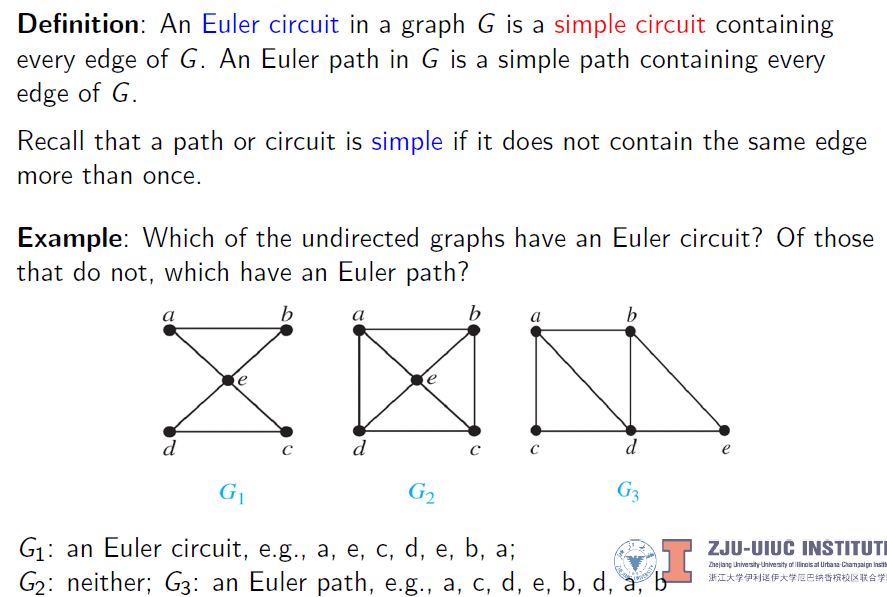
- Euler Path: 经过图中的每一条边且没有重复边(顶点允许重复)
- Euler Circuit:经过图中的每条边且经过一次的回路
基本性质
- Euler Circuit: 图中的每一个节点度数均为偶数 ->因为对于每一个节点必有出边与路边相对应
- Euler Path: 图中有且仅有两个节点度数为奇数(起点与终点)

当我们满足图中每个节点的度数均为偶数时,我们可以递归地构造一个 Euler Circuit

7. Hamilton Paths and Circuits
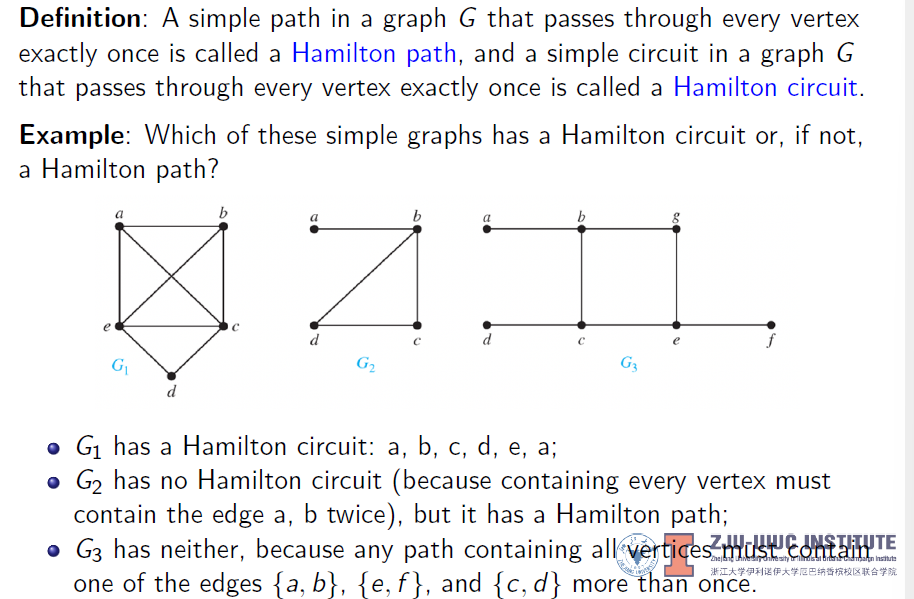
- Hamilton Paths 哈密顿路:经过图中每一个节点恰好一次的简单路
- Hamilton Circuit 哈密顿圈:经过图中每一个节点恰好一次的简单回路
若哈密顿圈存在,其路径内必然不能包括小圈 ->可以作为否定性的条件(分析圈的关系)
没有简单地判定哈密顿路或者圈的条件,但是我们有以下定理:
- Dirac’s Theorem: 若图 G 为简单图,且其中每个节点的度 $\geq \frac{n}{2}$ 则 G 存在哈密顿圈
-
Ore’s Theorem: 若图 G 为简单图,且对于图中任意一对非相邻的节点,均有 $deg(u)+deg(v)\geq n$,那么 G 存在哈密顿圈

最短路径问题 ->考虑 Dijkstra 算法
Planar Graphs
Definition
平面图:当图可以被绘制在二维平面上且满足没有边交叉时,我们称该图为平面图
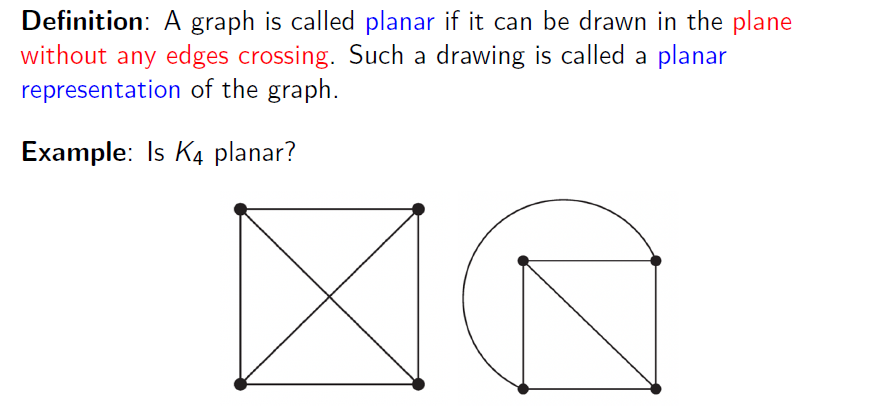
-
Euler’s Formula 欧拉公式
描述连通的简单平面图边数、顶点数与面数的关系
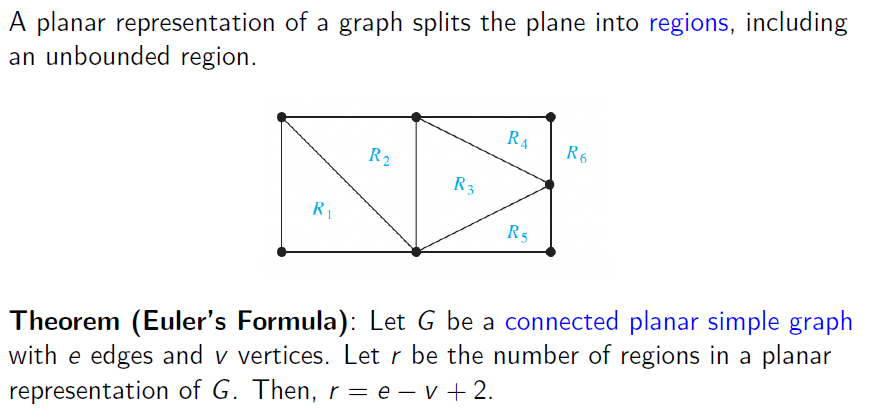

-
The Degree of Regions
区域的边数定义为区域边界上边的数目,当一条边在边界上出现两次时,它贡献两个度
对于平面图,我们有
$$ r=e-v+2 $$
-
推论
- 对于简单的连通平面图,有 $e\leq 3v-6$
- 对于简单的连通平面图,G 存在度数不大于 5 的节点
- 对于简单的连通平面图,若其中不存在长度为 3 的环路,那么我们有 $e\leq 2v-4$

利用边的总数与平面区域的度的关系构造不等式 ->一个区域的边界至少需要三条边

Graph Coloring
染色问题
简单图的着色问题(A coloring of a simple graph)
即为将颜色赋给图中的每一个节点,使得任意两个相邻的节点不会具有相同的颜色
Chromatic Number 色数
给一张图着色所需最小的颜色数目,记为 $\chi(G)$
四色定理
平面图的色数不超过 4
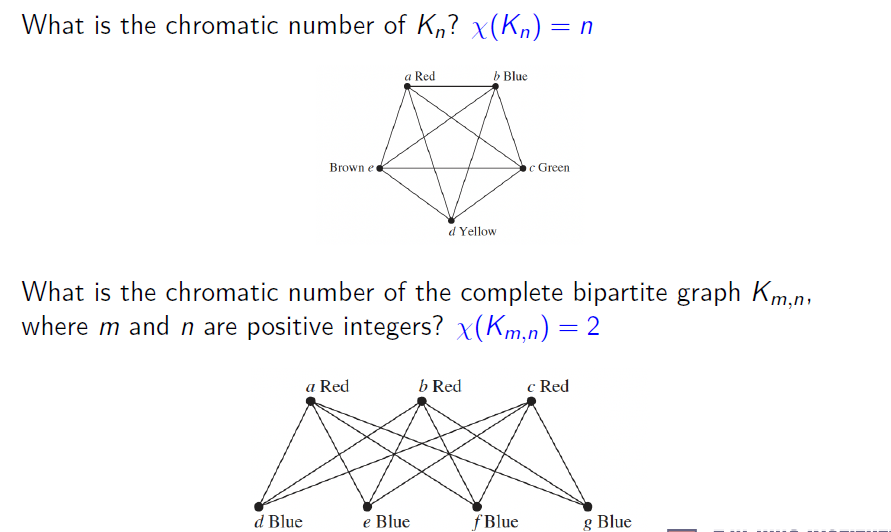
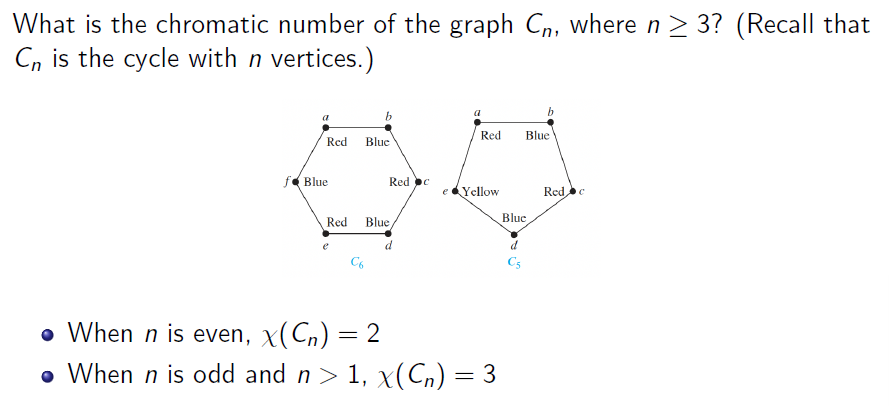
- n 阶完全图的色数一定为 n
- 完全二部图的色数均为 2
- 偶数个节点的圈色数为 2;奇数个节点的圈色数为 1
Tree
Basic
Definition
A tree is a connected undirected graph with no simple circuits.树即为没有简单回路的连通无向图
Theorem
An undirected graph is a tree iff there is a unique simple path between any two of its vertices.一个无向图是树当且仅当其任意两个节点之间都有一条唯一的简单路
Rooted Trees
Rooted tree 即为我们在一个 Unrooted tree 中选定一个根节点,然后将所有边方向记为远离这个根节点
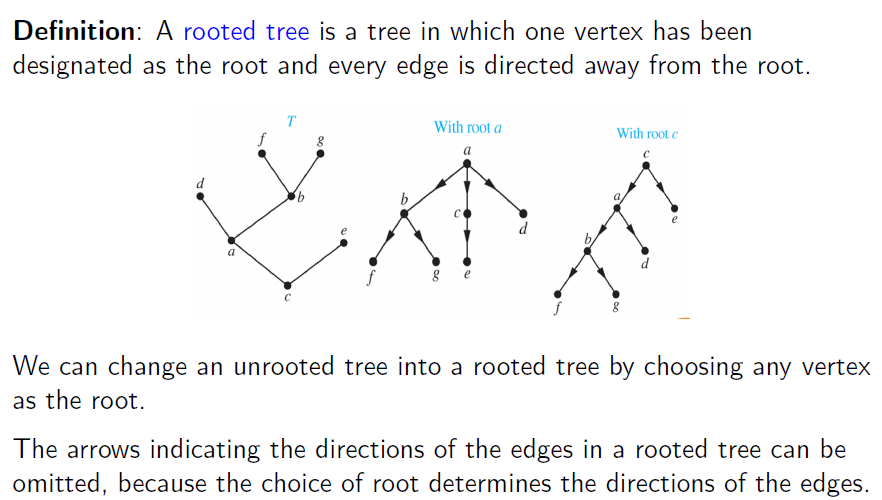

- Parent: 对于节点 $v$ 存在的唯一有有向边 $u\to v$ 的节点 $v$
- Child: u 为 v 的 parent, v 为 u 的 child
- Siblings: 具有相同 parent 的节点
- Ancestors: 从根节点到本节点路上的所有点
- Descendants: 所有以该节点作为 ancestors 的节点
- Leaf: 没有 child 的节点
- Internal Vertices: 有 child 的节点

每个节点的 Children 数量小于等于 m -> m-Ary tree
每个内点的 Children 数量均为 m -> full m-Ary tree


平衡树
对于高度为 h 的 m-ary 树,所有 Leaf node 的 Level 均为 h 或 h-1
Theorem: 高度为 h 的 m-ary 树中 leaf node 的个数

