#Math213

Counting

Basic

Basic Counting Rules

  • Product Rule：计数过程可以分解为一个彼此依赖序列计数过程，前项计数过程中的元素均与后项有关
    8056cf59d1afa612d4bdaeeb1d0a220.png

  • Sum Rule: 计数过程可以分解为一系列独立的计数过程
    b4678841d422202963d4b315af7b450.png

  • 容斥原理：Principle of Inclusion-Exclusion

$$ |\cup_{i=1}^{n}S_{i}| = \sum_{i}|S_{i}|-\sum_{i<j}|S_{i}\cap S_{j}|+\sum_{i<j<k}|S_{i}\cap S_{j}\cap S_{k}|+\dots+(-1)^{n-1}|S_{1}\cap\dots \cap S_{n}| $$

  • The Division Rule

4051e2d2ad04b1fd70e8129cebb7716.png

  • 抽屉原理： Pigeonhole Principle
    5dca018e09e39599ab4fadf88d6a92a.png
    泛化后的抽屉原理：
    6f37cd2339ab2bd96173906b919361a.png

Permutation and Combination

Permutation: 考虑不同对象的有序排列

$$ P(n,r) = n(n-1)\dots(n-r+1) = \frac{n!}{(n-r)!} $$

Combination: 考虑不同对象的选取

$$ C(n,r) = \frac{P(n,r)}{r!} = \frac{n!}{(n-r)!r!} $$

Combinatorial Proof

算两次
Definition

  • 利用计数原理考虑对同一计数事件从不同角度考虑，得出等式的两边
  • 利用构造双射证明等式两边相等 (核心为分别证明单射与满射)

17451c7a75156ed44c19db127293574.png
3221470c840ac1557eea0f7f4492296.png

Identity and Property

二项式定理

$$ (x+y)^{n}= \sum_{j=0}^{n}C_{n}^{j}x^{n-j}y^{j} = C_{n}^{0}x^{n} + \dots + C_{n}^{n}y^{n} $$

推论：

$$ \begin{align} & \sum_{k=0}^{n}C_{n}^{k} = 2^{n}
& \sum_{k=0}^{n}(-1)^{k}C_{n}^{k} = 0
& \sum_{k=0}^{n}2^{k}C_{n}^{k}=3^{n} \end{align} $$

Pascal’s Identity: 常用于组合数的裂项化简等

$$ C_{n+1}^{k} = C_{n}^{k} + C_{n}^{k-1} $$

推论：

$$ C_{n+1}^{r+1} = \sum_{j=r}^{n}C_{j}^{r} $$

三项式系数：Trinomial Coefficient

$$ \begin{pmatrix} n
k_{1} \ k_{2} \ k_{3} \end{pmatrix} = \frac{n!}{k_{1}!k_{2}!k_{3}!} $$

其中 $k_{1}+k_{2}+k_{3}=n$

Generalized Permutations and Combinations

Permutations with repetition

6b2aa6adc83815f6cd0a85ce546d556.png

Permutations with Indistinguishable Objects

49242ea8617d92d638b62005872e931.png

1f7880206a38f998bfc006cb5f59346.png

Combinations with Repetition

考虑将问题整体情境化归为带限制的不定方程，然后可以考虑隔板法

情境建模：

$$ a_{1} + \dots + a_{n} = k $$

其中 $a_{i}$ 为整数， $a_{i} \geq N_{i}$ ,则问题可以简化为：

$$ \begin{align} & (a_{1}-N_{1}+1) + \dots + (a_{n}-N_{n}+1) \geq k+n-\sum_{i=1}^{n}N_{i}
& \text{记 } b_{i} = a_{i}-N_{i}+1 ,S= k+n-\sum_{i=1}^{n}N_{i}, \text{则 } b_{i} \geq 1 \end{align} $$

那么可以考虑对总数为 S，种类为 n 的物体进行分隔，最终结果为

$$ C_{S-1}^{n-1} $$

Generating Functions 母函数

Definition

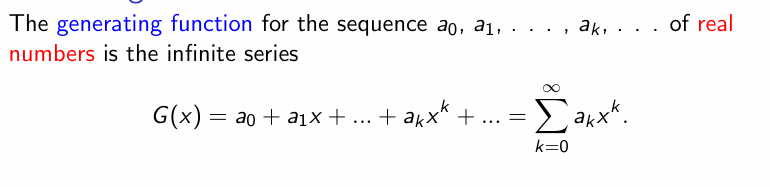
05218285931dde63d6e453cefae6dc9.png
母函数即为形式幂级数，为实系数的无穷级数

将有限数列扩展至母函数形式 ->将后项系数考虑为 0 即可
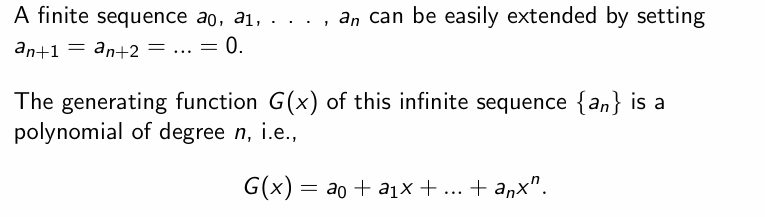
1ce2f34d3fb70803d3fe09216195d4e.png

Useful Facts：常常考虑泰勒级数对母函数的形式进行化简
102139bd1cf1086b3793d58d6533aae.png

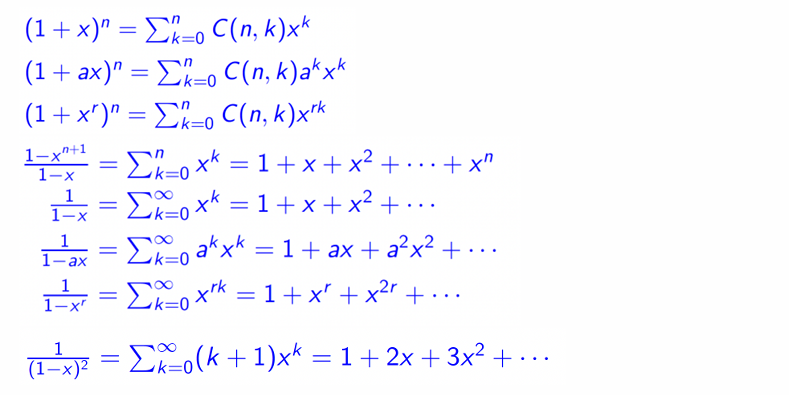
e634c09aad33c368a7932d60fe5ca70.png
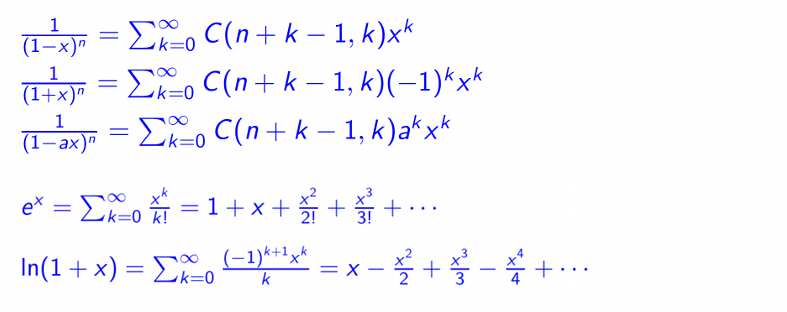
2797cfb1be18e5b7b4890bfee04b291.png

Operations of Generating Functions

Addition & Convolution
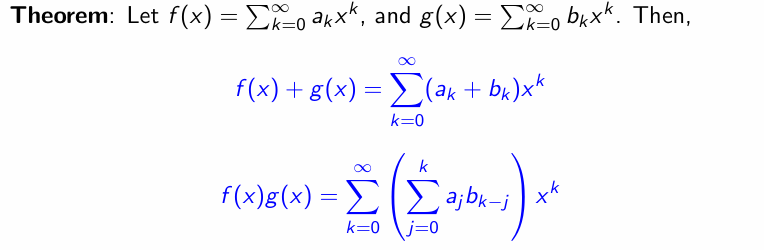
07b65c129d15a0a6177a2adc2e82050.png

补充：Extended Binomial Coeffieicent(二项式系数扩展)
216443afe3a79aa9d7ae0963de7089f.png
fe6e6a3bb4350ee206e2e2088d616d4.png

$$ \begin{pmatrix} -n
r \end{pmatrix} = (-1)^{r}C(n+1-r,r) $$

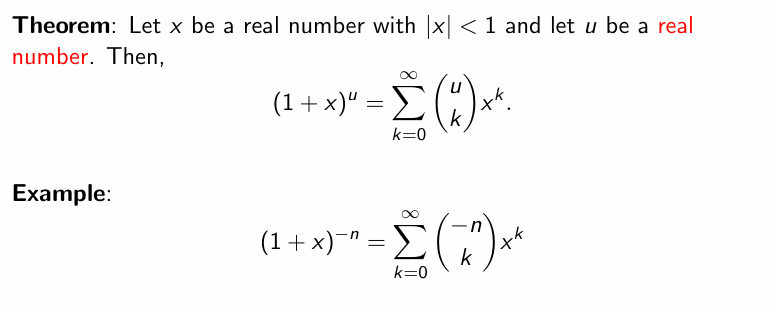
bd00e9b78f06e657cee7104ad6be21e.png

Application

Applied in Combinations with repetitions

核心想法：

  1. 将问题情境建模为带限制的不定方程问题
  2. 通过母函数考虑通过计算多项式的系数转化
    ab4bd53fa55c732a97a30dd8d416331.png

  • Example1
    600837a05e84727b8c1fbf09450a2f8.png

  • Example2: 注意关注序关系是否重要
    5e1e1fb4d71e355bcbd64692941cb76.png
    abfd7dffccc60fbc3fc27910cc5fdda.png

Example3
核心均为考虑如何将计数问题转化为求多项式具体某一项的系数问题
b72638f3dee0eb591508df91096e4ba.png

Solve Recurrence Relation

核心想法：

  1. 生成数列所对应的母函数
  2. 根据数列的递推关系求解母函数，常涉及利用递推性质约简母函数
  3. 得到母函数后通过展开得到数列形式

Example1
c5dc48e5d02b958e3c82f0df2b54b0b.png
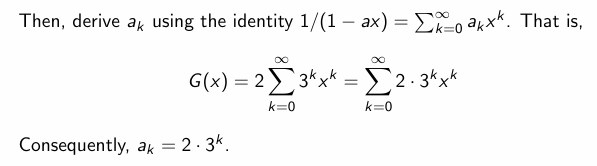
4cc64021a46986899a011ba6f7e850d.png

Example2
505540606c21944e37424d188b27ed7.png
0aee07c8495cbd853bffec6f21e8013.png