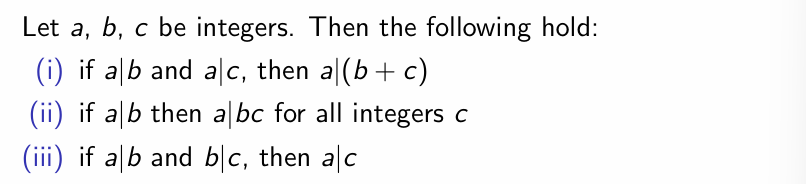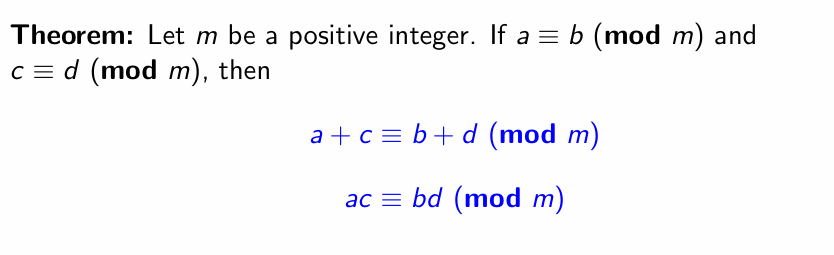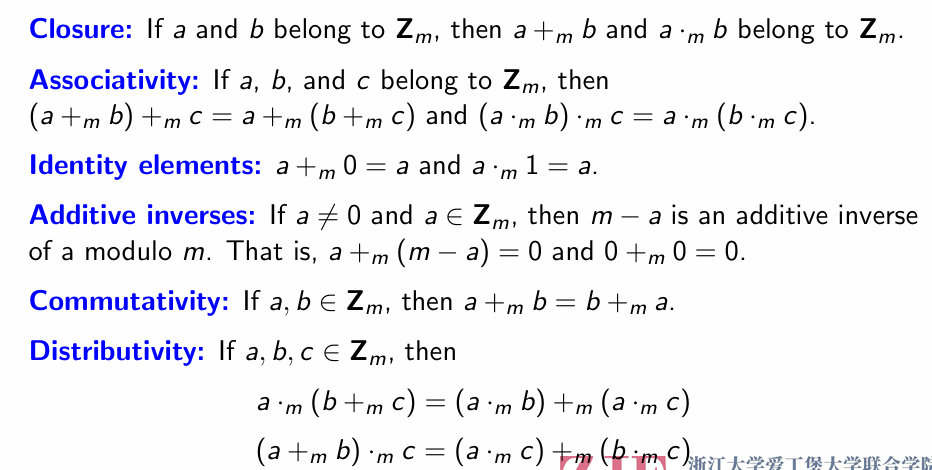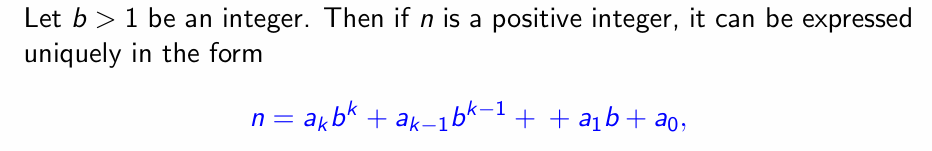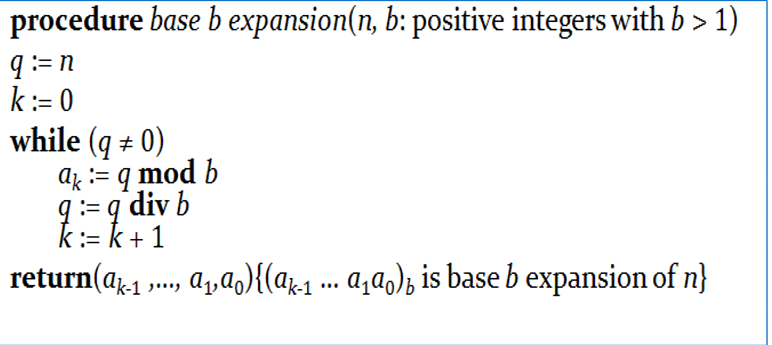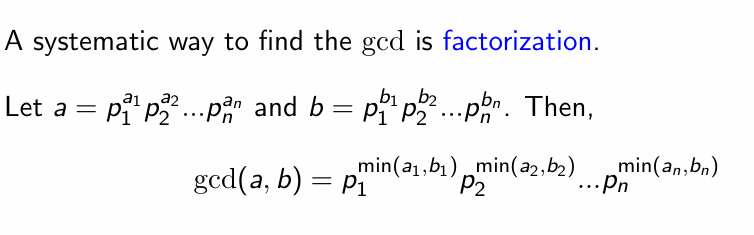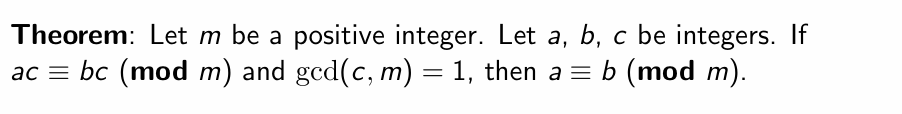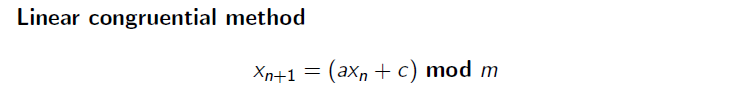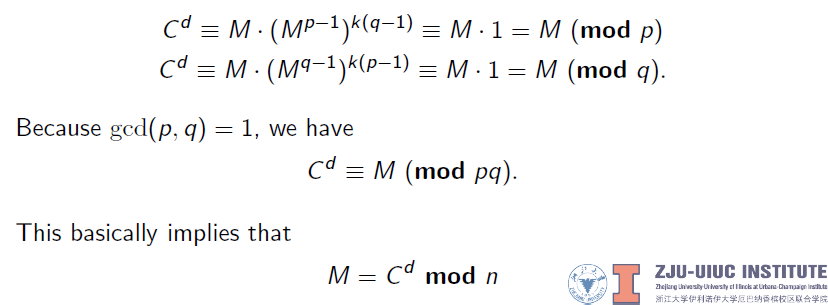Number Theory

#Math213

Basic

Division 整除

• 带余除法
  divisor: 除数， dividend: 被除数， quotient 商，remainder 余数
  

注意带余除法的计算复杂度通过位运算简化可实现 $O(q\log a)$ 量级

• 同余 congruent
  
  
  
• mod m 的剩余系

整数进制表示

Algorithm for Integer Operations

Multiplication

Binary Modular Exponentiation

质数

Prime: 质数
Composite：合数

最大公约数 (GCD) 与最小公倍数 (LCM)

辗转相除求 GCD: 直接写出辗转相除的过程，然后将中间量一步步向前代换，得到 gcd 作为两数线性表示的最小值

裴蜀定理：GCD 为两者的线性表示

注意：可以利用裴蜀定理得出 gcd 的线性表示确定不定方程的解集

线性同余

逆：

• 当 a,m 互素时，存在 a 模 m 的逆
  

• 求解逆：考虑利用 gcd 的线性表示辗转相除
  

中国剩余定理

注意 CRT 解的构造过程：
记

$$M_i=\frac{m}{m_i}$$

对于每一个 $M_i$, 我们考虑其模 $m_i$ 的逆

$$M_i{y}_i\equiv 1(\mathrm{mod}{m}_i)$$

最终若有 $m_i$ 两两互素，我们有模 m 意义下的唯一解：

$$x\equiv \sum _{i=i}^n{a}_i{M}_i{y}_i$$

Crytography

Pseudorandom Number Generators

利用线性同余递推数列生成随机数

Hash Functions

Definition

将任意长度的数据映射到固定长度的数据

Common Solution
直接利用同余函数进行映射

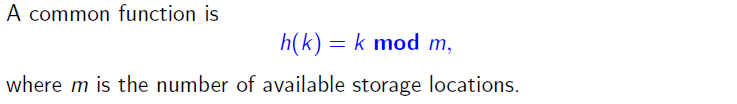
避免同余后的结果映射到相同位置 ->Assign Free Location following the occupied memory location assigned by the hashing function(即将对应的映射结果向后递推)

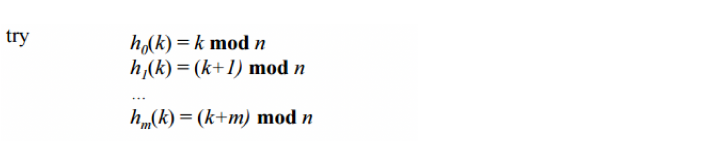
Cryptography

Shift Ciphers

将明文加上偏移量后关注其在完全剩余系中的结果

复杂化 ->考虑引入一个与模互素的数，构造新的完全剩余系

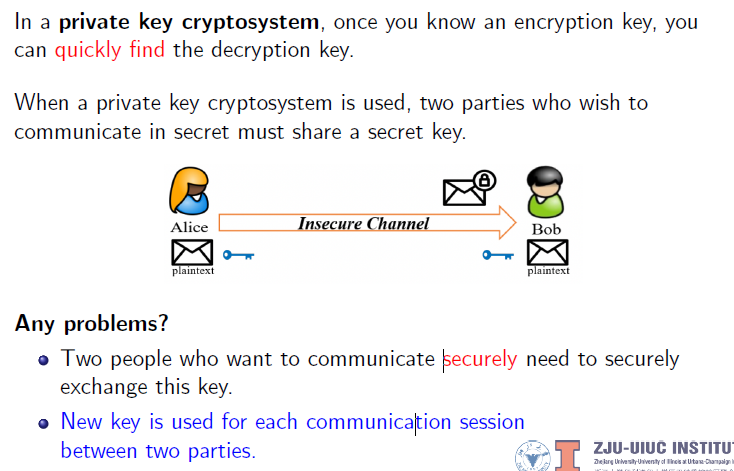
Private/Public Key Cryptosystem

Public Key Cryptosystem

RSA Cryptosystem

• 原理
  
  

公钥：(n,e)
私钥：(d)
注意核心的大素数一定需要保密

• 例子：
  
  

• 应用
  

• 关注原根的概念：素数的原根即为其最小生成整个 modp 完系的生成元

Blockchain