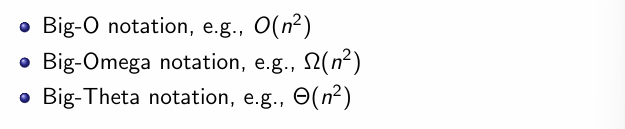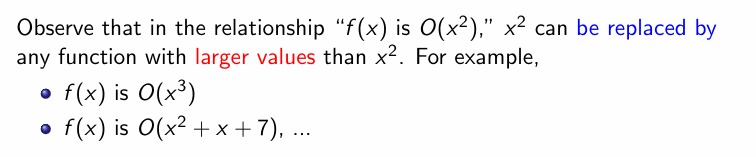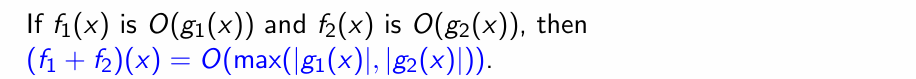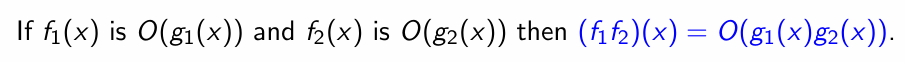#Math213

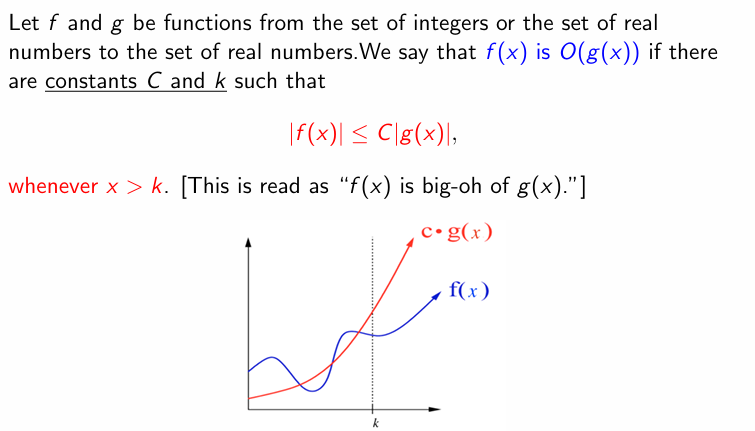
Algorithm

Basic

Definition
4d772fd818c7d4ec51fbd0dc5b2085c.png

Comparison

  • Time Complexity: number of machine operations
  • Space Complexity: amount of memory needed

Instance: 即问题对应的具体输入
e16c147bcaef5e92d86d57bf7e4f8ed.png

Growth of Functions

215dbf6b86353835b64fe37690a9e94.png

  • Big-O Notation
    1e13d2830da65caf17852b2f2c17c82.png
    注意: big-O 只要求量级大于等于即可，意味着只要找到下界，比下界大的函数都可以
    48efb237cf13bcc4f7c6712879c16af.png
    d056fedbaf9453662f37bf48384afe4.png
    注意 $\log(n!)$ 的量级
    证明：

$$ \begin{align} & \text{On the one hand,}
& \log(n!) = \sum_{k=1}^{n}\log(k) \leq n\log(n)
& \text{On the other hand,}
& \log(n!) = \sum_{k=1}^{n}\log(k) \geq \log\left( \frac{n}{2}+1 \right) + \dots +\log(n) \geq \left( \frac{n}{2} \right)\log\left( \frac{n}{2} \right) \end{align} $$

Combination:
40ff5079fa6ccf03bd6a239d227172b.png
661d09c8cf949b472e4c5debad058d3.png

  • Big-Omega Notation
    63b9277d189763ce3df51cc606f4345.png

Big-Omega: tells us a lower bound of growth rate

a3602fdb0cfedd5451f27f092898dbe.png

  • Big-Theta Notation
    c00b6b28f5ddb6c19ad2e5dc18c92dd.png
    同时控制上界与下界，两函数量级相同

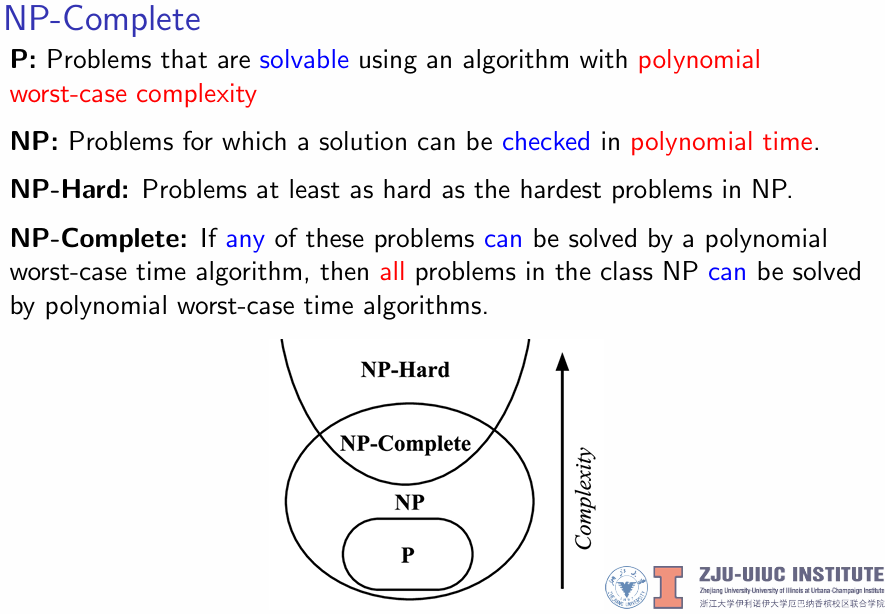
Complexity

88aed10be9d2d106cb7a9a462945117.png

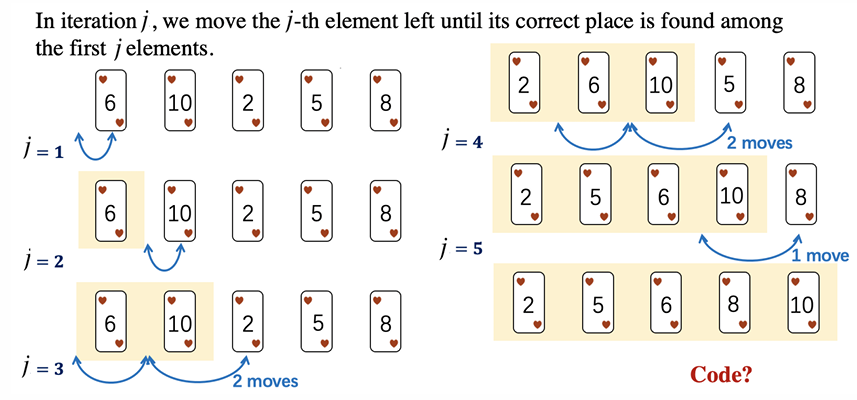
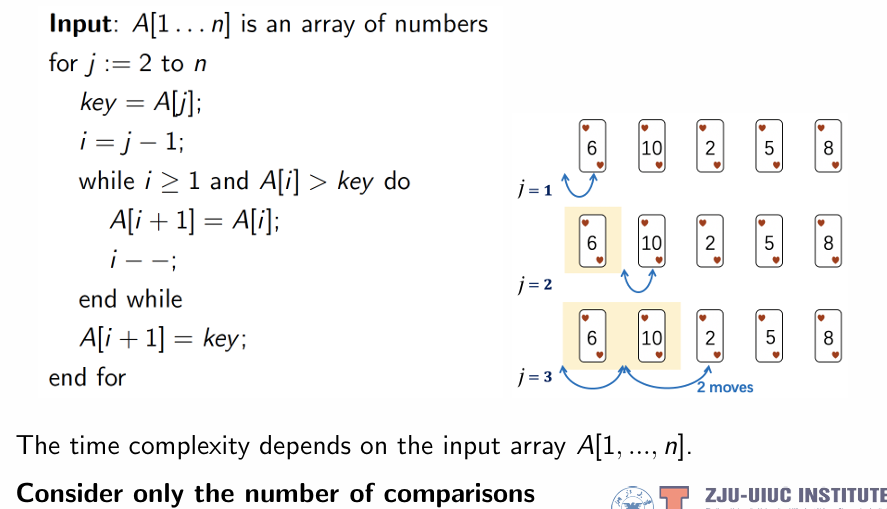
Example

Insertion Sort:
270b327ed0cfeffd9ccbf762a9e0b7b.png
0dacde263c5b7150f3f8d47d7f91234.png
4ac4b1431dbd96c39717f81aaec2c82.png

对于 Average Complexity: 考虑所有情况等可能，计算其复杂度均值（一般情况下难以计算）

NP-Complete

7dbf352960f131dcd9cff8e54f25d0f.png