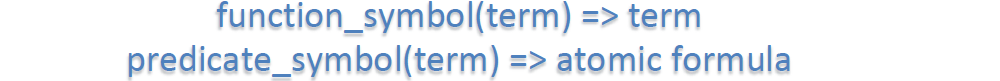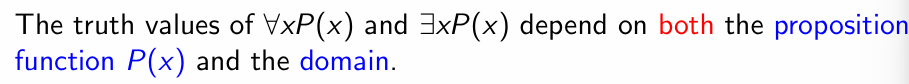#Math213

Predicate

Definition

cb061344c3406784c079cb1159acab7.png

  • 核心即为包含变量的论断（注意只有当变量的取值都确定时才能算命题）
  • Domain: 所有变量可能取值的集合
  • 真值集合即为所有使 P 为真的变量取值组合
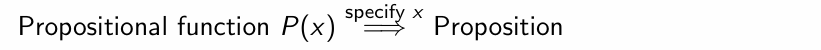
    dd1013a5590557e9dc30ec1a20d2027.png
    Basic components of predicate logic:
    1. term(逻辑表达式的基本单位，代表个体或者对象)
    2. functional symbol(基于一个或多个 term 作为输入，构造映射输出)
    3. predicate symbol(用于表达陈述)
    4. quantifier and logical connectives
      d1815a3c2194e40807d85ae89a12462.png

4475da030537597b53a4b9632308136.png

Quantified Statements

Types of quantified statements

  • Universal Quantifier 全称量词: $\forall$ For all x P(x)
  • Existential Quantifier 存在量词: $\exists$ There exists an element x in the domain such that P(x)
    Notice: when the domain is empty, $\forall xP(x) \cup \exists xP(x)$ are false
    $\forall xP(x) \text{and}\ \exists xP(x)$ are propositions

Property

6492936a7959e15ee6157e6326a2272.png
8cac60572318561c4151b3bb66c34c0.png

任意与存在的转化
1453c215c909c83cd393951676adc7a.png

Nested Quantifiers

Basics

  • Definition :
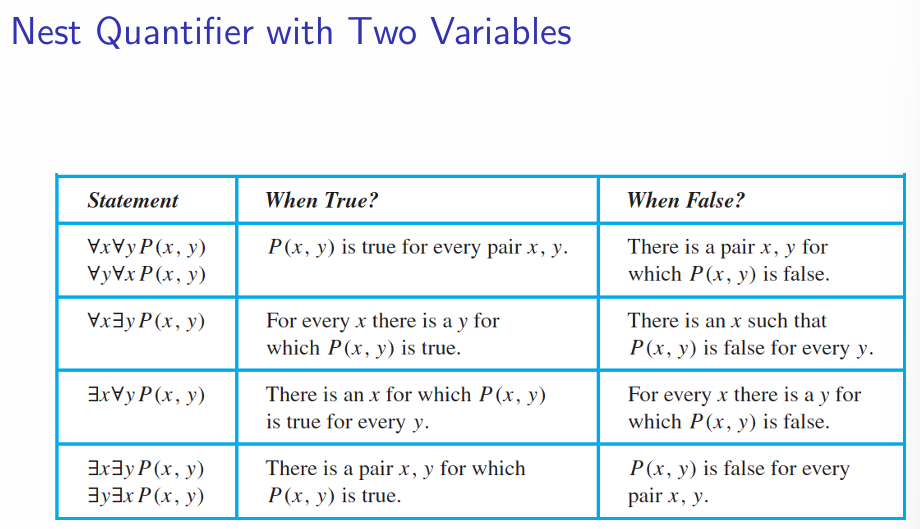
    More than one quantifier may be necessary to capture the meaning of a statement in the predicate logic.
  • Order of Quantifiers:
    The order matters if quantifiers are of different type.
    The order doesn’t matter if quantifiers are of the same type.
    0804d5755be41e92b567b6caf9b8684.png
  • Negating Nested Quantifier
    b54df4cc160e642bad9d2004425f044.png

Mathematical Proofs

Argument

Definition

A sequence of propositions that end with a conclusion
An argument if valid if the truth of all its premises implies that the conclusion is true(对于 Valid Argument 而言，只要前置条件均满足，结论一定正确)
082ec100b8a38528bfca27a1b94026b.png

Rules of Inference

73eb07dc2e95e3628e81d01c51ab331.png
f5e30b76a91a1a7e0ef40150bab341a.png
3715f57bc6b5a31c779910878f73f0b.png
057df7d61e2532bebdb8b98632c40c3.png

Rules of Inference for Quantified Statements
c0a580eef6c36f4fad489b2b740f5ad.png

Proof

Concept

d31bc1f05de7646335aa8c9117b7b1e.png

Proof Type & Method

Formal and Informal
  • Formal: follow logically from the set of premises, axioms, lemmas, and other theorems
  • Informal: steps are not expressed in any formal language of logic; steps may be skipped; the axioms being assumed and the rules of inference used are not explicitly stated.
Methods of Proving Theorems

aaa82d91f2b92ddbd4f44cd901eea43.png

  • Vacuous Proof: 假设论证的大前提恒假
    32cfb8536b9332f51c0f07f4f4bf91b.png
  • Trivial Proof: 假设结论恒真，证明推出的关系恒真
    7ac3e49ae768aa2b5c7f7785906b78f.png
  • Quantifiers Proof