Logic
#Math213
Terms
Logic
Logic is the basis of all mathematical reasoning:
- Syntax of statements
- The meaning of statements
- The rules of logical inference
Proposition(命题)

注意:
- 命题不能是一个疑问句或者命令;
- 命题要么真要么假,不能涉及变量,命题一定能判断真假
Compound Propositions: Combinations of several propositions
Logical Connectives

- 注意 p->q 的各种表述unless 与 only if
注意 p->q 准确应理解为 p 蕴含于 q (Not p; p implies q)

- 逆命题 (converse),反命题 (inverse),逆否命题 (contrapositive)


- Biconditional 的表述
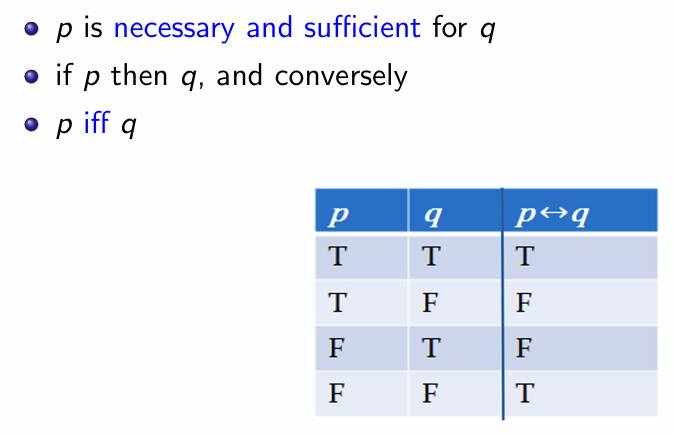
Propositional Application and Equivalence
Application

Equivalence
Specific Terms
- Tautology: 恒真
- Contradiction: 恒假

Logical Equivalences
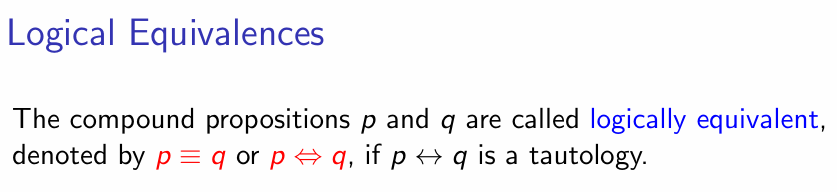
等价 ->Truth Table 上两个命题同真同假即可
等价的证明
- truth table 上证明同真同假
- 直接用逻辑算符证明
Boolean Logic
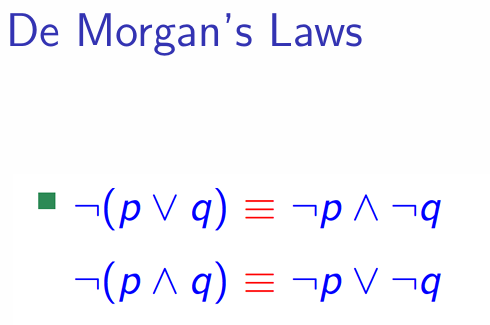

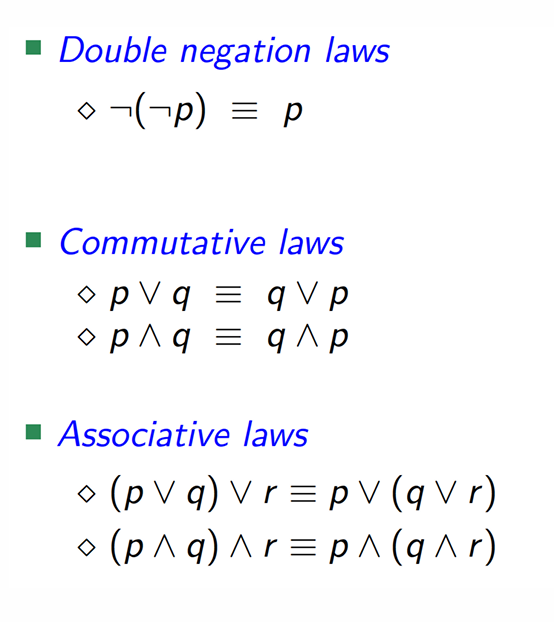

Proof
- Logical Expression
- Truth Table
Limitation of Propositional Logic
引入 Predicates(断言/谓词) 与 quantifier(量词)