MATH 213 Collection

汇总表格

table date
from #Math213
sort date

集萃

逻辑

1. 命题

命题不能是一个疑问句或者命令；
命题要么真要么假，不能涉及变量,命题一定能判断真假
逆命题 (converse),否命题 (inverse),逆否命题 (contrapositive)
对于 $p \to q$
converse: 条件结论交换 $q \to p$
contrapositive: 条件结论交换并且同时取反 $\neg q \to \neg p$ (注意逆否命题与原命题同真同假)
inverse: 条件结论同时取反 $\neg p \to \neg q$

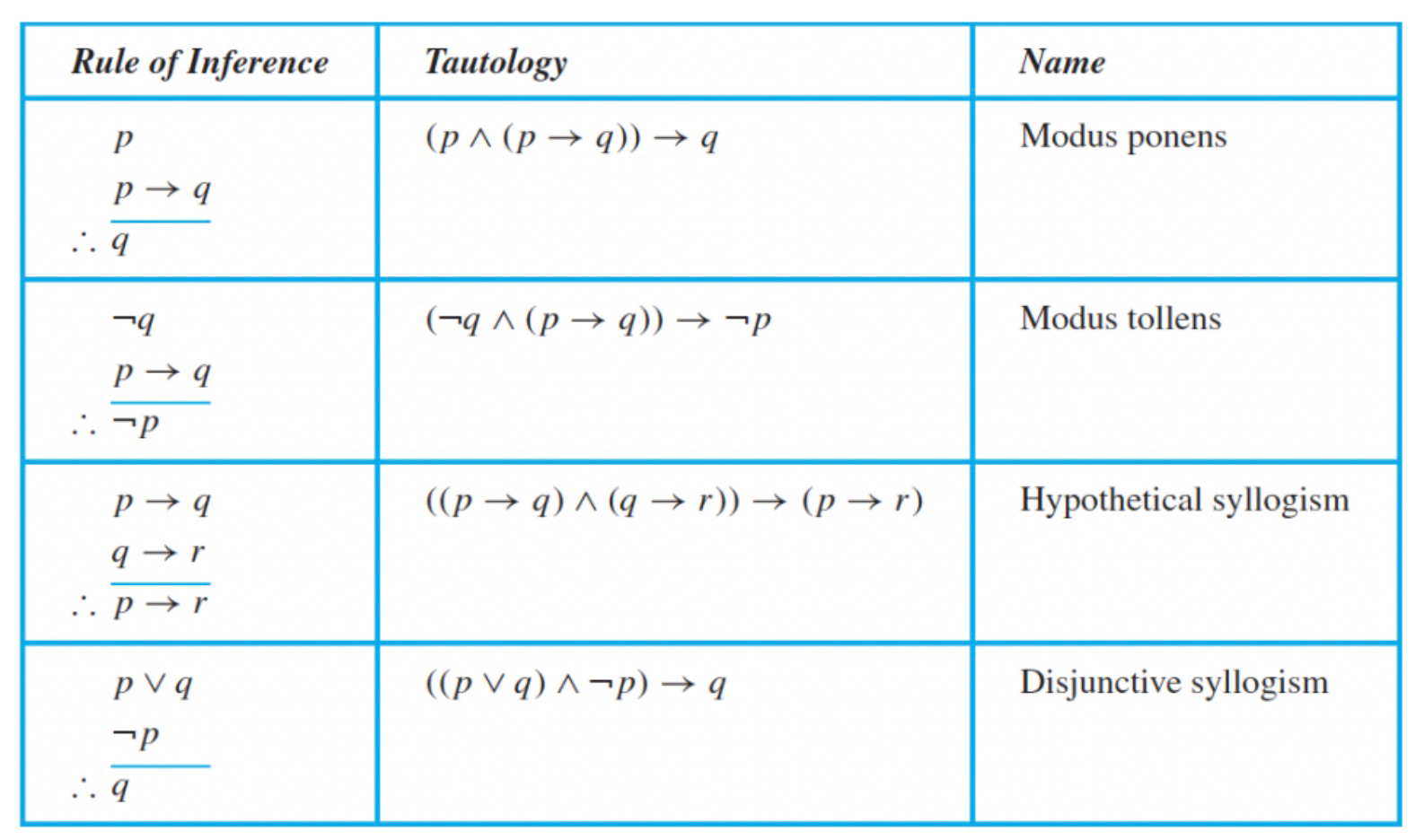
2. 逻辑连接词

重点领会 p->q:(Not p; p implies q)

$p \to q \equiv \neg p \cup q$

注意 p->q 准确应理解为 p 蕴含于 q (Not p; p implies q)

Biconditional 的表述

p is necessary and sufficient for q（充分必要条件）
if p then q, and conversely $(p \to q) \cap (q \to p)$
p iff q

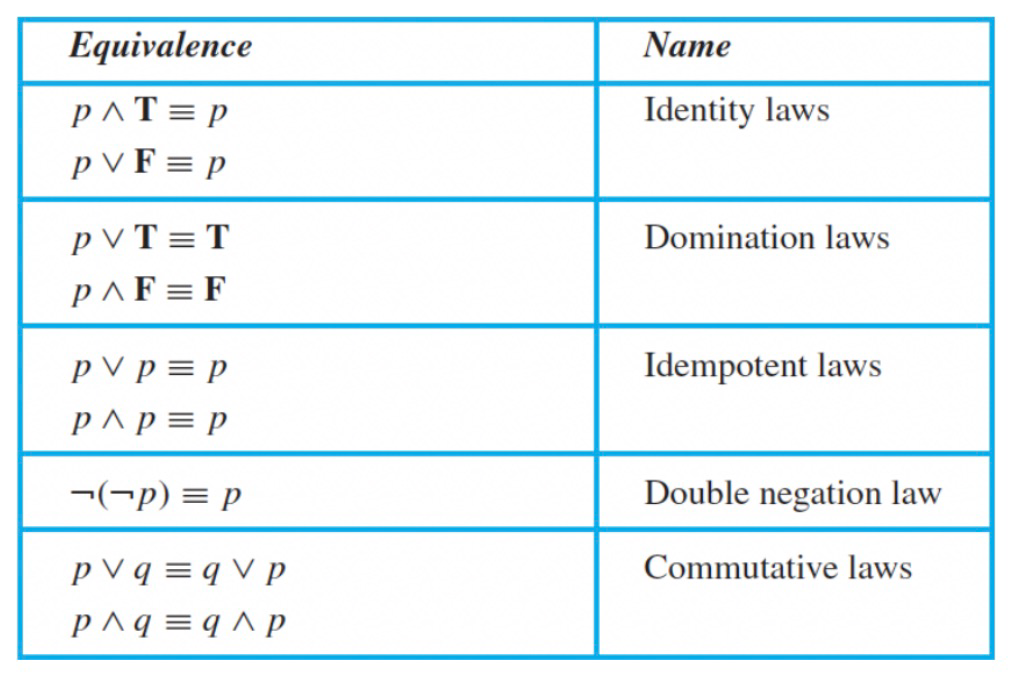
3. 等价性

Tautology: 恒真
Contradiction: 恒假
Contigency: 既非恒真又非恒假
逻辑等价性

$p \equiv q 或 p \leftrightarrow q$

证明:

利用 truth table
直接利用逻辑算符证明，证明两边的推出关系均成立
Boolean Logic
重点关注 De Morgan’s Laws 与 Distributive Laws

4. Predicate Logic & Quantified Statements 谓词逻辑与量化命题

谓词逻辑

核心即为包含变量的论断（注意只有当变量的取值都确定时才能算命题）
Domain: 所有变量可能取值的集合
真值集合即为所有使 P 为真的变量取值组合
命题函数 $P (x)$ 是一个含有变量 x 的表达式，当给 x 赋予具体的值时， $P (x)$ 成为一个命题

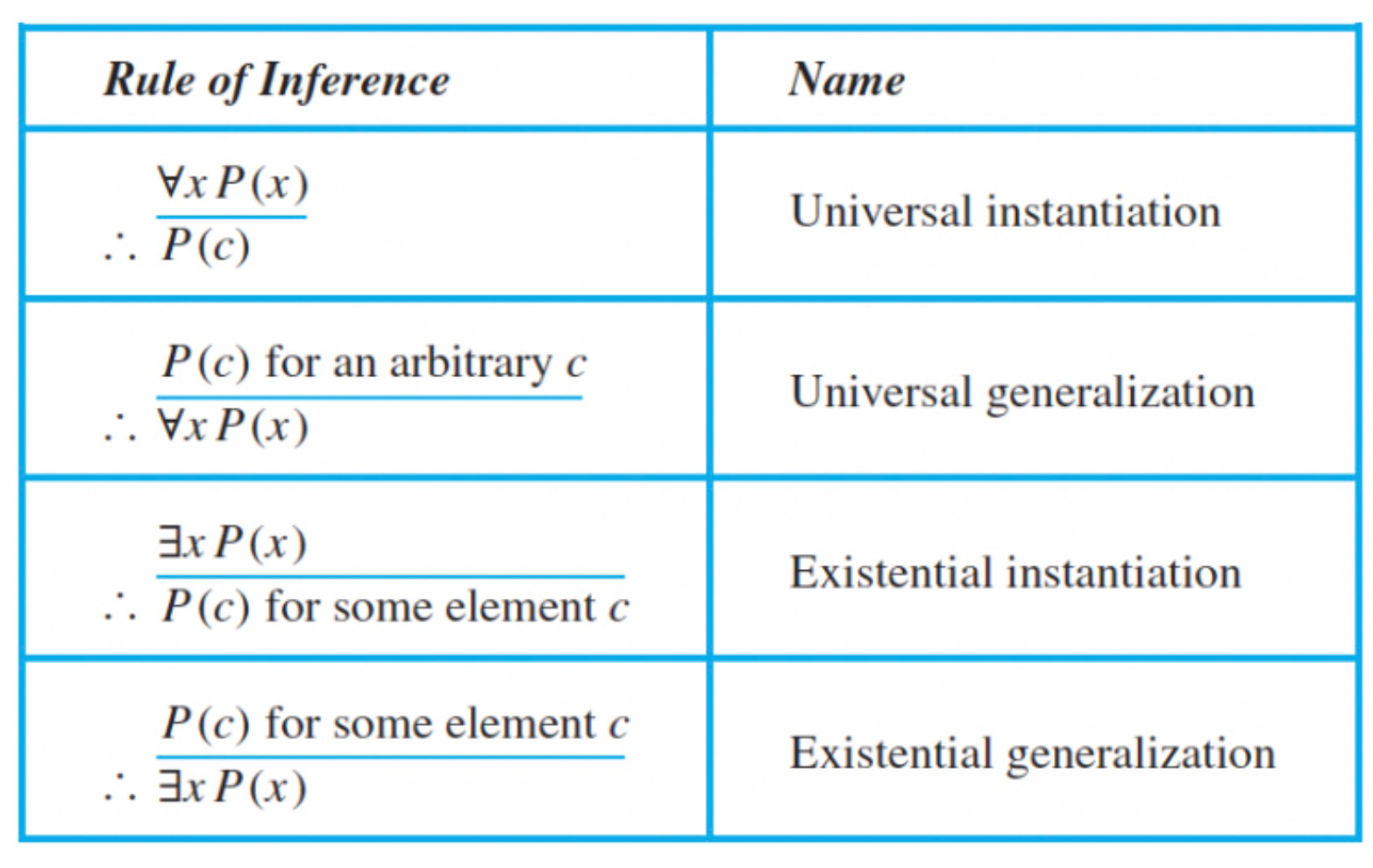
量化命题
Types of quantified statements

Universal Quantifier 全称量词: $\forall$ For all x P(x)
Existential Quantifier 存在量词: $\exists$ There exists an element x in the domain such that P(x)
Notice: 当定义域为空集时, $\forall x P (x) \cup \exists x P (x)$ 均错误
$\forall x P (x) and \exists x P (x)$ are propositions

任意与存在的转化：

$\begin{aligned} \neg (\exists x P (x)) \equiv \forall x \neg P (x) & \neg (\forall x P (x)) \equiv \exists x \neg P (x) \end{aligned}$

量词的顺序：

当量词的种类不同时，不能交换量词的顺序 (order matters)
当量词的种类相同时，可以交换量词的顺序 (order doesn’t matter)

5. 证明

集合与函数

1. 基本概念

集合：一组无序的对象
集合的势 (cardinality)：集合中的元素个数
幂集 (power set)：集合所有子集的集合
元组 (tuple): 有序的集合
笛卡尔积 (Cartesian Product): 各集合元素的有序组合形式的多维组的集合
关系 (Relation): 笛卡尔积的子集

2. 单射、满射与双射
考虑函数 $f : A \to B$

Injective, One-to-one 单射函数，不同的像对应不同的原像
一个函数 f 单射当且仅当对于其值域中的所有 $x$ 和 $y$ , 若 $f (x) = f (y)$ , 则 $x = y$
Surjective, Onto 满射函数，陪域中的每一个元素均有像与之对应
一个函数称为满射，如果对于 $B$ 中的每一个元素 $b$ 均存在 $A$ 中的元素 $a$ 使得 $f (a) = b$
Bijective, one-to-one correspondence 双射函数
既为单射又为满射
证明双射 ->分别证明单射与满射即可

3. 逆函数与复合函数

4. 集合的势

[!tip] 总结

可数集：集合为有限集或者为可数无限集（与正整数集的势相同，即集合中的元素可以按照一定顺序列举出来）

有理数集 $Q$ （可以考虑控制分子分母的和，然后逐项列举）, 代数集可数

不可数集：集合中的元素不能按照一定顺序列举

实数集 $R$ （考虑康托尔对角线）, 任意区间（可以与实数集建立双射）

证明集合的势相等：考虑构造相互的单射

Complexity of Algorithms

1. Growth Rate

常见函数的增长率估计

注意 $\log (n!)$ 的量级
证明：

$\begin{aligned} On the one hand, & \log (n!) = \sum_{k = 1}^{n} \log (k) \leq n \log (n) & On the other hand, & \log (n!) = \sum_{k = 1}^{n} \log (k) \geq \log (\frac{n}{2} + 1) + \dots + \log (n) \geq (\frac{n}{2}) \log (\frac{n}{2}) \end{aligned}$

2. 常见算法

计算多项式的值 Horner’s Algorithm: $O (n)$
插排：最坏情况为 $O (n^{2})$

数论：

带余除法记号与复杂度
divisor: 除数， dividend: 被除数， quotient 商，remainder 余数

基本算法
[[ Number Theory#Algorithm for Integer Operations ]]
gcd 性质
基本内涵：从素因子最大公共幂次考虑；从两者最小正线性表示考虑
1. 辗转相除求 gcd(a,b)
不断重复重复带余除法的过程，记录每次的系数
从最终的余数向上回代，将 gcd 表示为原始 a,b 的线性组合
还可以利用 gcd 的线性表示解相应的不定方程/利用辗转相除求解逆

例如：

中国剩余定理

汇总表格

集萃

逻辑

集合与函数

Complexity of Algorithms

数论：

反向链接：