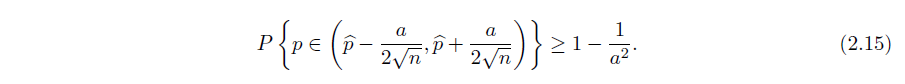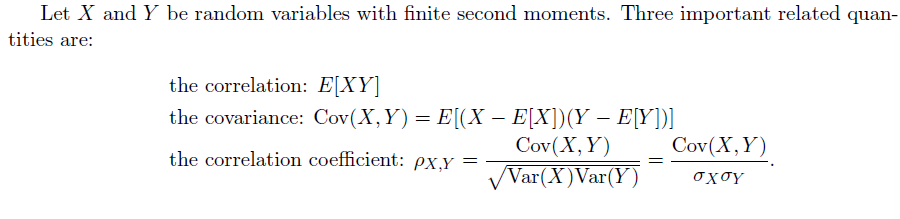表格汇总

table date, categories
from #ECE313
sort date

参考资料

复习纲要

概率基础

1. 期望与方差

4d051adaa84ab3ca573e65b6ee9225c.png

注意方差与标准差的关系
a7be42645f2aad20b287c092a7f4aeb.png

2. 条件概率

$$ \begin{align} & P(B|A)= \frac{P(AB)}{P(A)} \text{ if } P(A)>0
& P(ABC) = P(C)P(B|C)P(A|BC) \end{align} $$

3. 独立事件与独立变量

$$ \begin{align} & P(AB)=P(A)P(B)
& P(A^{c}B)= P(B)-P(AB) \end{align} $$

注意衡量多个独立事件是否独立时，他们的任意子集均需满足独立事件的条件

4. 最大似然估计
核心即为在

  • 给定观测结果情况下估测最大可能的对应参数
  • 给定参数估计最大可能的观测结果

对于连续性随机变量的 ML Parameter Estimation: 我们依然考虑选取能使对应采样结果最大所对应的参数，其中对应采样结果的参数概率通过在临近区间内积分确定

$$ f_{\theta}(u) \approx \frac{1}{\epsilon}P\left{ u-\frac{\epsilon}{2} < X < u + \frac{\epsilon}{2} \right} $$

5. 不等式与估计

  • 马尔可夫不等式：估计非负随机变量的均值

$$ P(Y\geq c) \leq \frac{E[Y]}{c} $$

  • 切比雪夫不等式：利用方差估计分布的均匀性（注意与置信区间与中心极限定理的结合）

$$ P(|X-\mu |\geq d) \leq \frac{\sigma ^{2}}{d^{2}} $$

  • 置信区间
    考虑用小样本对实际情况建模，将其模拟为二项分布
    949c225a7f6c5ee1f06ee30fc2d74cf.png
    5d5b40be30f5bf4f5cb7330948d7ca6.png

6. 全概率定律与贝叶斯定理

  • 全概率定理：对整个概率空间选取某一组事件的划分

$$ P(A) = P(AE_{1})+\dots P(AE_{k}) = P(A|E_{1})P(E_{1})+\dots+P(A|E_{k})P(E_{k}) $$

  • 贝叶斯公式

$$ P(E_{i}|A) = \frac{P(AE_{i})}{P(A)} = \frac{P(AE_{i})}{P(AE_{1})+\dots P(AE_{k})} $$

利用全概率定理计算均值

$$ \begin{align} & E[X|A] = \sum_{i}u_{i}P(X=u_{i}|A)
& E(g(X)|A) = \sum_{i}g(u_{i})P(X=u_{i}|A)
& E[X] = \sum_{j=1}^{J}E[X|E_{j}]P(E_{j}) \end{align} $$

7. Binary Hypothesis
每一种假设对应离散型随机变量不同的概率密度函数，最终构成一个似然矩阵。注意两种假设互斥，但不一定成立，系统最终的输出结果根据确定的 decision rule 既可能 $H_{1}$ 也可能为 $H_{0}$

$$ \begin{align} & p_{false alarm} = P(\text{declare H1 true| H0})
& p_{miss} = P(\text{declare H0 true| H1})
& p_{e} = \pi_{0}p_{false alarm} +\pi_{1}p_{miss}
& \text{先定义ratio } \Lambda(k) = \frac{p_{1}(k)}{p_{0}(k)} = \frac{f_{1}(u)}{f_{2}(u)} \end{align} $$

注意对于离散型与连续型随机变量都可以从 Ratio 角度得到最终结果
对于连续性随机变量，求 false alarm 与 miss 时即为考虑在对应 X 的区间范围内 pdf 的积分

  • ML 最大似然决定 ->哪种假设对应的变量取值概率即选
    $\Lambda(X)>1$ -> declare $H_{1}$ is true
    $\Lambda(X)<1$ -> declare $H_{0}$ is true
  • MAP: 考虑引入先验概率，再根据后验概率大小决定

$$ \begin{align} & P(H_{i},X=k) = \pi_{i}p_{i}(k)
& \tau = \frac{\pi_{0}}{\pi_{1}} \end{align} $$

8. Union bound 估计
考虑容斥原理，有

$$ P(A \cup B) \leq P(A)+P(B) $$

核心为将代求事件表示为一些事件的并集进行上界估计

例题:
74babbb59b230e27adfc6ab9220db66.png

9. 大数定理
LLN 建模基于的情境：
给定一系列均值相同的独立（或弱相关的）的随机变量，同时对随机变量的规模有一定要求，LLN 认为当随机变量个数趋于无穷时，他们和的均值收敛于一个定值

10. 中心极限定理

认为多个独立相同分布的随机变量（均值与方差均有限），他们和的分布标准化后趋于高斯分布
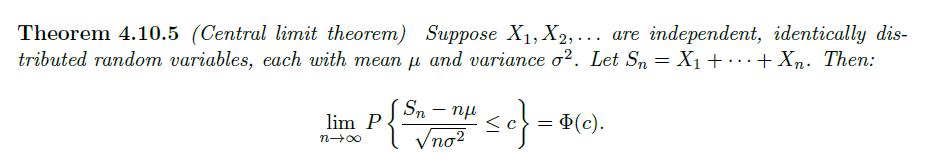
8ac7455a4a0510a38d6b3c9c996db9f.png

应用 1：利用 CLT 近似二项分布（因为其可以表示为多个伯努利分布的和）
注意有时需要对高斯近似用 Continuity Correction

$$ \begin{align} & P(X\leq k) \approx P(\tilde{X}\leq k+0.5)
& P(X\geq k) \approx P(\tilde{X}\geq k-0.5)
& P(X=k) \approx \int_{k-0.5}^{k+0.5}f_{X}(u)du \end{align} $$

离散型随机变量

1. 伯努利分布：两点分布

$$ \begin{align} & P(X=1) = p, &P(X=0) = 1-p
& E[X] = p, &Var(X) = p- p^2 \end{align} $$

2. 二项分布: n 次独立的伯努利实验,考察 1 出现的次数的概率

$$ \begin{align} & p_{X}(k) = C_{n}^{k}p ^{k}(1-p)^{n-k}
& E[x] = np, Var(X) = np(1-p)
& \sum C_{n}^{k}p ^{k}(1-p)^{n-k} =1 \end{align} $$

3. 几何分布：进行一系列伯努利实验首次出现 1 进行的实验次数对应的概率

$$ \begin{align} & \sum_{k=1}^{\infty}(1-p)^{k-1}p=1
& p_{L}(k)=(1-p)^{k-1}p, \ P(L>k) = (1-p)^{k}
& E[L] = \frac{1}{p}, \ Var(L)=\frac{1-p}{p ^{2}}
& \text{Memoryless Property: } P(L>k+n|L>n) = P(L>k) \end{align} $$

4. 伯努利过程与负二项分布
考虑进行无限次伯努利实验，得到 $j$ 个 1 所累积进行的实验次数 $S_{j}$
考虑 $S_{r}$ 所满足的概率分布为负二项分布,参数为 r,p

$$ \begin{align} & p(n) = C_{n-1}^{r-1}p^{r}(1-p)^{n-r}
& E[S_{r}] = rE[L_{1}] = \frac{r}{p}
& Var(S_{r}) = rVar(L_{i}) = \frac{r(1-p)}{p ^{2}} \end{align} $$

5. 泊松分布 -> 对于 n 很大 p 很小的二项分布进行近似

近似时考虑 $np=\lambda$，近似原理考虑二项分布 n 趋于无穷情况

$$ \begin{align} & p(k) = \frac{e^{-\lambda}\lambda ^{k}}{k!}
& E[Y] = \lambda, Var(Y) = \lambda \end{align} $$

连续型随机变量

1. pdf 与 cdf
记累计分布函数 CDF 为 $F_{X}$, 概率密度函数为 $f_{X}$ 则我们有
当 CDF 取值连续时，我们有任意点取值的概率均为 0

$$ \begin{align} & F_{x}(c) = P{\omega:X(\omega)\leq c} = P(X\leq c)
& F(x-) = \lim_{ y \to x, y<x }F(y) , F(x+) = \lim_{ y \to x, y>x }F(y)
& \Delta F_{X}(x) = F_{X}(x)-F_{X}(x-)
& P(X=c) = \Delta F_{X}(c),\ P(X<c) = F_{X}(c-) \end{align} $$

如何推导 CDF 及其对应的 PDF->考虑先根据事件定义求出 CDF 再微分求 PDF

$$ F_{X}(c) = \int_{-\infty}^{c}f_{X}(u)du $$

基于 CDF 与 PDF 的概率与均值方差

$$ \begin{align} & P(a<X\leq b) = F_{X}(b)-F_{X}(a)
& E[X] = \int_{-\infty}^{\infty} uf_{x}(u)du
& Var(X) = E[X^{2}] - E^{2}[X]
& Var(g(X)) = \int_{-\infty}^{\infty}g(u)^{2}f_{X}(u) \, du - \left( \int_{-\infty}^{\infty}f_{X}(u)g_{X}(u) \, du \right) ^{2} \end{align} $$

2. 均匀分布 ->在支持集上 pdf 为常数

$$ \begin{align} & f_{X}(u) = \frac{1}{b-a}, a\leq u\leq b
& E[X] = \frac{a+b}{2}, \ Var(X) = \frac{(a-b)^{2}}{12}, \ E[X^{k}] = \frac{1}{k+1}
\end{align} $$

3. 指数分布 ->几何分布连续时取极限的情况

$$ \begin{align} & f_{T}(t) = \lambda e^{-\lambda t}, t\geq 0
& F_{T}(t) = 1-e^{-\lambda t}, t\geq 0
& E[T^{n}] = \frac{n!}{\lambda ^{n}}, \ E[T] = \frac{1}{\lambda}, \ Var(T) = \frac{1}{\lambda ^{2}}
& \text{Memoryless Property: } P(T>s+t|T>s) = e^{-\lambda t} = P(T>t) \end{align} $$

将 $\lambda$ 理解为失败概率, 转化有 $p=\lambda h$
4. 泊松过程
指数分布本质上为几何分布的极限 ->泊松过程本质上为伯努利过程的极限

  • $U_{j}=hL_{j}$ 前 $j-1$ 次 count 与 $j$ 次 count 之间的时间间隔，服从 exponential distribution,参数为 $\lambda=\frac{p}{h}$
  • $N_{t}=C_{\frac{t}{h}}$ 时间为 t 时出现的 count 次数，服从于二项分布，近似为泊松分布，均值为 $\lambda t$
  • $T_{j}=hS_{j}$ 为出现 j 次 count 所用的时间
    性质: 对于参数为 $\lambda$ 的泊松过程，我们有
  • N 的增量相互独立 -> $N_{t}-N_{s}$ 满足 $Poi(\lambda(t-s))$ （泊松分布）
  • 相邻的 count 所用时间 $U_{1},U_{2},\dots$ 相互独立，满足参数为 $\lambda$ 的指数分布

5. 埃尔朗分布
$T_{r}$ 记为泊松过程中 $r^{th}$ count 所用的时间， $T_{r}=U_{1}+\dots+U_{r}$, 其中 $U_{1},\dots,U_{r}$ 为相互独立的指数分布随机变量，参数为 $\lambda$, 可以理解为 r 个独立随机过程的加和

$$ \begin{align} & f_{T_{r}}(t)=\frac{e^{-\lambda t}\lambda ^{r}t^{r-1}}{(r-1)!}
& E(T_{r}) = \frac{r}{\lambda}
& Var(T_{r}) = \frac{r}{\lambda ^{2}} \end{align} $$

6. Linear Scaling 与高斯分布

  • 对于线性变换 $Y=aX+b$,我们有

$$ \begin{align} & f_{Y}(v) = f_{X}\left( \frac{v-b}{a} \right) \frac{1}{a}
& F_{Y}(v) = P(aX+b\leq v) =F_{X}\left( \frac{v-b}{a} \right)
& E[Y] =aE[X]+b, \ Var(Y) = a^{2}Var(X) \end{align} $$

  • 高斯分布：对于一般的高斯分布 $Y \sim N(\mu, \sigma)$

$$ f_{Y}(v) = \frac{1}{\sqrt{ 2\pi }\sigma}e^{-(v-\mu)^{2} / 2\sigma ^{2}} $$

$\Phi(u)$ 表示对于标准正态分布从负无穷积到 u 的概率
$Q(u)$ 表示对于标准正态分布从 u 积到正无穷的概率
注意不同 $\sigma$ 对应的分布概率 68.3 -> 95.5 -> 99.7

$$ Q(u) = 1 - \Phi(u) = \Phi(-u) $$

当计算非标准正态分布的概率时，常常通过 Linear Scaling 返回到标准正态函数利用 $\Phi$ 或者 $Q$ 计算

$$ \begin{align} & P(Y \leq u) = P\left( \frac{Y-\mu}{\sigma} \leq \frac{u-\mu}{\sigma} \right) = \Phi\left( \frac{u-\mu}{\sigma} \right)
& P(Y > u) = 1 - \Phi\left( \frac{u-\mu}{\sigma} \right) \end{align} $$

联合分布随机变量

基础

1. 联合 CDF

$$ \begin{align} & F_{X,Y}(u_{0},v_{0}) = P{X\leq u_{0},Y\leq v_{0}}
& P((X,Y)\in R) = F_{X,Y}(b,d)-F_{X,Y}(b,c)-F_{X,Y}(a,d)+F_{X,Y}(a,c) \end{align} $$

2. 联合 pmf 或 pdf
离散型 ->联合 pmf

$$ \begin{align} & P_{X,Y}(u,v) = P(X=u,Y=v)
& \text{Marginal pmf }\ p_{X}(u) =\sum_{j}p_{X,Y}(u,v_{j})
& \text{Conditional pmf } P_{Y|X}(v|u_{0}) = P(Y=v|X=u_{0}) = \frac{P_{X,Y}(u_{0},v)}{P_{X}(u_{0})} \end{align} $$

连续型 ->联合 pdf

$$ \begin{align} & F_{X,Y}(u_{0},v_{0}) = \int_{-\infty}^{u_{0}}\int_{-\infty}^{v_{0}}f_{X,Y}(u,v) dudv
& \text{Marginal pdf } f_{X}(u) = \int_{-\infty}^{\infty}f_{X,Y}(u,v)dv =\int_{-\infty}^{\infty}f_{Y}(v)f_{X|Y}(u|v)du
& \text{Conditional pdf } f_{Y|X}(v|u_{0}) = \frac{f_{X,Y}(u_{0},v)}{f_{X}(u_{0})} \end{align} $$

3. 期望

$$ \begin{align} & E[g(X,Y)] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(u,v)f_{X,Y}(u,v)dudv
& E[X] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}uf_{X,Y}(u,v)dudv
& E[Y] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}vf_{X,Y}(u,v)dudv \end{align} $$

条件期望: 注意 $E[Y X=u]$ 可以视为关于 $u$ 的函数，则 $E[Y X]$ 可以视为关于 $X$ 的函数

$$ E[Y|X=u] = \int_{-\infty}^{\infty}vf_{Y|X}(v|u)dv $$

31f18ceb8e55440261b69c35f9c9b3d.png
4. 独立性
两随机变量相互独立的条件：

$$ \begin{align} & \text{CDF: } F_{X,Y}(u_{0},v_{0})=F_{X}(u_{0})F_{Y}(v_{0})
& \text{PDF: } f_{X,Y}(u,v)=f_{X}(u)f_{Y}(v)
& \text{条件概率角度，充要：}
& f_{Y|X}(v|u) =f_{Y}(v) \

\end{align} $$

X,Y 为相互独立的联合分布连续随机变量，则 $f_{X,Y}$ 支撑集为 product set

Joint pdfs of functions of random variables

  • 线性变换 $\begin{pmatrix}W \Z\end{pmatrix}=A\begin{pmatrix}X \Y\end{pmatrix}$

$$ f_{W,Z}(\alpha,\beta) = \frac{1}{|\det A|}f_{X,Y}(A^{-1}\begin{pmatrix} \alpha
\beta \end{pmatrix}) $$

  • 一般的一一映射 ->利用 Jacobi Matirx 衡量变化
    6b0221290d050cdd2615a604da693d7.png
  • 多对一：考虑所有满足情况的原像的求和

相关系数与协方差

00511536afa90326b8592a51c313943.png

$$ \begin{align} & \text{Cov}(X,Y) = E[XY]-E[X]E[Y]
& E[XY] = \int \int uvF_{X,Y}(u,v)dudv \end{align} $$

  • 无关定义：

$$ \begin{align} & \text{Cov}(X,Y) = 0 (\rho_{X,Y}=0)\to \text{Uncorrelated}
& \text{Cov}(X,Y) > 0 (\rho_{X,Y}>0)\to \text{Positively Correlated}
& \text{Cov}(X,Y) < 0 (\rho_{X,Y}<0)\to \text{Negatively Correlated} \end{align} $$

  • 无关与独立关系
    1. 两变量独立时一定无关:

$$ \text{Cov}(X,Y) = E[XY]-E[X]E[Y] = E[X]E[Y]-E[X]E[Y] = 0 $$

  1. 两变量无关时不一定独立，独立性质比无关强
  2. 多变量无关只需考虑每一对之间相互无关即可，但是多变量相互独立需要考虑对于其组合的任意子集均满足独立的性质
    协方差性质: 线性，添加常数不改变

$$ Cov(aX+bY,cX+dY) = acVar(x)+bdVar(Y)+(ad+bc)Cov(X,Y) $$

$$ \rho_{aX+b,cY+d} = \rho_{X,Y} \text{ for } a,c >0 $$

相关系数的绝对值越接近 1，随机变量的线性相关性越强

应用

1. 随机变量的函数
考察随机变量经过映射后的分布情况
问题情境：已知一个随机变量 X 的概率分布，希望知道经过函数映射 $Y=F(X)$ 的概率分布
一般思路

  • 确定 X 与 Y 的支持集,可以先画 Y 关于 X 的函数图像，精准确定 Y 的定义域及其与对应 X 的值的对应关系，确定 Y 为离散型随机变量还是连续性随机变量
  • 可以通过画图确定，当 Y 对应小于某个值时对应 x 的精确取值范围区间，防止出错
    1. 对于连续性随机变量：
      首先寻找 Y 的 CDF:(注意关注需要考虑 c 可取哪些值)

$$ F_{Y}(c) = P{Y\leq c} = P{g(X)\leq c} $$

然后对 Y 的 CDF 进行微分即可得到对应的 pdf

  1. 对于离散型随机变量：
    直接计算：

$$ p_{Y}(v)=P{Y=v} = P{g(X)=v} = \int_{{u:g(u)=v}}f_{X}(u)du $$

逆函数
映射的函数为单调递增函数时，我们可以直接利用逆函数找到良好的对应关系

$$ \begin{align} & F_{Y}(c) = F_{X}(g^{-1}(c))
& f_{Y}(c) = f_{X}(g^{-1}(c)) \frac{1}{g^{‘}(g^{-1}(c))} \end{align} $$

生成满足特定分布的随机变量
问题情境
记 $F$ 为满足条件的 CDF 函数， $U$ 为在区间 $[0,1]$ 上均匀分布的随机变量，目的是找到一个函数 $g$ 使得 $F$ 为 $g(U)$ 的 CDF

解决：即为在均匀分布的随机变量上进行给定 CDF 函数的逆映射

  • 确定 $F$ 的逆函数

$$ F^{-1}(u) = min{c:F(c)\geq u} $$

  • 将 $F^{-1}$ 作为 $g$ 生成对应的分布

由 CDF 图像结合面积计算分布均值
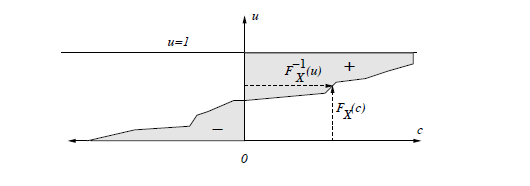
3b6eae34566b181832f2a29adfcfe41.png
左边阴影部分面积减右边

$$ \begin{align} & E[X] = \int_{0}^{\infty}(1-F_{X}(c))\, dc - \int_{-\infty}^{0} F_{X}(c) \, dc
& E[X] = \int_{0}^{1}F_{X}^{-1}(u)du \end{align} $$

2. 多随机变量和的分布
整值随机变量的和 ->卷积

$$ p_{S}(k) = P(X+Y=k) = \sum_{j}P_{X,Y}(j,k-j) $$

连续性联合随机变量的和
考虑先寻找 S=X+Y 的 CDF 再微分得到 PDF
CDF

$$ F_{S}(c) = P(S\leq c) = \int_{-\infty}^{\infty}(\int_{-\infty}^{c-u}f_{X,Y}(u,v)dv)du $$

PDF

$$ f_{S}(c) = \frac{dF_{S}(c)}{dc} = \int_{-\infty}^{\infty} \frac{d}{dc}\left( \int_{-\infty}^{c-u}f_{X,Y}(u,v)dv \right)du = \int_{-\infty}^{\infty}f_{X,Y}(u,c-u)du $$

Example4.6.5: ML Estimator，关注如何建模多维联合 pdf，同时进行获得 ML estimator
de108e4a4d31aebc76239b0a573531c.png a3d8c62d6a61ace1e52eb6460c73059.png
Example4: max 函数

$$ \begin{align} & F_{W}(t) = P(max(X,Y)\leq t)=P(X\leq t)P(Y\leq t)=F_{X}(t)F_{Y}(t)
& f_{W}(t)=f_{X}(t)F_{Y}(t)+f_{Y}(t)F_{X}(t) \end{align} $$

3. MMSE Estimation

$$ MSE = E[(y-\delta)^{2}] = \int_{-\infty}^{\infty}(y-\delta)^{2}f_{Y} \, dy $$

  • 常数估计
    当 $\delta = E[Y]$ 时，我们有 MSE 最小值为 $Var(Y)$
    即估计的常数对应随机变量分布的均值，相应的 MSE 为其对应的方差
  • 无约束估计

[!tip] 结论
对于非限制在给定观测结果 $X$ 的情况下估计随机变量 $Y$ 的分布，我们基于常数估计量以及 conditional pdf 推导出

  • $E[Y X]=g^{}(X)$ 其中 $g^{}(u)=E[Y X=u]$
  • 对应的 MSE 最小值为 $E[(Y-E[Y X])^{2}]=E[Y^{2}]-E[(E[Y X])^{2}]$

先根据联合概率分布 $f_{X,Y}$ 计算 $f_{X}$ 与 $f_{Y|X}$
再对每一个给定的 $u$ ，确定 $g^{*}(u)$ , 即利用积分计算条件期望
然后计算每一个给定的 u 对应的 MSE 再乘上相对应的 $f_{X}(u)$ ，积分得到最终结果

  • 线性估计
    根据逐步优化的结果，我们有给 $Y$ 的线性近似 $aX+b$
    当

$$ a = \frac{\text{Cov}(Y,X)}{\text{Var}(X)}， b = \mu_{Y}-a\mu_{X} $$

时，我们有 MSE 最小，此时

$$ \begin{align} & L(X) = \hat{E}[Y|X] = \mu_{Y}+ \frac{\text{Cov}(Y,X)}{\text{Var}(X)}(X-\mu_{X}) = \mu_{Y} + \sigma_{Y}\rho_{X,Y} \left( \frac{X-\mu_{X}}{\sigma_{X}} \right)
& MSE = \sigma_{Y}^{2}-\frac{(\text{Cov}(X,Y))^{2}}{\text{Var}(X)} = \sigma_{Y}^{2}(1-\rho ^{2}_{X,Y}) = E[Y^{2}] - E[\hat{E}[Y|X]^{2}] \end{align} $$

4. 联合高斯随机分布
联合高斯分布随机变量 ->对于这些随机变量的线性组合满足高斯分布
15534014eb9d176ba8e06a488371b89.png 405944df000a08b79256eaabe4cba4d.png

acde56f27824dff9e14f306edce8a95.png

9b7521b0b8ab13ba993482c3e3b8471.pngf60c3b914527a327f53e501428567df.png