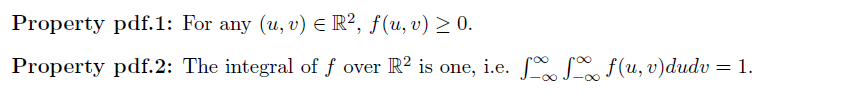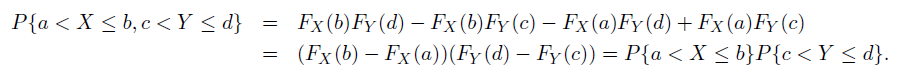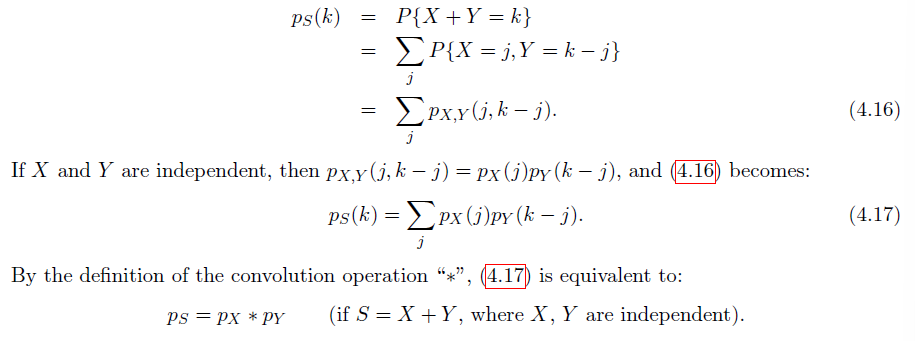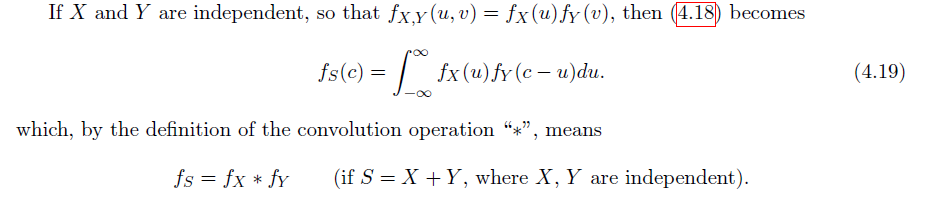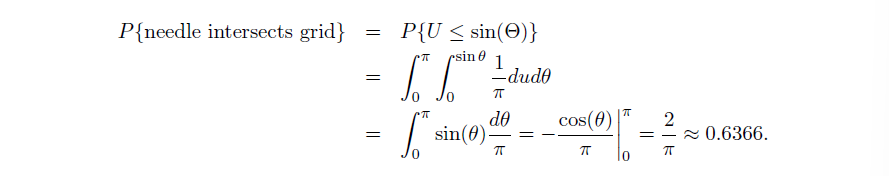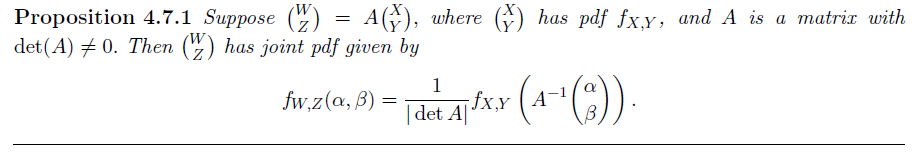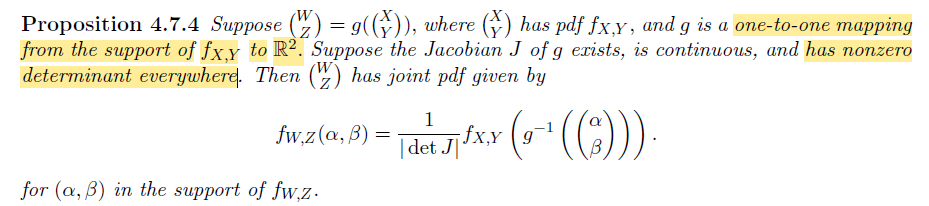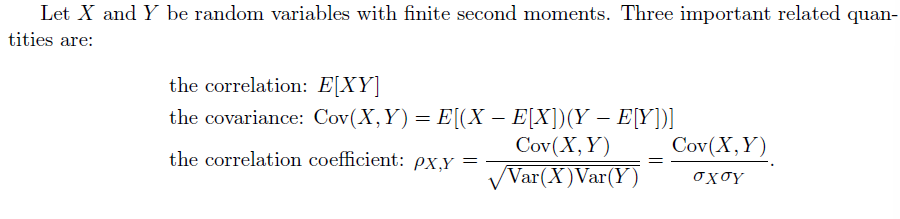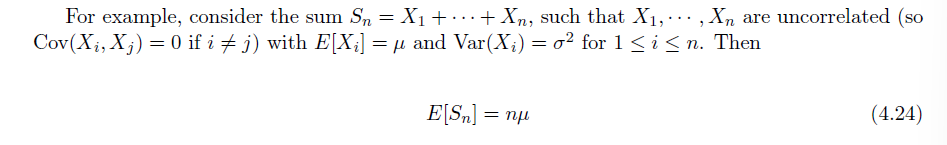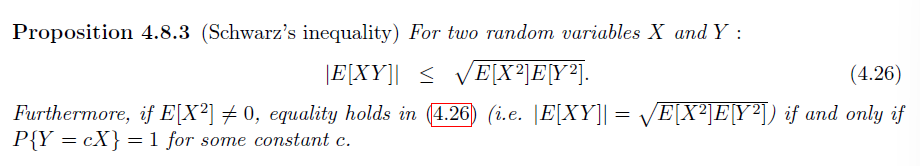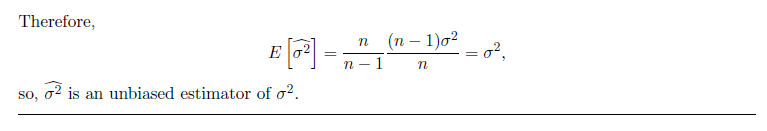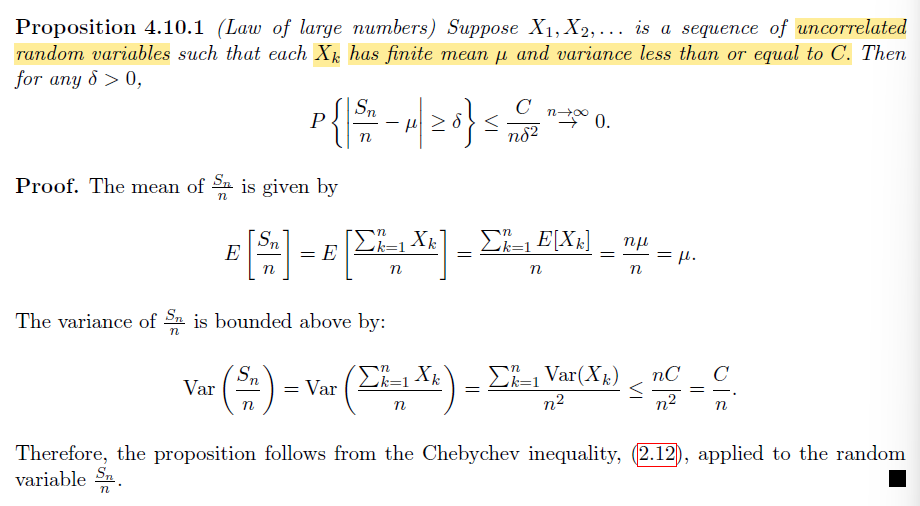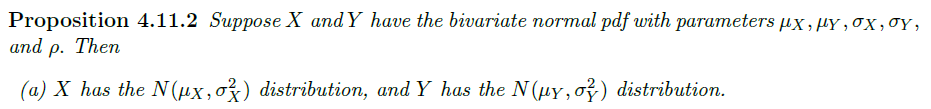Jointly Distributed Random Variables
#ECE313
Basic
Joint Cumulative Distribution Functions
Definition
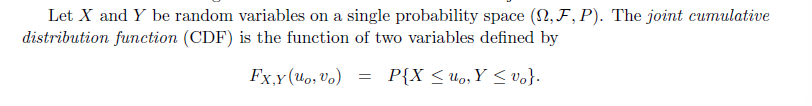
利用图像定义,我们有:
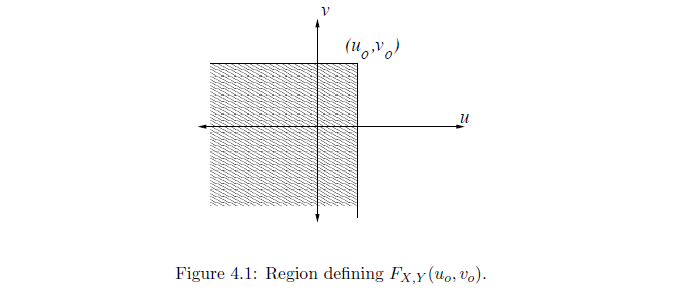
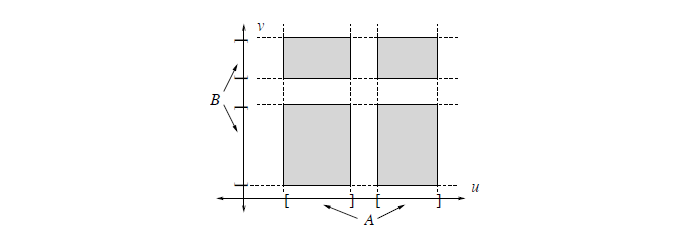
对于分布在一个区域内的联合概率分布,我们有:

Proposition
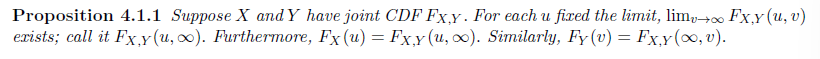
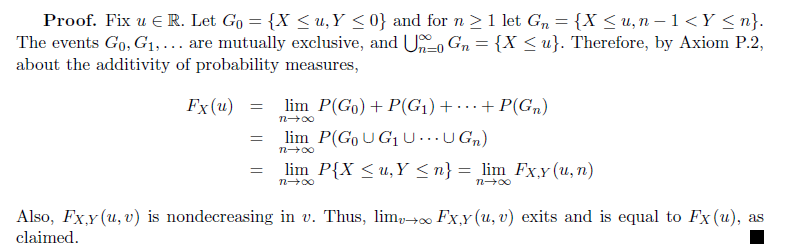
Properties

Joint Probability Mass Functions & Density Functions
离散型随机变量 ->Joint Probability Mass Functions
考虑在同一个概率空间中的离散型随机变量
同时结合全概率定理,我们可以由联合概率质量函数导出分别的概率质量函数
这等价于
在这种情况下
连续型随机变量 -Joint Probability Density Function
对于分布在同一个概率空间中的连续性随机变量
对于具体区域
Marginal pdfs:
Conditional pdf:
- 期望
同时还有
注意
Independence of random variables
Definition of independence for two random variables
Determining independence from pdf
X,Y 相互独立等价于:
为后续命题先补充相关概念:
-
Swap Property
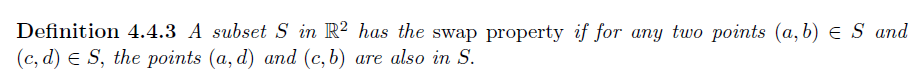
-
Swap Property 于 Product set 的等价性
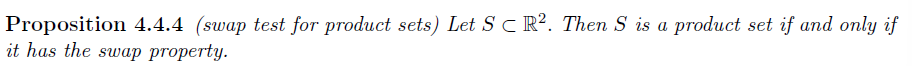
以下两个命题可用来判断自由变量是否随机分布(不一定充要)
Proposition1: 从条件概率角度出发研究变量独立性,考察 conditional pdf 是否仅与单变量有关

Proposition2:X,Y 为相互独立的联合分布连续随机变量,则

推论:当

Distribution of sums of random variables
Sums of integer-valued random variables
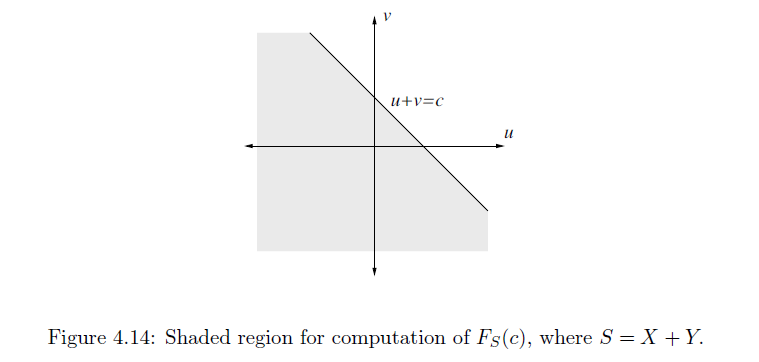
Sums of jointly continuous-type random variables
考虑先寻找
CDF
Example: 两满足正态分布的随机变量相加 ->考虑配方
Example2:Buffon Needle Problem

Example4.6.5: ML Estimator,关注如何建模多维联合 pdf,同时进行获得 ML estimator


Joint pdfs of functions of random variables
Transformation of pdfs under a linear mapping
考虑对原有随机变量做线性变换得到新随机变量
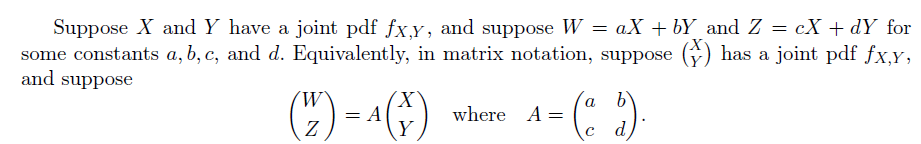
基于线性变换
记变换前后联合随机变量定义域所对应的区域分别为
理解:通过除以面积拉伸的系数实现概率密度的对应关系
Transformation of pdfs under a one-to-one mapping
对于一般的映射
我们可以猜想:
- 一一映射
- 注意求解映射后的支撑集(考虑映射后对应的随机变量的范围限制)
Transformation of pdfs under a many-to-one mapping
当定义的函数映射存在多对一的情况是,我们修改命题 4.7.4,将映射后的联合随机变量分布修改为对满足条件的原联合随机变量分布的求和
Correlation and Covariance
Basic Concept
对于联合随机变量分布,我们考虑类比单随机变量分布的情况引入类似均值与方差的定义
- Correlation 相关
- Covariance 协方差
- Correlation Coefficient 相关系数
简便计算协方差公式:
其中
协方差&相关:
- 无关定义:
-
无关与独立关系
- 两变量独立时一定无关:
- 两变量无关时不一定独立,独立性质比无关强
- 多变量无关只需考虑每一对之间相互无关即可,但是多变量相互独立需要考虑对于其组合的任意子集均满足独立的性质
- 当 X 或 Y 均值为 0 时,我们有
-
协方差性质
- 协方差对于其两元素均满足线性
- 对随机变量增加常数不改变协方差
- 当两变量无关时,其和对应随机变量的方差等于各自方差之和
-
相关系数
相关系数本质上为经过标准化的协方差,没有单位与维度,对随机变量进行线性或仿射变换不会改变相关系数
Property
推论:
Example
注意表示 Sample Mean 与 Sample Variance 时常常用
Minimum Mean Square Error Estimation
Constant Estimators
情境建模:
对于一个已知分布随机变量 Y,我们利用一个常数
经过配方,我们容易将 MSE 化简为与
当
即估计的常数对应随机变量分布的均值,相应的 MSE 为其对应的方差
Unconstrained Estimators
情境建模:
希望基于随机变量
注意利用条件概率公式化简(固定某一个 u,符合我们在确定观测 X 的情况下估计 Y)
[!tip] 结论
对于非限制在给定观测结果的情况下估计随机变量 的分布,我们基于常数估计量以及 conditional pdf 推导出
$E[Y X]=g^{}(X) g^{}(u)=E[Y X=u]$
对应的 MSE 最小值为 $E[(Y-E[Y X])^{2}]=E[Y^{2}]-E[(E[Y X])^{2}]$ 先根据联合概率分布
计算 与
再对每一个给定的,确定 , 即利用积分计算条件期望
然后计算每一个给定的 u 对应的 MSE 再乘上相对应的,积分得到最终结果
Linear Estimators
情境建模
考虑将用观测结果
此时 MSE 为:
我们可以考虑采取分别求偏导或者累次优化的方式寻找 MSE 最小时对应的
根据逐步优化的结果,我们有给
当
时,我们有 MSE 最小,此时
其中使得 MSE 最小的线性估计
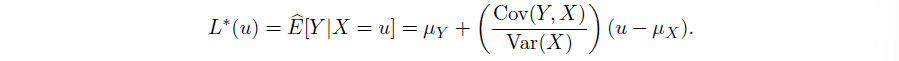
我们发现当 X,Y 线性相关程度越高(即
三种方法估计的比较 ->假设越宽泛,优化得到的 MSE 越小
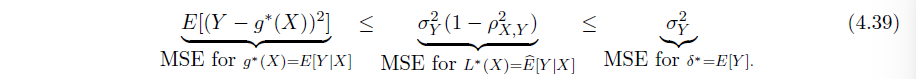
重点关注 Example 4.9.2
Law of Large Number and Central Limit Theorem
- 大数定理 ->用常数估计多个随机变量的和
- 中心极限定理 ->用高斯分布估计多个随机变量的和
Law of Large Numbers(LLN)
LLN 建模基于的情境:
给定一系列均值相同的独立(或弱相关的)的随机变量,同时对随机变量的规模有一定要求,LLN 认为当随机变量个数趋于无穷时,他们和的均值收敛于一个定值
Central Limit Theorem
中心极限定理:
认为多个独立相同分布的随机变量(均值与方差均有限),他们和的分布标准化后趋于高斯分布
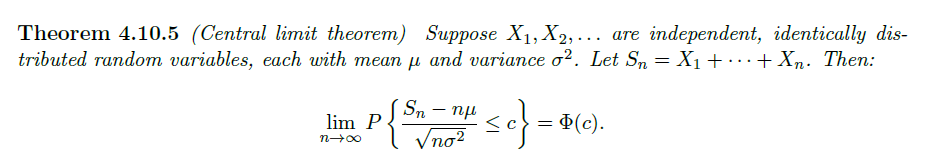
注意有时需要对高斯近似用 Continuity Correction
Joint Gaussian Distribution
联合高斯分布随机变量 ->对于这些随机变量的线性组合满足高斯分布


判别两变量是否符合高斯联合随机分布的另一种方法 ->研究其 pdf 是否为关于两变量的符合条件的指数上二次多项式 (bivariate normal pdf)(非退化的情况)

From the standard 2-d normal to the general
先研究标准双变量正态分布的情况 ->再通过线性变换(变换方差与相关系数)以及平移(改变均值)得到一般形式

Key properties of the bivariate normal distribution
- 利用 X 估计 Y 时,使 MSE 最小的估计函数为线性的
-
**给定 X 关于 Y 的分布为条件概率分布为正态分布 $N(\hat{E}[Y X=u],\sigma_{e}^{2})$**,注意与上述 Linear Estimator 相关联(见 Homework13 5)