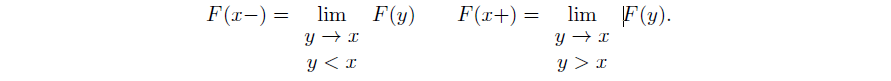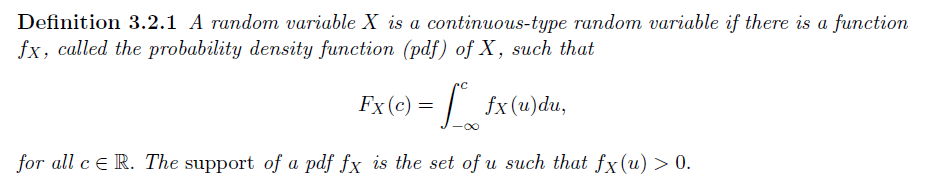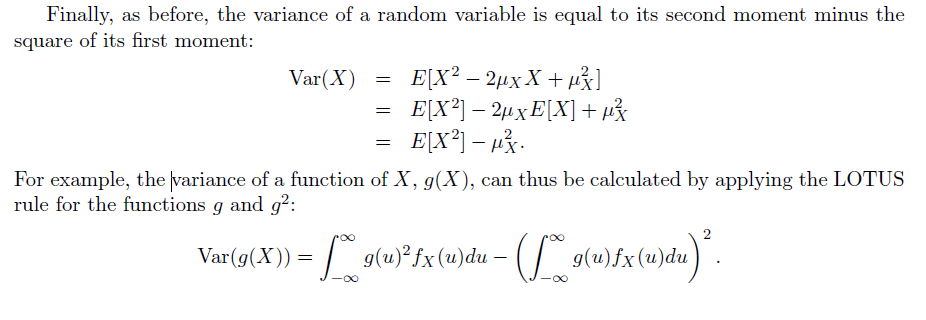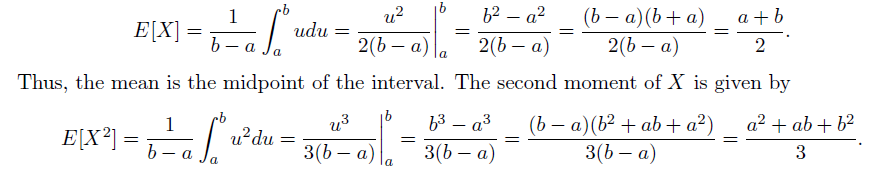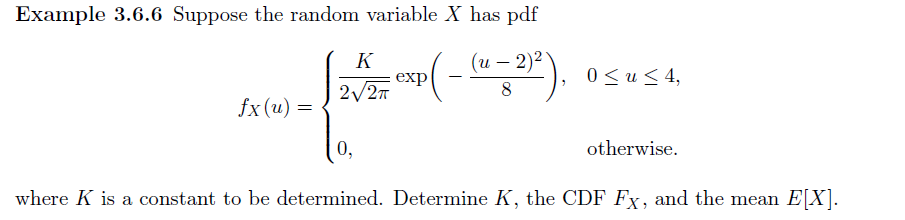#ECE313

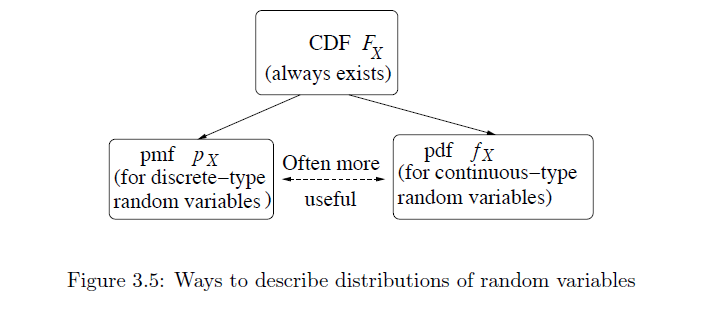
Cumulative distribution functions

Basic

  • Definition
    To be on mathematically firm ground, random variables are also required to have the property that sets of the form ${\omega :X(\omega)\leq c}$ should be events-meaning that they should be in F: Since a probability measure P assigns a probability to every event, every random variable X has a cumulative distribution function (CDF), denoted by
    $F_{X}$

$$ F_{X}(c) = P{\omega:X(\omega)\leq c} = P{X\leq c} $$

CDF 用来表示随机变量分布在一定区间内的累积概率

极限与差分记号：
9fd7238706ecede182b8210a0acf588.png

$$ \Delta F_{X}(x)=F_{X}(x)-F_{X}(x-) $$

接下来我们给出如何确定 $P{X<c}$ 与 $P{X \in (a,b]}$ 与 $P{X=c}$
6af1c94ba43617d8b1fc03bd33176bc.png

6024729ab6cbc22de61ee98c1a8f753.png

我们容易观察到: 当 $F_{X}$ 在 c 取值连续时，我们均有 $F_{X}(c)=0$

  • Property
    函数 F 能作为随机变量的累计分布函数的条件
    7e11e0df7a189660ece6c88993c9821.png

Continuous & Discrete Random Variables

3f4db407a80066a8e59508f83a31350.png

  • 离散型
    随机变量的取值集合为有限集或可数无限集

$$ \begin{align} & \text{pmf: } p_{X}(u)=P{X=u}
& \text{CDF: } F_{X}(c)=\sum_{u:u\leq c}p_{X}(u) \end{align} $$

  • 连续性：定义为概率密度函数的积分
    400b3415fe3c504bd1b084bd8e4a4d6.png

Continuous-type Random Variables

  • Definition
    42f6f1ab65ef5984ab6a80b39c8c957.png
    注意：
    当随机变量连续且其概率密度函数也连续时，我们有 CDF 可微
    直接对 CDF 求导得到 PDF

  • Property
    对于连续的 pdf，我们并不关注孤立点的取值（因为取值永远为 0）
    6eea97eb456b0406a3e626a8d5279cb.png

  • 均值与方差
    613ddbfada720cf80b6f08d7693e367.png

2e93063d16bae55d5155cf4c124aa79.png

Distribution

Uniform Distribution(均匀分布)

  • Definition
    cf3295097d29aa47940b3f66f6e3cdb.png

  • 均值与方差
    cb22bdf028daaa7cbf4bf5fb2a47151.png
    a86cb746dbfb33ea24ba0d8a0fb57d7.png

Exponential Distribution

Definition
38e746f4c650503be6b926957f23eec.png

  • 均值与方差
    b946f660acf0e53b8b409a92810d921.png

  • Property
    9fa7615a2879c18f693b56a86b28a95.png
    与几何分布的联系
    Exponential Distribution 为几何分布在连续时取极限的情况
    其中 $\lambda$ 可以理解为失败概率

274e1fee50ab8dce200347940f4c3ed.png

Poisson Processes

Intro

Exponential random variables are limits of scaled geometric random variables->Poisson Processes are limits of scaled Bernoulli processes
指数分布本质上为几何分布的极限
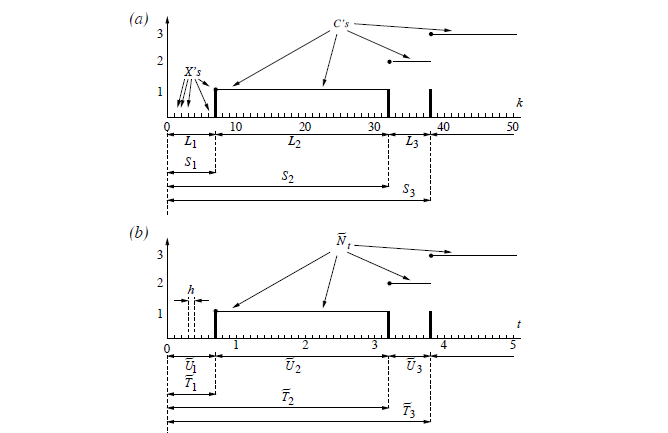
87c1d11aae810b21f2214751840866c.png
58fe62f87659366162f8a6c38db8152.png

  • $U_{j}$ 前 $j-1$ 次 count 与 $j$ 次 count 之间的时间间隔，服从 exponential distribution,参数为 $\lambda=\frac{p}{h}$
  • $N_{t}$ 时间为 t 时出现的 count 次数，服从于二项分布，近似为泊松分布，均值为 $\lambda t$

Definition and Properties

核心即为将一个离散的不断进行伯努利实验的过程用时间变量描述为连续的过程
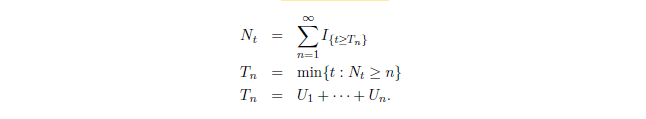
b3e0921341f9f2c26772816619f53b1.png

  • $N_{t}$ 给定 t,关注在之前的时间内出现了几次 count,利用判别 $I$ 来表示
  • $T_{n}$ 记录出现 n 次 count 时所用的最小时间
  • $U_{n}$ 第 n-1 次 count 与第 n 次 count 之间的时间间隔

c156a6991400598cc45ce847171b8e6.png
8f91c7c7d4fd5955b55aff601f4274a.png
ef67a7f534234e296c310429a44b9c2.png
在很多情况下将时间划为不交的并集可以充分利用其相互独立性

Example:
df4340da72680102e28988e9ba6ddfd.png
409880ff488f432970512fca3f419cf.png

Erlang Distribution(埃尔朗分布)

bf02d7c2af628ffb2954708942a0601.png
rth count 所经过的时间服从 Erlang Distribution，理解为 r 个独立随机过程的加和

$$ \begin{align} E(T_{r}) = \frac{r}{\lambda}
Var(T_{r}) = \frac{r}{\lambda ^{2}} \end{align} $$

Linear Scaling of PDFs and the Gaussian Distribution

Scaling Rule for pdfs

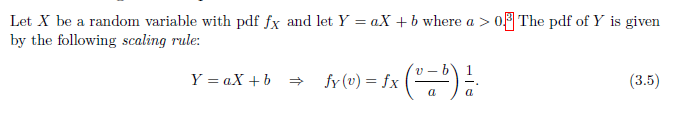
f4dd7cf6b568ff2688e3b111ec6a3be.png
通过分析拉伸平移前后对应变量分布的概率来推导
0bb92309104854ca4620d77b1777001.png
平移不改变总体形态，如果涉及伸缩注意纵轴上相应的变化

Gaussian Distribution 正态分布

Definition
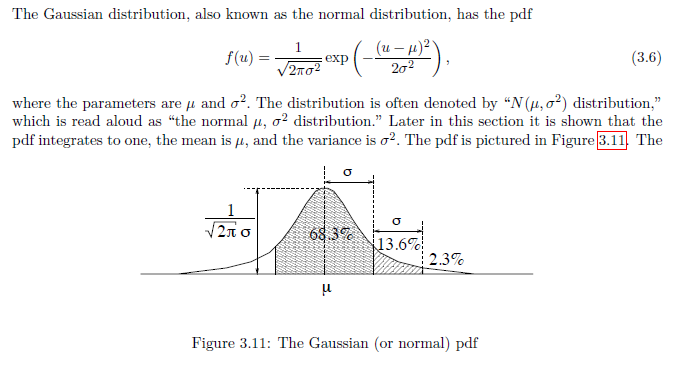
a325e4b2a31c7aba9856bea54ca8332.png
注意不同 $\sigma$ 对应的分布概率
68.3 -> 95.5 -> 99.7
Standard Normal Distribution
b9a4740728451069b874d814007b7c4.png

注意常用的函数:
同时还关注到正态分布的 pdf 为偶函数

  • $\Phi(u)$ 表示对于标准正态分布从负无穷积到 u 的概率
  • $Q(u)$ 表示对于标准正态分布从 u 积到正无穷的概率

$$ Q(u) = 1 - \Phi(u) = \Phi(-u) $$

Linear Scaling
只需要考察标准正态分布的情况，其余的情况都可以通过 Linear Scaling 实现，关注 scaling law 即可

$$ \begin{align} & X \sim N(0,1)
& Y = \sigma X + \mu
& Y \sim N(\mu, \sigma) \end{align} $$

4f3a2edcab6289edb49dfa8edcd2c90.png

证明正态分布积分为 1（利用极坐标）
9c5ddf9dc6bd2bf79c20012f33ceffb.png
进一步利用分部积分证明方差为 1
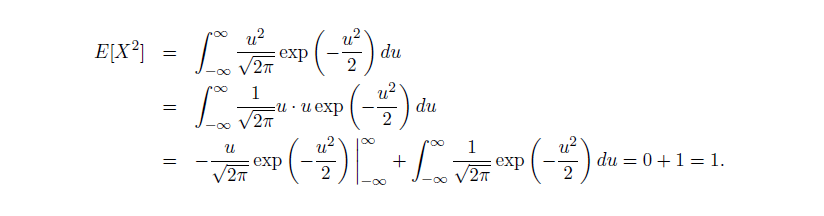
b60780db0bad21b8c6d74fba83dd292.png

当计算非标准正态分布的概率时，常常通过 Linear Scaling 返回到标准正态函数利用 $\Phi$ 或者 $Q$ 计算

$$ \begin{align} & P(Y \leq u) = P\left( \frac{Y-\mu}{\sigma} \leq \frac{u-\mu}{\sigma} \right) = \Phi\left( \frac{u-\mu}{\sigma} \right)
& P(Y > u) = 1 - \Phi\left( \frac{u-\mu}{\sigma} \right) \end{align} $$

Example:
5ac96bf5bb558e728586550bdc8476f.png
eb89714ff441de34d0ac54960cc71a2.png

Central Limit Theorem and the Gaussian Approximation

CLT：中心极限定理的核心思想：
当多个独立随机变量相加，且单个随机变量值相比总和的量级较小，那么他们的和可以近似为正态分布
51abb622eda56205393fcc4e4c29c5d.png
Central Limit Law
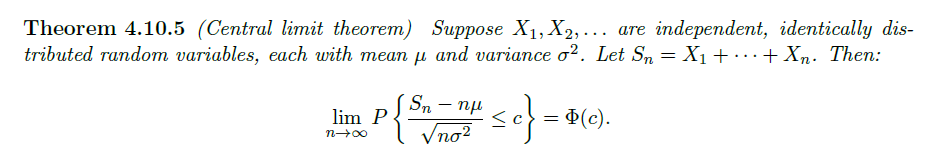
ff2e3790a30bffddefbf18498b67d82.png

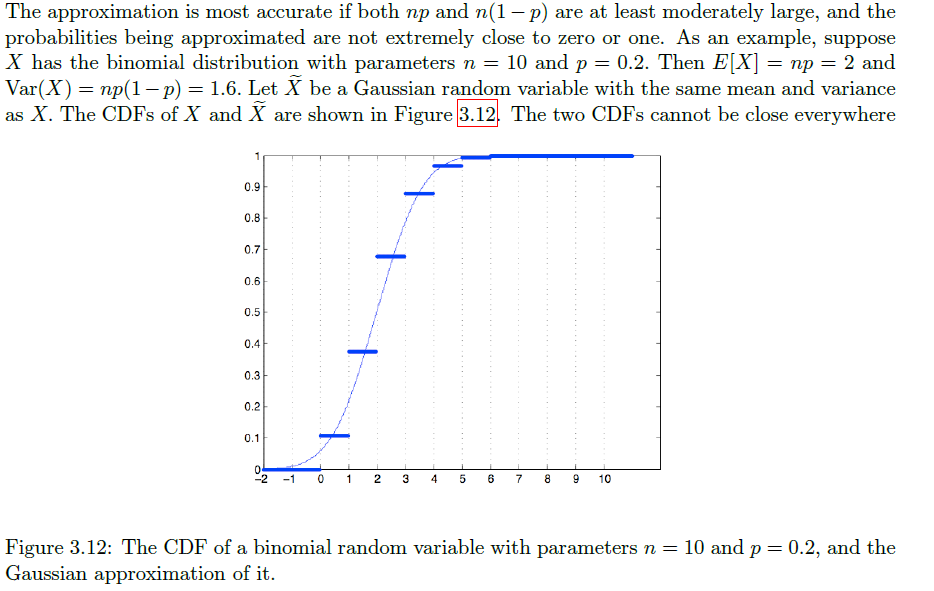
应用 1：利用 CLT 近似二项分布（因为其可以表示为多个伯努利分布的和）
根据二项分布的参数 $n,p$ 计算出分布的均值与方差作为近似正态分布的均值与方差在 $np$ 与 $n(1-p)$ 相对较大时近似较精确

a01d8d72ea5a8438b7d5adafcf1e2ec.png

当我们利用正态分布估计离散变量的概率分布时，需要进行 continuity correction
我们发现，利用两个连续整数的中间值进行估计较为精确（当 X 为取值整数的随机变量时）
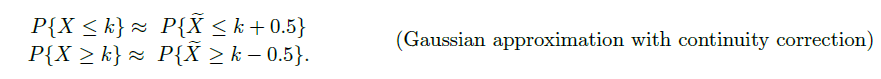
44f4b6d2e0ab4d05886d135cbb0aec4.png
利用考虑下式进行记忆

$$ P(X=k) \approx \int_{k-0.5}^{k+0.5}f_{X}(u)du $$

Theorem: DeMoivre-Laplace Limit Theorem（利用正态分布对二项分布的极限近似）
f2b543ec2f844ed14c600f5e2d7d6cc.png

ML Parameter Estimation for Continuous-Type Variables

对于现实情境进行概率建模时，我们常常需要考虑选取合适的参数作为选取随机变量分布的参数，对于连续型随机变量而言，我们依然考虑选取能使对应采样结果最大所对应的参数，其中对应采样结果的参数概率通过在临近区间内积分确定

$$ f_{\theta}(u) \approx \frac{1}{\epsilon}P\left{ u-\frac{\epsilon}{2} < X < u + \frac{\epsilon}{2} \right} $$

参数 $\theta$ 基于观测结果 $u$ 的最大似然估计记为 $\hat{\theta_{ML}(u)}$, 该参数能最大化 $f_{\theta}(u)$

Functions of a random variable

The distribution of a function of a random variable

问题情境：已知一个随机变量 X 的概率分布，希望知道经过函数映射 $Y=F(X)$ 的概率分布

一般思路

  • 确定 X 与 Y 的支持集,可以先画 Y 关于 X 的函数图像，精准确定 Y 的定义域及其与对应 X 的值的对应关系，确定 Y 为离散型随机变量还是连续性随机变量
  • 可以通过画图确定，当 Y 对应小于某个值时对应 x 的精确取值范围区间，防止出错
    1. 对于连续性随机变量：
      首先寻找 Y 的 CDF:(注意关注需要考虑 c 可取哪些值)

$$ F_{Y}(c) = P{Y\leq c} = P{g(X)\leq c} $$

然后对 Y 的 CDF 进行微分即可得到对应的 pdf

  1. 对于离散型随机变量：
    直接计算：

$$ p_{Y}(v)=P{Y=v} = P{g(X)=v} = \int_{{u:g(u)=v}}f_{X}(u)du $$

求解对应的方差与均值
可以考虑直接用 LOTUS

重要等式:(考虑分部积分和递推)

$$ \int_{0}^{\infty}u^{n}e^{-u}du = n! $$

Example
dd12cb254bb80d046a16e91c5b6e4fc.png

534ab8765a349bb594989d6391288e8.png

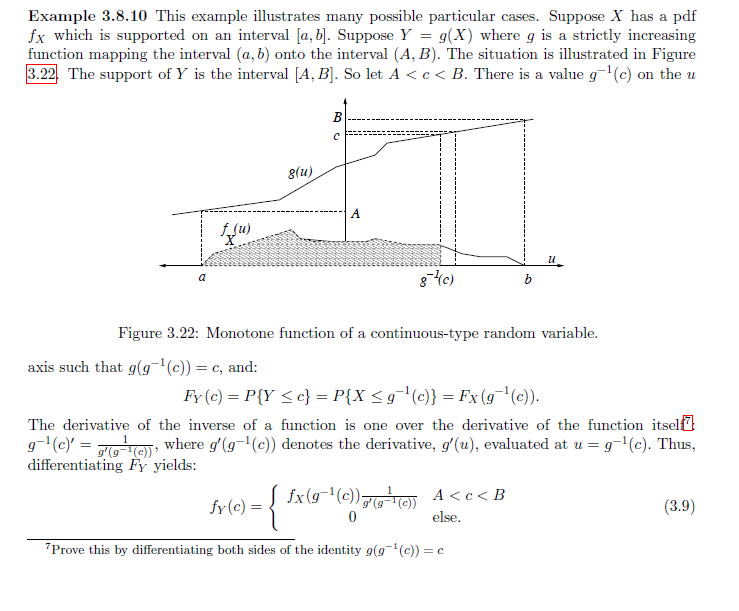
e39fa26c4e45d364bd5acac2cca26c2.png
当映射的函数为单调递增函数时，我们可以直接利用逆函数找到良好的对应关系
核心：

$$ F_{Y}(c) = F_{X}(g^{-1}(c)) $$

988ce2af27cd79d2ac402fce2a2414a.png

将随机变量的 CDF 添加到本身 ->实现一个均匀分布

Generating a random variable with a specified distribution

问题情境
记 $F$ 为满足条件的 CDF 函数， $U$ 为在区间 $[0,1]$ 上均匀分布的随机变量，目的是找到一个函数 $g$ 使得 $F$ 为 $g(U)$ 的 CDF

解决

  • 确定 $F$ 的逆函数

$$ F^{-1}(u) = min{c:F(c)\geq u} $$

  • 将 $F^{-1}$ 作为 $g$ 生成对应的分布

The area rule for expectation based on the CDF

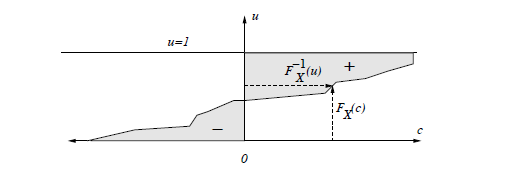
3b6eae34566b181832f2a29adfcfe41.png
由 CDF 图像结合面积简单地计算分布的均值: 即为上图右侧的阴影面积减左侧的阴影面积

$$ E[X] = \int_{0}^{\infty}(1-F_{X}(c))\, dc - \int_{-\infty}^{0} F_{X}(c) \, dc $$

考虑从 u 轴上积分，我们有:

$$ E[X] = \int_{0}^{1}F_{X}^{-1}(u)du $$

证明：
c13d85ac8b1cb7f41b1164ebbfe8b13.png

Binary Hypothesis testing with continuous-type observation

问题背景:

  • 考察连续性随机变量的分布
  • 两种假设 $H_{1},H_{2}$ 假设正确时对应不同的 pdf $p_{1},p_{2}$
  • 基于实际观测情况确定假设

Term:

  • Likelihood Ratio:

$$ \Lambda(u) = \frac{f_{1}(u)}{f_{2}(u)} $$

  • Likelihood Ratio Test:

$$ \begin{align} & \Lambda > \tau, \text{declare H1 is true}
& \Lambda < \tau, \text{delcare H0 is true} \end{align} $$

ML Likelihood: 对应的 $\tau=1$
MAP Likelihood: 对应的 $\tau=\frac{\pi_{0}}{\pi_{1}}$

  • P
    求概率时即在对应的 X 的区间范围内考虑 pdf 的积分或者计算面积
    2ff7224f979a1e06888ce712a2417ab.png