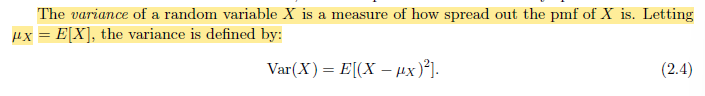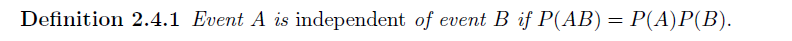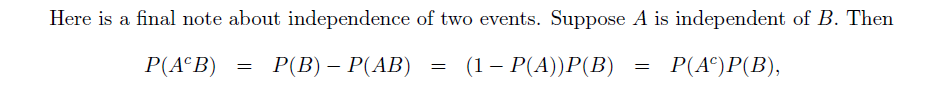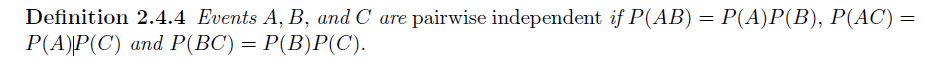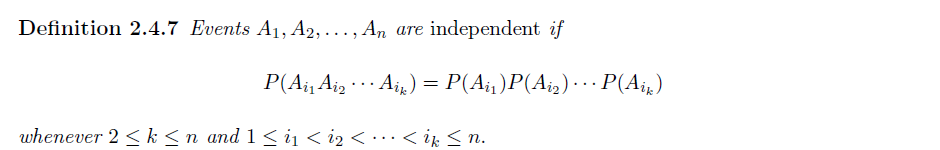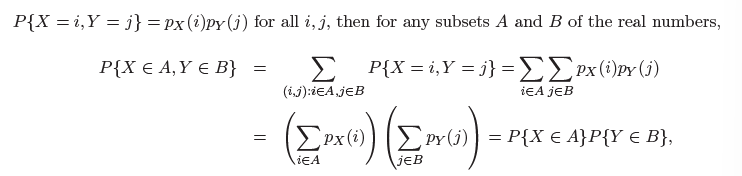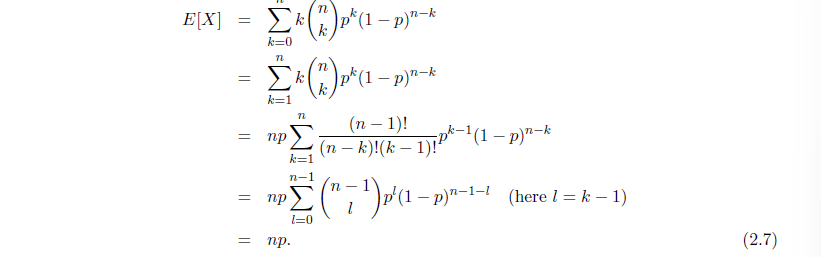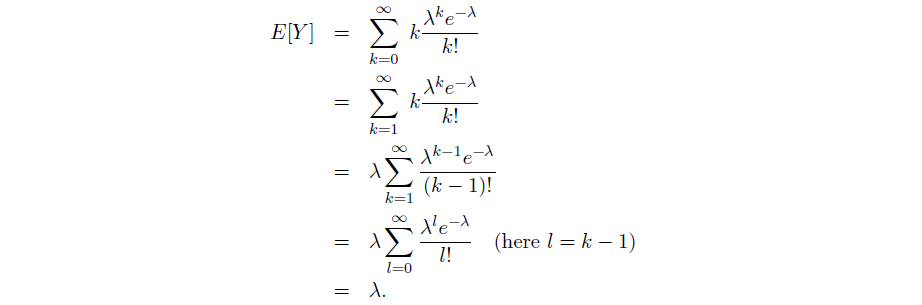#ECE313

Random variables and probability mass functions

Definition

离散型随机变量
A random variable is a real-valued function on $\Omega$
900c218561b0bebebf5a03aecec38b8.png
对于每次实验，我们都可从样本空间中确定一个结果 $\omega$ ,并决定对应的 $X(\omega)$ 。给定一个子集，我们即可确定对应的 $X(\omega)$ 以及所对应的 $\omega$ ,进而确定由该子集决定的事件的概率

概率密度函数

Probability Mass Function
0a5ff1bb81abbf5eabad55d68759adc.png
即对应随机变量取值的概率

均值（期望）与方差

Mean

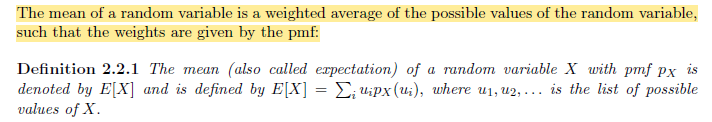
99500ed5673340dfaf5a9c38da7eb12.png
当涉及到与定义的随机变量有关的函数的均值时，我们可以直接取对应的概率求均值 ->Law of the Unconscious Statistication
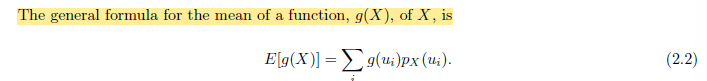
f3b89e074a5b86a044a4f72423a86ff.png
期望的重要性质 ->线性
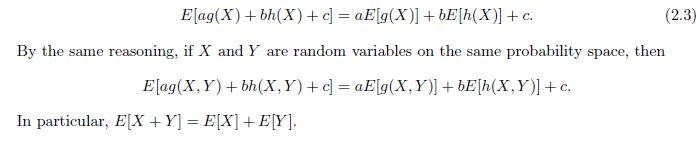
13fb08d3a8bfd93ff1216ba1247db82.png

Variance

933e09f4c74217ac54b8dc9e7dcf6b3.png
用于衡量随机变量取值的分布情况

Standard Deviation: $\sigma_{X}=\sqrt{ Var(X) }$

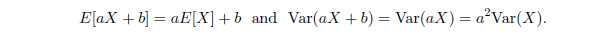
bc6010db1252ddf69152a67bef414fe.png
Application: Standardized Version of Random Variable
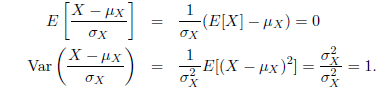
ac97e8e6bc7167ed2430cb20e100c34.png

Conditional Probability

Basic

  • Concept
    1950b7ad878f439965b84540c30594c.png
  • Property
    d4d5b41c21c16b4e14d0bbfaa32e176.png

Independence

  • Definition
    多事件相互独立需要对齐任意子集事件的组合均满足独立条件
    bcb376fc97e304c6943166c862f7555.png
    b94c91ad11a7c919c2162bb3a322274.png
    823d005ec445836a7e3a9dc7d308056.png
    fcda6b1fc05689d84a715020326804d.png
    b7842eb7dbccac649ac2ab0d1ad9d1f.png

Independent Random Variables

  • Definition
    两离散随机变量相互独立当且仅当其所对应所有取值的事件组相互独立

554da6f26a652692655c1af78a147d5.png
56d420082916697eb517400c35d398d.png

同理，对于多个离散型随机变量相互独立的情况，需要其所对应的所有事件组相互独立

Distribution

Bernoulli distribution

Definition
伯努利分布即为两点分布，随机变量的取值仅有 0 和 1，1 对应的取值为概率 p
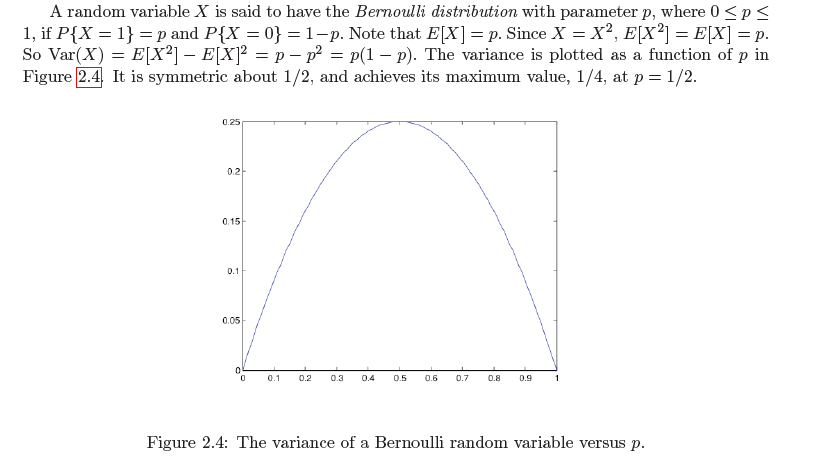
59aca718c518494acf19a9047675347.png

Binomial Distribution

Definition
重复 n 次独立的伯努利实验，以 1 出现的次数作为随机变量的取值
6b9220ad96f3d4218bc7744ca80e4f2.png

注意到我们有：

$$ \sum_{k=0}^{n} \begin{pmatrix} n
k \end{pmatrix} p^{k}(1-p)^{n-k} =1 $$

Mean
4af75baa69c61e179d95af6b0927272.png
Variance

$$ Var(X) = np(1-p) $$

最大概率的 k
利用中间项分别大于前项、后项求解

Geometric Distribution

Definition
进行一系列伯努利实验，记 $p_{L}(k)$ 为首次出现 1 进行的实验次数
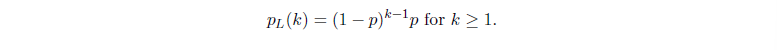
c3c80330b258a2e90e4bc0044652574.png
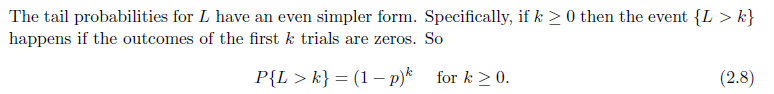
3e20a7ed876a91f0a4b653726640b77.png
注意 Tail Provability 的便捷计算，直接考虑之前全部失败即可
注意到，我们有：

$$ \sum_{k=1}^{\infty}(1-p)^{k-1}p=1 $$

Mean

$$ E(L)=\frac{1}{p} $$

考虑差比数列或者母函数
便捷推导：

$$ E[L]=p + (1-p)E[L+1] $$

Variance

$$ Var(L)=\frac{1-p}{p ^{2}} $$

便捷推导：

$$ E[L^{2}]=p+(1-p)E[(L+1)^{2}] $$

Property
56676b2dc94797e395f848f6071fbe0.png
Meaning:
之前进行的实验次数与还要进行的实验次数无关
693267c45245424971a7acd6d6986c5.png

Interesting Example:2.5.1 将问题进行拆解，类推到作业 3 的第三题，考虑几次结果相互独立 (即为 Negative Bernoulli Distribution)

Bernoulli process and the negative binomial distribution

问题背景：考虑进行无限次伯努利实验，得到一个无穷数列表示每次实验的结果，记为 $X_i$,从此出发我们可以用以下四个数列分别描述整个伯努利过程以及采样路径

  • Underlying Bernoulli sequence $X_{i}$: 表示第 i 次实验的结果
  • 每观察到下一次成功实验所多需要进行的实验次数 $L_{i}$, 我们容易知道 $L_{i}$ 服从概率为 p 的几何分布
  • 进行 k 次实验后累计的成功实验的次数 $C_{k}$, 我们有

$$ C_{k} = \sum_{i=1}^{k}X_{i} $$

其中 $C_{l}-C_{k}$ 即表示了 $l-k$ 实验过程中成功实验的增量，其在不相交的区间上也是相互独立的

  • 得到 $j$ 个 1 所累积进行的实验次数 $S_{j}$，我们有 (注意问题情境 ->n 个 geometric distribuyion)

$$ S_{j} = \sum_{i=1}^{j}L_{j} $$

基于此，我们将 $S_{r}$ 所满足的概率分布记为 Negative Binomial Distribution, 参数为 r 与 p
PMF:
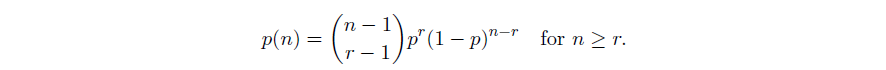
d1eab664f82ce86fb449be161cf481b.png
Mean:

$$ E[S_{r}] = rE[L_{1}] = \frac{r}{p} $$

Variance:

$$ Var(S_{r}) = rVar(L_{i}) = \frac{r(1-p)}{p ^{2}} $$

均可以利用母函数推导，类似几何分布（或者通过分解考虑变量之间的独立关系）
对于方差则需要考虑不同随机变量的 Correlation

Poisson Distribution - A limit of binomial distribution

Definition
0912eb64c3019ebaaabfe29b39c766e.png
考虑参数 $\lambda$ ,核心即为：

$$ p(k) = \frac{e^{-\lambda}\lambda ^{k}}{k!} $$

利用泊松分布对于 n 很大 p 很小的二项分布进行近似，以避免计算复杂的二项式系数
近似的原理：
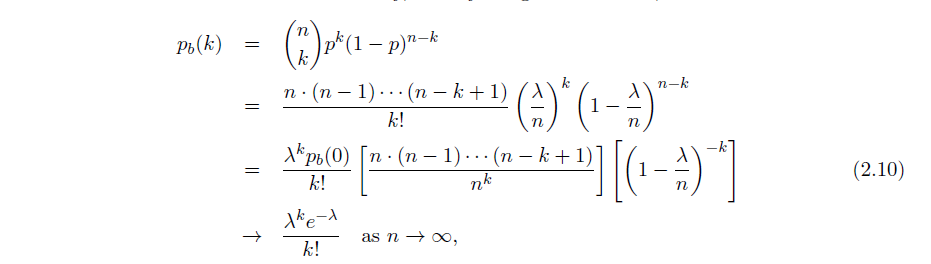
df38b8fdd839bc7b3d2d817fa23d675.png

Mean
efae726f11a5613edff161cf7b2ae8d.png
Variance

$$ Var(Y)= \lambda $$

也可对二项分布在 $n\to \infty$ 的时候取极限