Convolution, Impulse, Sampling, and Reconstruction

#ECE210

卷积 (Convolution)

卷积的概念

我们在之前的章节 (Ch 5-7) 学习了如何使用频率响应 $H(\omega )$ 来分析 LTI 系统的输出 $Y(\omega )=F(\omega )H(\omega )$ 。卷积提供了一种完全在 时域 (time domain) 中计算系统输出的方法。

给定两个信号 $f(t)$ (例如系统输入) 和 $h(t)$ (例如系统的冲激响应)，它们的卷积定义为一个新的信号 $y(t)$ :

$$y(t)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(\tau )h(t-\tau )d\tau$$

我们通常用星号 * 来表示卷积运算 :

$$y(t)=f(t)\ast h(t)$$

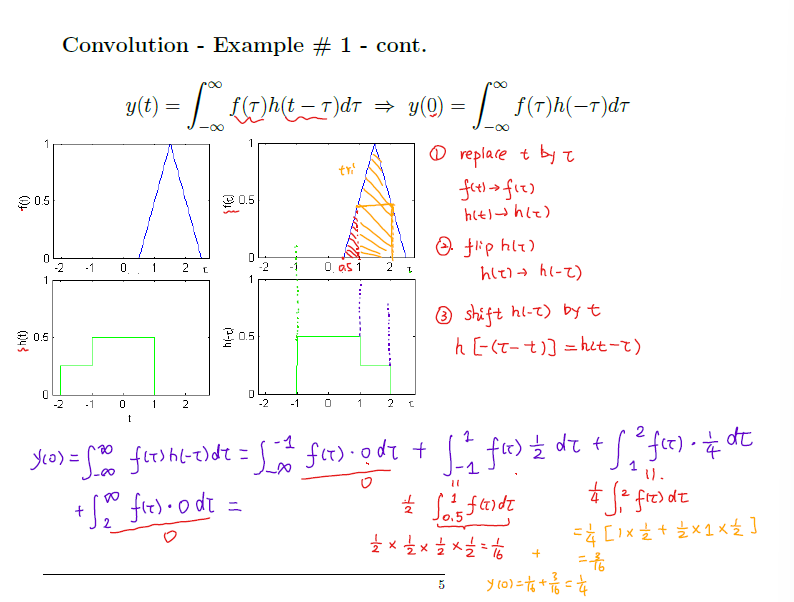
这个积分的意义是什么呢？ 我们可以把 $h(t-\tau )$ 看作是在时间 $t$ 处，系统对过去 ($\tau <t$) 和未来 ($\tau >t$，如果是非因果系统) 输入 $f(\tau )$ 的一种 加权叠加 (Weighted linear superposition)。$h(t-\tau )$ 本质上是 $h(\tau )$ 经过 翻转 (flip) 变成 $h(-\tau )$，再 平移 (shift) $t$ 个单位得到 $h(t-\tau )$

技术比喻: 想象 $h(-\tau )$ 是一个特定形状的“模板”或“权重窗口”。计算 $y(t)$ 时，我们将这个模板沿着时间轴 $\tau$ 滑动。在每一个位置 $t$，我们将模板 $h(t-\tau )$ 与输入信号 $f(\tau )$ 对齐，将两者对应点相乘，然后将所有乘积的结果积分 (求和)，得到该位置 $t$ 的输出值 $y(t)$。这个过程就像是用一个“加权平均”的窗口滑过输入信号。

卷积的计算

1. 图形法 (Graphical Method):
   1. 选择一个信号进行翻转和平移，通常选择形状更简单的那个，比如 $h(t)$ 变成 $h(t-\tau )$。步骤是：
      • 变量替换：$h(t)\to h(\tau )$。
      • 翻转：$h(\tau )\to h(-\tau )$。
      • 平移：$h(-\tau )\to h(t-\tau )$ (向右平移 $t$)。
   2. 将翻转平移后的信号 $h(t-\tau )$ 与另一个信号 $f(\tau )$ 相乘。
   3. 对乘积结果 $f(\tau )h(t-\tau )$ 关于 $\tau$ 从 $-\mathrm{\infty }$ 到 $\mathrm{\infty }$ 进行积分。
   4. 根据 $t$ 的不同取值范围，确定积分的上下限和结果表达式。

1. 利用卷积性质 (Using Properties): 有时利用卷积的性质可以简化计算。

卷积的性质

卷积有一些非常重要的性质：

1. 交换律 (Commutative): $f(t)\ast h(t)=h(t)\ast f(t)$ $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(\tau )h(t-\tau )d\tau ={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}h(\tau )f(t-\tau )d\tau$$ 这意味着谁做“模板”进行翻转平移，结果都一样。

2. 结合律 (Associative): $[f(t)\ast g(t)]\ast h(t)=f(t)\ast [g(t)\ast h(t)]$

3. 分配律 (Distributive): $f(t)\ast [g(t)+h(t)]=f(t)\ast g(t)+f(t)\ast h(t)$ 这对于分析信号通过并联系统很有用。 在Frequency Domain中即为： $F(\omega )\cdot [G(\omega )+H(\omega )]=F(\omega )\cdot G(\omega )+F(\omega )\cdot H(\omega )$

4. 时移特性 (Time Shift): 如果 $y(t)=f(t)\ast h(t)$，那么 $f(t-t_0)\ast h(t-t_1)=y(t-t_0-t_1)$。 特别地，$f(t-t_0)\ast h(t)=y(t-t_0)$。这表明卷积运算是 时不变 (time invariant) 的。 在Frequency Domain中即为： $Y(\omega )=F(\omega )\cdot H(\omega )\to F(\omega )e^{-j\omega t_0}\cdot H(\omega )=Y(\omega )e^{-j\omega t_0}$

5. 起始点、结束点和宽度 (Start point, End point, Width): 如果 $f(t)$ 在 $t<t_{s,f}$ 时为 0，在 $t>t_{e,f}$ 时为 0 (宽度 $W_f=t_{e,f}-t_{s,f}$)，并且 $h(t)$ 在 $t<t_{s,h}$ 时为 0，在 $t>t_{e,h}$ 时为 0 (宽度 $W_h=t_{e,h}-t_{s,h}$)，那么它们的卷积 $y(t)=f(t)\ast h(t)$：

   • 在 $t<t_{s,y}=t_{s,f}+t_{s,h}$ 时为 0。
   • 在 $t>t_{e,y}=t_{e,f}+t_{e,h}$ 时为 0。
   • 宽度为 $W_y=W_f+W_h$。 这对于检查卷积结果的范围很有帮助。

常见结果 $$rect\left(\frac{t}{T}\right)\ast rect\left(\frac{t}{T}\right)=T\mathrm{\Delta }\left(\frac{t}{2T}\right)$$

冲激 $\delta (t)$ (Impulse) 及其性质

冲激的概念

我们在数学运算中知道，有加法单位元 0 ($f+0=f$) 和乘法单位元 1 ($f\times 1=f$)。那么卷积运算有没有类似的 单位元 (identity element) 呢？也就是说，是否存在一个信号 $p(t)$ 使得对于任意 $f(t)$ 都有 $f(t)\ast p(t)=f(t)$？

答案是肯定的，这个信号就是 狄拉克冲激函数 (Dirac delta function) $\delta (t)$。

严格来说，$\delta (t)$ 不是一个传统意义上的函数，而是一个 分布 (distribution)。我们通常通过它与普通函数的积分或卷积来定义它的行为。

一个理解 $\delta (t)$ 的方式是将其视为一个极限过程：考虑一个宽度为 $ϵ$、高度为 $1/ϵ$ 的矩形脉冲 $p_{ϵ}(t)=\frac{1}{ϵ}\text{rect}(\frac{t}{ϵ})$。这个脉冲的面积始终为 1。当 $ϵ\to 0$ 时，这个脉冲变得无限窄、无限高，但在 $t=0$ 处“集中”了全部的单位面积。

$$\delta (t)=\underset{ϵ\to 0}{lim}{p}_{ϵ}(t)$$

虽然 $\delta (t)$ 在 $t=0$ 时是无限的，并且能量也是无限的，但它的面积是有限的 (等于 1)。

冲激的性质

冲激函数具有许多极其重要的性质：

1. 卷积特性 (Convolution Property) / 单位元 (Identity Element): $f(t)\ast \delta (t)=f(t)$ $f(t)\ast \delta (t-t_0)=f(t-t_0)$ 这正是我们寻找的卷积单位元。与冲激卷积相当于保持原信号不变，与移位冲激卷积相当于将原信号移位。

2. 筛选特性 (Sifting Property): $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(t)\delta (t-t_0)dt=f(t_0)$$ 这是 $\delta (t)$ 最核心和最有用的性质。它表明，冲激函数 $\delta (t-t_0)$ 在积分中起到了“筛选”出函数 $f(t)$ 在 $t=t_0$ 这一点值的效果。 技术比喻: 就像一个筛子，$\delta (t-t_0)$ 只允许 $f(t)$ 在 $t=t_0$ 这一点的值通过积分运算。

3. 采样特性 (Sampling Property): $f(t)\delta (t-t_0)=f(t_0)\delta (t-t_0)$ 这表明一个函数乘以一个冲激，等于该函数在该冲激位置的值乘以该冲激。

4. 面积 (Area): $${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t)dt=1$$

5. 对称性 (Symmetry): $\delta (t)=\delta (-t)$ 冲激函数是偶函数。

6. 尺度变换 (Scaling): $\delta (at)=\frac{1}{|a|}\delta (t)$

7. 积分 (Definite Integral): ${\int }_{-\mathrm{\infty }}^t\delta (\tau )d\tau =u(t)$ (单位阶跃函数 Unit-step function)

8. 单位阶跃函数的导数 (Unit-step Derivative): $\frac{d}{dt}u(t)=\delta (t)$

9. 傅里叶变换 (Fourier Transform): $\mathcal{F}\delta (t)=1$ $\mathcal{F}1=2\pi \delta (\omega )$ 这两个变换对非常重要，尤其是后者，它使得我们可以处理直流 (DC) 和其他功率信号的傅里叶变换。

10. Doublet ${\delta }^{\prime }(t)=\frac{d}{dt}\delta (t)\to f(t)\ast {\delta }^{\prime }(t)=f^{\prime }(t)$

$$Y(\omega )=\frac{\pi }{2+j\omega }\delta (\omega -1)$$

冲激响应 $h(t)$ (Impulse Response)

对于一个 LTI 系统，当输入信号为单位冲激 $\delta (t)$ 时，系统的输出被称为该系统的 冲激响应 (Impulse Response)，记为 $h(t)$。

$$h(t)=\text{System}\delta (t)$$

冲激响应 $h(t)$ 完全刻画了 LTI 系统在 时域 的特性。为什么？因为任何输入信号 $f(t)$ 都可以看作是由无穷多个移位的、加权的冲激组成的 (利用筛选特性反向思考)。由于系统是线性和时不变的，我们可以通过叠加系统对每一个冲激分量的响应来得到总输出。这个叠加过程，正是 卷积！

$$y(t)=f(t)\ast h(t)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(\tau )h(t-\tau )d\tau$$

所以，知道了系统的冲激响应 $h(t)$，我们就可以通过卷积计算出系统对 任意 输入 $f(t)$ 的响应 $y(t)$。$h(t)$ 在时域分析中的地位，就如同频率响应 $H(\omega )$ 在频域分析中的地位。

Example

• 根据Frequency Response计算 $h(t)$

• 根据output计算 $h(t)$

功率信号的傅里叶变换 (Fourier Transform of Power Signals)

我们之前主要处理绝对可积的信号 (能量信号)，它们的傅里叶变换存在。但是像 $\cos ({\omega }_{c}t)$ 或 $u(t)$ 这样的信号，它们的能量是无限的，但功率是有限的，称为 功率信号 (power signals)。

借助冲激函数，我们也可以定义这些功率信号的傅里叶变换

示例讲解

1. $\cos ({\omega }_{c}t)$ 的傅里叶变换

这是功率信号的一个典型例子。我们想求 $F(\omega )=\mathcal{F}\cos ({\omega }_{c}t)$。

1. 利用欧拉公式 (Euler’s Formula): 我们将 $\cos ({\omega }_{c}t)$ 表示为复指数形式： $$\cos ({\omega }_{c}t)=\frac{e^{j{\omega }_{c}t}+e^{-j{\omega }_{c}t}}{2}$$

2. 利用已知的变换对和线性性质: 我们知道复指数信号的傅里叶变换对是： $$e^{j{\omega }_{0}t}\leftrightarrow 2\pi \delta (\omega -{\omega }_0)$$ 这是一个非常关键的变换对，它告诉我们一个单一频率的复指数信号在频域对应一个位于该频率的冲激。 根据傅里叶变换的线性性质，我们可以对上式两项分别进行变换： $$\text{Missing or unrecognized delimiter for left}$$ $$=\frac{1}{2}\mathcal{F}{e}^{j{\omega }_{c}t}+\frac{1}{2}\mathcal{F}{e}^{-j{\omega }_{c}t}$$ $$=\frac{1}{2}[2\pi \delta (\omega -{\omega }_c)]+\frac{1}{2}[2\pi \delta (\omega -(-{\omega }_c))]$$ $$=\pi \delta (\omega -{\omega }_c)+\pi \delta (\omega +{\omega }_c)$$

3. 结果解读: $\cos ({\omega }_{c}t)$ 的傅里叶变换是在频率轴上的 $\omega ={\omega }_c$ 和 $\omega =-{\omega }_c$ 处各有一个强度 (面积) 为 $\pi$ 的冲激。这非常直观地说明了余弦信号的频率成分完全集中在 $\pm {\omega }_c$ 这两个频率点上。 类似地，可以推导出 $\sin ({\omega }_{c}t)\leftrightarrow j\pi [\delta (\omega +{\omega }_c)-\delta (\omega -{\omega }_c)]$ 。

2. 调制信号 $f(t)\cos ({\omega }_{c}t)$ 的傅里叶变换

这个例子展示了 调制 (Modulation) 的过程。假设 $f(t)$ 是一个能量信号 (比如语音或数据信号)，其傅里叶变换为 $F(\omega )$。我们想求 $f(t)\cos ({\omega }_{c}t)$ 的傅里叶变换。

1. 利用调制特性 (Modulation Property): 我们知道傅里叶变换的调制特性： $$f(t)\cos ({\omega }_{c}t)=f(t)\frac{e^{j{\omega }_{c}t}+e^{-j{\omega }_{c}t}}{2}=\frac{1}{2}f(t)e^{j{\omega }_{c}t}+\frac{1}{2}f(t)e^{-j{\omega }_{c}t}$$ 利用频移特性 $\mathcal{F}f(t)e^{j{\omega }_{0}t}=F(\omega -{\omega }_0)$，得到： $$\mathcal{F}f(t)\cos ({\omega }_{c}t)=\frac{1}{2}F(\omega -{\omega }_c)+\frac{1}{2}F(\omega +{\omega }_c)$$

2. 结果解读: 这个结果表明，将信号 $f(t)$ 乘以 $\cos ({\omega }_{c}t)$ (载波 Carrier)，在频域中相当于将原始信号的频谱 $F(\omega )$ 复制两份，分别移动到中心频率 ${\omega }_c$ 和 $-{\omega }_c$ 处，并且幅度减半。这就是幅度调制 (AM) 的基本原理，将低频的基带信号 $f(t)$ 搬移到高频 ${\omega }_c$ 处进行传输。

3.周期信号 (Periodic Signals) 的傅里叶变换

任何一个周期为 $T_0$ 的周期信号 $f(t)$ 都可以用傅里叶级数 (Fourier Series) 表示： $$f(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{c}_n{e}^{jn{\omega }_{0}t}(\text{其中 }{\omega }_0=2\pi /T_0)$$ 其中 $c_n$ 是傅里叶级数系数。 对其求傅里叶变换，利用线性和 $e^{jn{\omega }_{0}t}\leftrightarrow 2\pi \delta (\omega -n{\omega }_0)$： $$\text{Missing or unrecognized delimiter for left}$$ $$F(\omega )=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{c}_n[2\pi \delta (\omega -n{\omega }_0)]=2\pi \sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{c}_n\delta (\omega -n{\omega }_0)$$

结果解读: 周期信号的傅里叶变换是一串位于谐波频率 $n{\omega }_0$ 处的 冲激 (impulses)，每个冲激的强度 (面积) 由对应的傅里叶级数系数 $c_n$ (乘以 $2\pi$) 决定。

4. 冲激串 (Impulse Train) 的傅里叶变换

冲激串本身就是一个周期信号，周期为 $T$： $$p(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-nT)$$ 它的基波频率是 ${\omega }_s=2\pi /T$。我们可以把它看作周期信号的特例来求傅里叶变换。 首先计算它的傅里叶级数系数 $c_n$： $$c_n=\frac{1}{T}{\int }_{-T/2}^{T/2}p(t)e^{-jn{\omega }_{s}t}dt=\frac{1}{T}{\int }_{-T/2}^{T/2}\delta (t)e^{-jn{\omega }_{s}t}dt$$ 根据冲激的筛选特性，积分结果为： $$c_n=\frac{1}{T}{e}^{-jn{\omega }_s(0)}=\frac{1}{T}$$ 所有傅里叶系数都相等，等于 $1/T$。 现在代入周期信号傅里叶变换的公式： $$\mathcal{P}(\omega )=\mathcal{F}p(t)=2\pi \sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{c}_n\delta (\omega -n{\omega }_s)=2\pi \sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{T}\delta (\omega -n{\omega }_s)$$ $$\mathcal{P}(\omega )=\frac{2\pi }{T}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (\omega -n{\omega }_s)={\omega }_s\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (\omega -n{\omega }_s)$$

结果解读: 时域中的冲激串 (间隔 $T$) 对应频域中的冲激串 (间隔 ${\omega }_s=2\pi /T$)。这个变换对在采样理论中至关重要。注意时间和频率间隔的倒数关系。

采样 (Sampling)

采样是连接模拟信号和数字世界的桥梁，是 模数转换 (Analog-to-Digital Conversion) 的第一步。

理想采样过程

理想采样可以看作是将连续时间的模拟信号 $f(t)$ 与一个 冲激串 (impulse train) $p(t)$ 相乘。冲激串是周期为 $T$ 的一系列单位冲激：

$$p(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-nT)$$

其中 $T$ 是 采样周期 (Sampling Period)，$f_s=1/T$ 是 采样频率 (Sampling Frequency) (${\omega }_s=2\pi f_s=2\pi /T$ 是角频率)。

采样后的信号 $f_s(t)$ 为：

$$f_s(t)=f(t)p(t)=f(t)\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-nT)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}f(nT)\delta (t-nT)$$

这表示 $f_s(t)$ 只在 $t=nT$ (采样时刻) 具有非零值 (冲激)，其强度 (面积) 等于原始信号在这些时刻的值 $f(nT)$。

采样在频域的影响

采样在时域是乘以冲激串，在频域则对应于卷积。冲激串的傅里叶变换也是一个冲激串 (频率间隔为 ${\omega }_s$)：

$$\mathcal{F}p(t)=\mathcal{P}(\omega )=\frac{2\pi }{T}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (\omega -n{\omega }_s)={\omega }_s\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (\omega -n{\omega }_s)$$ 傅里叶变换性质: 时域中乘积->频域中卷积除以 $2\pi$

那么采样后信号 $f_s(t)$ 的傅里叶变换 $F_s(\omega )$ 就是原始信号频谱 $F(\omega )$ 与 $\mathcal{P}(\omega )$ 的卷积 (除以 $2\pi$)：

$$F_s(\omega )=\frac{1}{2\pi }F(\omega )\ast \mathcal{P}(\omega )=\frac{1}{T}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}F(\omega -n{\omega }_s)$$

这表明，采样后信号的频谱 $F_s(\omega )$ 是原始信号频谱 $F(\omega )$ 以采样频率 ${\omega }_s$ 为周期进行 周期性延拓 (periodic extension) 的结果，并且幅度被 $1/T$ 缩放。

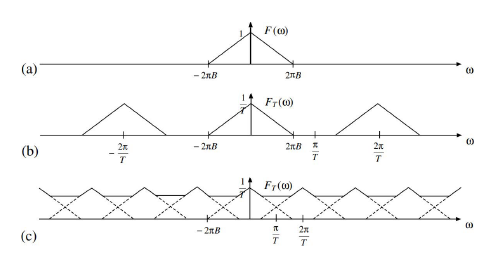
图例分析

• (a) 原始信号频谱 $F(\omega )$: 假设这是一个 带限 (bandlimited) 信号，其最高频率为 ${\omega }_M$ (图中表示为 $2\pi B$)。即 $F(\omega )=0$ 当 $

  \omega

  \omega_M$。

• (b) 采样后频谱 $F_s(\omega )$ (无混叠): 这里展示的是满足 奈奎斯特采样定理 (Nyquist Sampling Theorem) 的情况，即采样频率 ${\omega }_s$ 大于两倍的最高信号频率 (${\omega }_s>2{\omega }_M$)。 $${\omega }_s=\frac{2\pi }{T}>2{\omega }_M(\text{或 }{f}_s>2f_M)$$ 你可以看到，原始频谱 $F(\omega )$ (幅度变为 $1/T$) 被复制并平移到中心频率 $0,\pm {\omega }_s,\pm 2{\omega }_s,\dots$ 处。由于 ${\omega }_s>2{\omega }_M$，这些复制出来的频谱之间没有重叠 (No overlap)。 在这种情况下，我们可以用一个理想低通滤波器 (图中未画出，但截止频率 ${\omega }_c$ 需满足 ${\omega }_M<{\omega }_c<{\omega }_s-{\omega }_M$) 完整地提取出中心部分的频谱 (对应 $n=0$ 的项，即 $\frac{1}{T}F(\omega )$)，从而恢复原始信号 $f(t)$ (除了一个 $1/T$ 的比例因子)。这就是 重建 (Reconstruction) 的基础。

• (c) 采样后频谱 $F_s(\omega )$ (有混叠): 这里展示的是不满足奈奎斯特条件的情况，即采样频率过低 (${\omega }_s<2{\omega }_M$)。 $${\omega }_s=\frac{2\pi }{T}<2{\omega }_M$$ 你可以看到，复制出来的频谱发生了 重叠 (Overlap)。高频部分 ($\omega$ 接近 ${\omega }_M$) 的信息与相邻频谱的低频部分混杂在了一起。这种现象称为 混叠 (Aliasing)。

总结: 采样过程在频域会导致原始频谱的周期性延拓。为了能够从采样后的信号中无失真地恢复原始信号，必须保证采样频率足够高 (${\omega }_s>2{\omega }_M$)，以避免频谱混叠。

重建过程 (The Reconstruction Process)

重建的目标是从采样得到的离散样本序列 $f(nT)$ (或者说，从采样后的冲激串信号 $f_s(t)=\sum f(nT)\delta (t-nT)$) 恢复出原始的连续时间模拟信号 $f(t)$。

这个过程可以从 频域 (Frequency Domain) 和 时域 (Time Domain) 两个角度来理解：

频域角度：理想低通滤波 (Ideal Low-Pass Filtering)

1. 前提条件:

   • 原始信号 $f(t)$ 是 带限 (bandlimited) 的，其频谱 $F(\omega )$ 在最高频率 ${\omega }_M$ 之外为零 ($F(\omega )=0$ for $

     \omega

     \omega_M$)。

   • 采样频率 ${\omega }_s$ 满足 奈奎斯特条件 (Nyquist Criterion): ${\omega }_s>2{\omega }_M$。

2. 采样后的频谱: 我们已经知道，采样后的信号 $f_s(t)$ 的频谱 $F_s(\omega )$ 是原始频谱 $F(\omega )$ 以 ${\omega }_s$ 为周期的无限复制和叠加，并且幅度乘以 $1/T$ : $$F_s(\omega )=\frac{1}{T}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}F(\omega -n{\omega }_s)$$ 因为满足奈奎斯特条件，这些复制的频谱之间没有混叠 (No overlap)。

3. 恢复目标: 我们想要从 $F_s(\omega )$ 中提取出中心的那一份频谱，也就是对应 $n=0$ 的项 $\frac{1}{T}F(\omega )$。如果能得到它，再乘以 $T$，就恢复了原始频谱 $F(\omega )$。

4. 使用理想低通滤波器 (Ideal Low-Pass Filter, LPF): 实现这个提取操作的理想工具就是 理想低通滤波器。我们需要一个滤波器 $H_{LP}(\omega )$，它能：

   • 保留 中心频谱 (即 $

     \omega

     < \omega_M$ 的部分)。

   • 完全滤除 所有其他的频谱副本 (即以 $\pm {\omega }_s,\pm 2{\omega }_s,\dots$ 为中心的部分)。
   • 为了直接得到 $F(\omega )$，我们可以让滤波器的通带增益恰好为 $T$，以抵消 $F_s(\omega )$ 中的 $1/T$ 因子。

5. 滤波器设计: 滤波器的截止频率 ${\omega }_c$ 需要设置在 ${\omega }_M$ 和第一个频谱副本的起始频率 ${\omega }_s-{\omega }_M$ 之间。即： $${\omega }_M<{\omega }_c<{\omega }_s-{\omega }_M$$ (这再次强调了 ${\omega }_s>2{\omega }_M$ 的必要性)。 最常用的选择是将截止频率设在 奈奎斯特频率 (Nyquist Frequency) ${\omega }_s/2$ 处，即 ${\omega }_c={\omega }_s/2=\pi /T$。 因此，理想低通滤波器的频率响应为： $$H_{LP}(\omega )=\{\begin{array}{lll}T& |\omega |<{\omega }_s/20& |\omega |\ge {\omega }_s/2\end{array}$$ 这个形状是一个矩形函数 (Rectangular function)： $$H_{LP}(\omega )=T\cdot \text{rect}\left(\frac{\omega }{{\omega }_s}\right)=T\cdot \text{rect}\left(\frac{\omega T}{2\pi }\right)$$

6. 滤波操作: 将采样后的信号频谱 $F_s(\omega )$ 通过这个滤波器： $$F_{rec}(\omega )=F_s(\omega )\cdot H_{LP}(\omega )=(\frac{1}{T}\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}F(\omega -n{\omega }_s))\cdot (T\cdot \text{rect}\left(\frac{\omega }{{\omega }_s}\right))$$ 由于 $\text{rect}(\omega /{\omega }_s)$ 只在 $|\omega |<{\omega }_s/2$ 区间内为 1，且该区间内只有 $n=0$ 的频谱副本 $F(\omega )$ 存在 (因为 $F(\omega )$ 带限到 ${\omega }_M<{\omega }_s/2$)，所以滤波器的作用是精确地选出 $n=0$ 的项并乘以 $T$，同时将所有 $n\ne 0$ 的项置零。 $$F_{rec}(\omega )=(\frac{1}{T}F(\omega ))\cdot (T)=F(\omega )\text{for }|\omega |<{\omega }_s/2$$ 对于 $|\omega |\ge {\omega }_s/2$，$H_{LP}(\omega )=0$，所以 $F_{rec}(\omega )=0$。 因为原始信号 $f(t)$ 本身就带限在 ${\omega }_M<{\omega }_s/2$ 内，所以我们最终得到的 $F_{rec}(\omega )$ 就等于原始信号的频谱 $F(\omega )$。

时域角度：卷积 (Convolution)

1. 频域相乘 = 时域卷积: 我们知道，在频域中将信号频谱 $F_s(\omega )$ 与滤波器响应 $H_{LP}(\omega )$ 相乘，对应于在时域中将信号 $f_s(t)$ 与滤波器的 冲激响应 (Impulse Response) $h_{LP}(t)$ 进行 卷积。 $$f_{rec}(t)={\mathcal{F}}^{-1}{F}_{rec}(\omega )={\mathcal{F}}^{-1}{F}_s(\omega )H_{LP}(\omega )=f_s(t)\ast h_{LP}(t)$$

2. 滤波器的冲激响应 $h_{LP}(t)$: 我们需要找到理想低通滤波器 $H_{LP}(\omega )=T\cdot \text{rect}(\omega /{\omega }_s)$ 的逆傅里叶变换 (Inverse Fourier Transform)。 回忆傅里叶变换对： $$\frac{W}{2\pi }\text{sinc}\left(\frac{Wt}{2\pi }\right)\leftrightarrow \text{rect}\left(\frac{\omega }{W}\right)$$ (这里我们使用归一化的 sinc 函数定义: $\text{sinc}(x)=\frac{\sin (\pi x)}{\pi x}$) 令 $W={\omega }_s=2\pi /T$，代入上式： $$\frac{2\pi /T}{2\pi }\text{sinc}\left(\frac{(2\pi /T)t}{2\pi }\right)\leftrightarrow \text{rect}\left(\frac{\omega }{2\pi /T}\right)$$ $$\frac{1}{T}\text{sinc}\left(\frac{t}{T}\right)\leftrightarrow \text{rect}\left(\frac{\omega T}{2\pi }\right)=\text{rect}\left(\frac{\omega }{{\omega }_s}\right)$$ 所以，理想低通滤波器的冲激响应为： $$\text{Missing or unrecognized delimiter for left}$$ 因此，理想重建滤波器的冲激响应就是 sinc 函数！

3. 时域重建过程: 将采样信号 $f_s(t)$ 与 sinc 函数 $h_{LP}(t)$ 进行卷积： $$f_{rec}(t)=f_s(t)\ast h_{LP}(t)=(\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}f(nT)\delta (t-nT))\ast \text{sinc}\left(\frac{t}{T}\right)$$ 这个卷积运算就是时域中的重建过程。

重建公式 (The Reconstruction Formula)

现在我们来推导具体的重建公式。利用卷积的线性性质，以及 $\delta (t-t_0)\ast g(t)=g(t-t_0)$ 的性质： $$f_{rec}(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}f(nT)(\delta (t-nT)\ast \text{sinc}\left(\frac{\pi t}{T}\right))$$ $$f_{rec}(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}f(nT)\text{sinc}\left(\frac{\pi (t-nT)}{T}\right)$$

这就是著名的 惠特克-香农插值公式 (Whittaker-Shannon Interpolation Formula)，也称为 基数样条 (Cardinal Spline) 或 sinc(注意此处未归一化)插值。

• 这个公式表明，原始的连续时间信号 $f(t)$ (记为 $f_{rec}(t)$ 以表示它是重建的结果) 可以表示为无穷多个加权的、移位的 sinc 函数的总和。
• 每一项 $f(nT)\text{sinc}\left(\frac{t-nT}{T}\right)$ 代表了在采样时刻 $t=nT$ 获得的样本值 $f(nT)$ 对整个连续信号的贡献。
• $\text{sinc}\left(\frac{t-nT}{T}\right)$ 是一个以 $t=nT$ 为中心，形状为 sinc 的 基函数 (Basis Function) 或 插值函数 (Interpolation Function)。
• 样本值 $f(nT)$ 决定了对应 sinc 基函数的 幅度 (Amplitude) 或 权重 (Weight)。