Fourier Series and LTI System Response to Periodic Signals

#ECE210

周期信号 (Periodic Signals)

定义与基本概念

• 周期性 (Periodicity): 一个信号 $f(t)$ 如果存在一个 非零 时间常数 $t_0$，使得对 所有 时间 $t$ 都满足 $f(t)=f(t-t_0)$，那么这个信号就是周期的。这意味着信号会无限地重复自身的模式。
• 周期 (Period): 满足 $f(t)=f(t-t_0)$ 的 $t_0$ 值有无穷多个 (例如 $2t_0,3t_0,\dots$)。其中，最小的 正值 $t_0$ 被称为 基本周期 (Fundamental Period)，记作 $T$。单位通常是秒 (s)。
• 基本频率 (Fundamental Frequency): 与基本周期 $T$ 对应的是基本角频率 ${\omega }_0$，定义为 ${\omega }_0=\frac{2\pi }{T}$，单位是弧度每秒 (rad/s)。还有一个基本频率 $f_0=1/T$，单位是赫兹 (Hz)。$T$ 和 ${\omega }_0$ (或 $f_0$) 互为反比关系：周期越长，频率越低。

例子:

• $\cos (t)$ 的基本周期 $T=2\pi$ s，基本频率 ${\omega }_0=1$ rad/s。
• $\cos (2t)$ 的基本周期 $T=\pi$ s，基本频率 ${\omega }_0=2$ rad/s。

周期信号的和

• 关键条件: 多个周期信号 $f_1(t),f_2(t),\dots ,f_N(t)$ (各自基本频率为 ${\omega }_1,{\omega }_2,\dots ,{\omega }_N$) 的和 $f(t)=\sum _{i=1}^N{f}_i(t)$ 是否为周期信号，取决于这些频率之间的关系。当且仅当所有不同频率两两之间的比率 ${\omega }_i/{\omega }_j$ 均为有理数时，和信号 $f(t)$ 才是周期的。
  • 有理数: 可以表示为两个整数之比的数 (如 1/2, 3, 2/3)。
  • 无理数: 不能表示为两个整数之比的数 (如 $\pi ,\sqrt{2},\pi /2$)。
• 和信号的周期与频率:
  • 如果和信号是周期的，其基本频率 ${\omega }_0$ 是所有单个信号频率 ${\omega }_i$ 的 最大公约数 (Greatest Common Divisor, GCD): $${\omega }_0=\text{GCD}({\omega }_1,{\omega }_2,\dots ,{\omega }_N)$$ 这个 ${\omega }_0$ 是最大的能被所有 ${\omega }_i$ 整除的频率 (或者说，所有 ${\omega }_i$ 都是 ${\omega }_0$ 的整数倍)。
  • 相应地，和信号的基本周期 $T$ 是所有单个信号周期 $T_i=2\pi /{\omega }_i$ 的 最小公倍数 (Least Common Multiple, LCM): $$T=\text{LCM}(T_1,T_2,\dots ,T_N)$$ 这个 $T$ 是所有信号同时完成整数个周期并回到初始相对状态所需的最小时间。
  • $T$ 和 ${\omega }_0$ 仍然满足 $T=2\pi /{\omega }_0$。

例子 (来自 Slides):

• $f(t)=\cos (t)+\cos (2t)$: ${\omega }_1=1,{\omega }_2=2$。比率 $1/2$ 是有理数。${\omega }_0=\text{GCD}(1,2)=1$ rad/s, $T=\text{LCM}(2\pi ,\pi )=2\pi$ s。信号是周期的。
• $g(t)=\cos (t)+\cos (\frac{3}{2}t)$: ${\omega }_1=1,{\omega }_2=3/2$。比率 $1/(3/2)=2/3$ 是有理数。${\omega }_0=\text{GCD}(1,3/2)=1/2$ rad/s, $T=\text{LCM}(2\pi ,4\pi /3)=4\pi$ s。信号是周期的。
• $f_1(t)=\cos (\pi t)+\cos (2t)$: ${\omega }_1=\pi ,{\omega }_2=2$。比率 $\pi /2$ 是无理数。信号 不是 周期的。

傅里叶级数 (Fourier Series)

核心思想

傅里叶级数是一种将 周期信号 分解为一系列具有 谐波关系 (harmonically related) 的简单正弦/余弦波或复指数函数之和的方法。这里的谐波关系意味着这些简单波的频率都是 基本频率 ${\omega }_0$ 的整数倍 ($0,{\omega }_0,2{\omega }_0,3{\omega }_0,\dots$)。

• 类比: 就像把复杂的音乐和弦分解成构成它的单个音符 (基音和泛音)，或者把混合光分解成其光谱成分 (不同颜色的光波)。傅里叶级数提供了分析和表示复杂周期现象的基本工具。

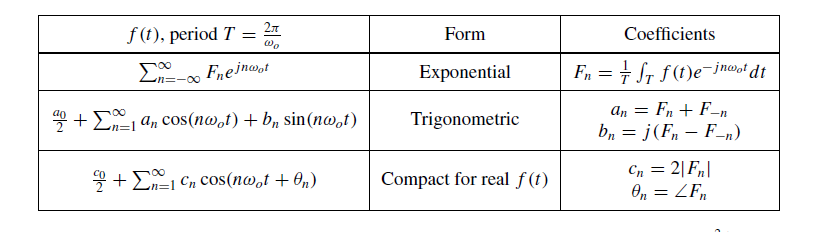
指数形式傅里叶级数 (Exponential Fourier Series)

这是最常用、最紧凑且数学上最方便的形式。任何满足狄利克雷条件的周期信号 $f(t)$ (周期 $T$, 频率 ${\omega }_0$) 都可以表示为： $$f(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{F}_n{e}^{jn{\omega }_{0}t}$$

• 基函数 (Basis Functions): $e^{jn{\omega }_{0}t}$ 是一组无限的复指数函数，频率分别为 $\dots -2{\omega }_0,-{\omega }_0,0,{\omega }_0,2{\omega }_0,\dots$。它们构成了信号空间的一组 正交基。

• 傅里叶系数 (Fourier Coefficients): $F_n$ 是一个 复数，代表了频率为 $n{\omega }_0$ 的分量在 $f(t)$ 中的 权重。$F_n$ 包含了该频率分量的 幅度和相位 信息 ($F_n =

  F_n

  e^{j \angle F_n}$)，\mathrm{并}\mathrm{且}$F_n$ 是 与时间无关 的常数。

  • $F_0$: 对应 $n=0$ (频率为 0)，代表信号的 直流 (DC) 分量 或 平均值。
  • $F_1,F_{-1}$: 对应 $n=\pm 1$，代表 基频 (${\omega }_0$) 分量。
  • $F_n,F_{-n}$: 对应 $n=\pm k$，代表 k 次谐波 ($k{\omega }_0$) 分量。

计算傅里叶系数 $F_n$

系数 $F_n$ 通过以下积分计算得到，这个过程可以理解为将信号 $f(t)$ 投影 (project) 到基函数 $e^{jn{\omega }_{0}t}$ 上： $$F_n=\frac{1}{T}{\int }_{T}f(t)e^{-jn{\omega }_{0}t}dt$$

• 积分区间 ${\int }_T$: 可以在 任何一个完整的周期 上进行积分，常用的区间是 $[0,T]$ 或 $[-T/2,T/2]$。结果与选择哪个周期无关。
• 正交性: 计算公式的来源是基函数的正交性。在一个周期 $T$ 内积分： $$\frac{1}{T}{\int }_T(e^{jn{\omega }_{0}t})(e^{-jm{\omega }_{0}t})dt=\{\begin{array}{ll}1& \text{if }n=m\\ 0& \text{if }n\ne m\end{array}$$ 这意味着不同频率的基函数是相互正交的，像坐标系中的 x, y, z 轴一样。投影操作可以精确地提取出信号中特定频率分量的复幅度 $F_n$。

傅里叶系数的解释

• $F_0=\frac{1}{T}{\int }_{T}f(t)dt$ 是信号 $f(t)$ 在一个周期内的 时间平均值 (time average)。

• $

  F_n

  $\mathrm{是}\mathrm{频}\mathrm{率}\mathrm{为}$n\omega_0$ 的谐波分量的 幅度 (amplitude)。

• $\mathrm{\angle }{F}_n$ 是频率为 $n{\omega }_0$ 的谐波分量的 相位 (phase)。
• 对于实信号 $f(t)$: 系数具有 共轭对称性 (conjugate symmetry) 或 厄米对称性 (Hermitian symmetry): $F_{-n}=F_n^{\ast }$。

  • 这意味着 $

    F_{-n}

    =

    F_n

    $ (幅度谱是偶对称的)。

  • $\mathrm{\angle }{F}_{-n}=-\mathrm{\angle }{F}_n$ (相位谱是奇对称的)。
  • 这个性质使得我们只需要计算 $n\ge 0$ 的系数就可以知道所有系数。

其他形式的傅里叶级数

• 三角形式 (Trigonometric Form): $$f(t)=\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}(a_n\cos (n{\omega }_{0}t)+b_n\sin (n{\omega }_{0}t))$$ 系数关系 (对于实信号): $a_0=2F_0$, $a_n=2\text{Re}{F}_n$, $b_n=-2\text{Im}{F}_n$ for $n\ge 1$.
• 紧凑形式 (Compact Form) (仅对实信号): $$f(t)=\frac{c_0}{2}+\sum _{n=1}^{\mathrm{\infty }}{c}_n\cos (n{\omega }_{0}t+{\theta }_n)$$ 系数关系: $c_0=2F_0=a_0$, $c_n=2|F_n|=\sqrt{a_n^2+b_n^2}$, ${\theta }_n=\mathrm{\angle }{F}_n=\text{atan2}(-b_n,a_n)$ for $n\ge 1$. $c_n$ 直接表示了第 n 次谐波的幅度，${\theta }_n$ 是其相位。

存在条件 (狄利克雷条件 Dirichlet Conditions)

傅里叶级数能够收敛于原信号 $f(t)$ (在连续点处) 的充分条件：

• $f(t)$ 在一个周期内 绝对可积 ($\int_T

  f(t)

  dt < \infty$)。

• $f(t)$ 在一个周期内只有 有限个极大值和极小值。
• $f(t)$ 在一个周期内只有 有限个不连续点 (跳变点)。在不连续点处，傅里叶级数收敛到该点 左右极限的平均值 (中点值)。 工程中遇到的大多数周期信号都满足这些条件。

傅里叶级数的重要性质

• 线性 (Linearity): 如果 $f(t)\leftrightarrow F_n$ 且 $g(t)\leftrightarrow G_n$，则 $af(t)+bg(t)\leftrightarrow a{F}_n+b{G}_n$。
• 时移 (Time Shift): 如果 $f(t)\leftrightarrow F_n$，则 $f(t-t_0)\leftrightarrow F_n{e}^{-jn{\omega }_0{t}_0}$。时移只改变相位，不改变幅度。
• 频率移动 (Frequency Shift): $f(t)e^{jM{\omega }_{0}t}\leftrightarrow F_{n-M}$ (指数形式中不常用，但在其他变换中重要)。
• 时间/频率缩放 (Scaling): 改变周期 $T$ 会同时改变频率 ${\omega }_0$ 和系数 $F_n$。
• 时间微分 (Time Differentiation): 如果 $f(t)\leftrightarrow F_n$，则 $\frac{df(t)}{dt}\leftrightarrow (jn{\omega }_0)F_n$。微分增强高频分量。
• 时间积分 (Time Integration): 如果 $f(t)\leftrightarrow F_n$ 且 $F_0=0$，则 $\int f(t)dt\leftrightarrow \frac{F_n}{jn{\omega }_0}$。积分增强低频分量。
• 共轭对称性 (Conjugate Symmetry): 对实信号 $f(t)$, $F_{-n}=F_n^{\ast }$。
• 帕塞瓦尔定理 (Parseval’s Theorem): 信号在一个周期内的 平均功率 (Average Power) 可以通过时域积分计算，也可以通过频域系数计算： $$P=\frac{1}{T}{\int }_T|f(t){|}^{2}dt=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}|F_n{|}^2$$ 对于实信号，也可以用紧凑形式表示: $$P=(\frac{c_0}{2}{)}^2+\frac{1}{2}\sum _{n=1}^{\mathrm{\infty }}{c}_n^2=F_0^2+2\sum _{n=1}^{\mathrm{\infty }}|F_n{|}^2$$ 这说明信号的总能量 (功率) 在时域和频域表示中是守恒的，只是分布在不同的基上。

LTI 系统对周期输入的响应 (LTI System Response to Periodic Inputs)

基本原理：特征函数

• 复指数信号 $e^{j\omega t}$ 是 线性时不变 (LTI) 系统的 特征函数 (eigenfunction)。
• 当 $e^{j\omega t}$ 输入 LTI 系统时，输出是 相同形式 的信号乘以一个复数常数，这个常数就是系统在该频率 $\omega$ 下的 频率响应 (Frequency Response) $H(\omega )$ (即特征值 eigenvalue): $$e^{j\omega t}\stackrel{\text{LTI System }H(\omega )}{\to }H(\omega )e^{j\omega t}$$
• 对于余弦输入 $A\cos (\omega t+\theta )$，利用欧拉公式和叠加原理，输出为: $$A\cos (\omega t+\theta )\stackrel{\text{LTI System }H(\omega )}{\to }A|H(\omega )|\cos (\omega t+\theta +\mathrm{\angle }H(\omega ))$$ 输出仍然是同频率的余弦波，但 幅度 乘以 $|H(\omega )|$，相位 加上 $\mathrm{\angle }H(\omega )$。

利用傅里叶级数分析响应

• 输入信号: 周期信号 $f(t)$，其傅里叶级数为 $f(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{F}_n{e}^{jn{\omega }_{0}t}$。
• LTI 系统: 频率响应为 $H(\omega )$。
• 分析步骤:
  1. 分解输入: 将输入 $f(t)$ 看作是无穷多个复指数分量 $F_n{e}^{jn{\omega }_{0}t}$ 的叠加。
  2. 计算各分量响应: 对于第 $n$ 个分量 $F_n{e}^{jn{\omega }_{0}t}$，其频率为 $n{\omega }_0$。根据特征函数原理，系统对此分量的响应是 $H(n{\omega }_0)\times (F_n{e}^{jn{\omega }_{0}t})$。
  3. 叠加响应: 由于系统是线性的，总输出 $y(t)$ 是所有单个分量响应的叠加： $$y(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}H(n{\omega }_0)F_n{e}^{jn{\omega }_{0}t}$$

输出信号的特性

• 周期性: 输出信号 $y(t)$ 也是一个 周期信号。
• 频率: 输出信号 $y(t)$ 的 基本频率仍然是 ${\omega }_0$，与输入信号相同 (除非 $H(n{\omega }_0)$ 特别地使 $H(\pm {\omega }_0)=0$)。
• 输出傅里叶系数: 输出信号 $y(t)$ 的傅里叶级数系数 $Y_n$ 为： $$Y_n=H(n{\omega }_0)F_n$$
• 系统作用: LTI 系统对其周期输入的响应，可以理解为系统对其输入的 每一个谐波分量 进行了 独立的 幅度和相位调整。调整的比例和相移由系统在 该谐波频率 ($n{\omega }_0$) 处的频率响应 $H(n{\omega }_0)$ 决定。

  • $

    Y_n

    =

    H(n\omega_0)

    F_n

    $ (输出幅度 = 系统增益 × 输入幅度)

  • $\mathrm{\angle }{Y}_n=\mathrm{\angle }H(n{\omega }_0)+\mathrm{\angle }{F}_n$ (输出相位 = 系统相移 + 输入相位)

例子 (来自 Slides):

• 方波通过低通滤波器: (Wang Slide 33-34, 37) 输入方波 $f(t)$ 含有丰富的奇次谐波 ($F_n\propto 1/n$ for odd n)。低通滤波器 $H(\omega )$ 在低频处 $

  H(\omega)

  \approx 1$,\mathrm{在}\mathrm{高}\mathrm{频}\mathrm{处}$

  H(\omega)

  \ll 1$。\mathrm{因}\mathrm{此}，\mathrm{输}\mathrm{出}\mathrm{信}\mathrm{号}$y(t)$\mathrm{的}\mathrm{傅}\mathrm{里}\mathrm{叶}\mathrm{系}\mathrm{数}$Y_n = H(n\omega_0) F_n$\mathrm{中}，\mathrm{低}\mathrm{次}\mathrm{谐}\mathrm{波}(n\mathrm{较}\mathrm{小})\mathrm{的}\mathrm{幅}\mathrm{度}$

  Y_n

  $\mathrm{与}$

  F_n

  $\mathrm{接}\mathrm{近}，\mathrm{而}\mathrm{高}\mathrm{次}\mathrm{谐}\mathrm{波}(n\mathrm{较}\mathrm{大})\mathrm{的}\mathrm{幅}\mathrm{度}$

  Y_n

  $ 被显著 衰减。这导致输出信号 $y(t)$ 比输入方波 $f(t)$ 更平滑，失去了陡峭的边沿 (高频成分)。

Total Harmonic Distortion

好的，我们来详细解释一下 总谐波失真 (Total Harmonic Distortion, THD)。

什么是谐波 (Harmonics)？

• 基波 (Fundamental Frequency): 当我们给一个系统（比如一个放大器或电力系统）输入一个理想的正弦波信号时，这个输入信号的频率称为 基波频率 (fundamental frequency)，通常记为 $f_0$ 或 $f_1$。
• 谐波 (Harmonics): 在一个理想的 线性 (linear) 系统中，输出信号应该只包含与输入信号相同频率（基波频率）的分量，可能振幅和相位有所改变。然而，在 非线性 (non-linear) 系统中，当输入一个频率为 $f_0$ 的正弦波时，输出信号不仅包含基波频率 $f_0$，还会产生新的频率分量，这些新频率是基波频率的整数倍：$2f_0,3f_0,4f_0,\dots$。这些由系统非线性产生的额外频率分量就称为 谐波。
  • $2f_0$: 二次谐波 (2nd harmonic)
  • $3f_0$: 三次谐波 (3rd harmonic)
  • 以此类推…

技术比喻 (Technical Analogy): 想象你用一个完美的音叉敲击，它只发出一个纯粹的音调（基波）。但如果你用这个音叉去敲击一个不完美的物体（非线性系统），除了听到音叉本身的音调外，你可能还会听到一些额外的、更高音调的泛音（谐波），这些泛音是基波频率的整数倍。

什么是总谐波失真 (THD)？

总谐波失真 (Total Harmonic Distortion, THD) 是一个用来量化一个系统（或信号）由于非线性而产生的谐波失真程度的指标。它衡量的是 所有谐波分量的总能量（或幅度） 与 基波分量能量（或幅度） 的比值。

简单来说，THD 告诉你输出信号中有多少成分是由不希望产生的谐波组成的，相对于你真正想要的基波成分。

如何计算 THD？

$P_y$ 可从对 $y(t)$ 积分角度计算

THD 的意义是什么？

THD 是衡量系统 线性度 (linearity) 或信号 保真度 (fidelity) 的重要指标。

• 低 THD (Low THD): 表示系统非线性小，产生的谐波分量很少，输出信号非常接近理想的、未经失真的输入信号（仅考虑谐波失真）。这在 高保真音响 (high-fidelity audio) 系统中非常重要，因为低 THD 意味着声音更纯净、更接近原始录音。在 电力系统 (power systems) 中，低 THD 的电压意味着供电质量好，对用电设备损害小。
• 高 THD (High THD): 表示系统非线性严重，产生了大量的谐波分量，输出信号与输入信号相比有明显的失真。
  • 在 音频 中，高 THD 会导致声音听起来粗糙、刺耳或不自然（尽管有时在电吉他效果器中会故意引入失真作为一种艺术效果）。
  • 在 电力系统 中，由非线性负载（如开关电源、变频器、节能灯）产生的电流谐波会导致电网电压波形畸变 (高电压 THD)，这会引起：
    • 变压器、电缆、电机等设备额外发热，降低效率和寿命。
    • 中性线电流过大（特别是三次谐波）。
    • 保护装置误动作。
    • 对通信系统产生干扰。
    • 精密仪器工作不正常。