Frequency Response of LTI Systems
#ECE210
LTI 系统的频率响应 $H(\omega)$ (The Frequency Response $H(\omega)$ of LTI Systems)
1. 定义: 对于一个 LTI 系统，当输入信号为复指数信号 $f(t) = F e^{j\omega t}$ (其中 $F$ 是复数振幅，代表幅度和初始相位) 时，其稳态输出信号同样是同频率的复指数信号，形式为 $y(t) = Y e^{j\omega t}$。频率响应 $H(\omega)$ 定义为输出相量 (Phasor) $Y$ 与输入相量 $F$ 的比值，它是一个关于角频率 $\omega$ 的复数函数： $$H(\omega) = \frac{Y}{F}$$ 这个定义是基于相量法的。对于实际的余弦输入信号 $f(t) = |F|\cos(\omega t + \angle F) = \text{Re}{F e^{j\omega t}}$, 其对应的稳态输出为 $y(t) = |Y|\cos(\omega t + \angle Y) = \text{Re}{Y e^{j\omega t}}$ 。通过 $Y = H(\omega)F$ 的关系，我们可以得到输出信号的幅度和相位。
2. 计算方法: 1. 电路系统: 将电路转换到相量域 (Phasor Domain)，即： * 电阻 $R$ 的阻抗 (Impedance) 为 $Z_R = R$ * 电感 $L$ 的阻抗为 $Z_L = j\omega L$ * 电容 $C$ 的阻抗为 $Z_C = \frac{1}{j\omega C}$ * 电源 $v(t)$ 或 $i(t)$ 用其相量 $V$ 或 $I$ 表示。 2. 使用电路分析方法 (如节点电压法、网孔电流法、电压/电流 Divider Rule) 计算输出相量 $Y$ (通常是电压或电流相量) 与输入相量 $F$ (通常是源的相量) 的比值，即得到 $H(\omega)$ 。 3. 系统由微分方程描述: $H(\omega)$ 也可以通过系统的常微分方程 (ODE) 得到。
[!tip] Summary
- 可以直接根据电压或者电流的分压分流关系计算得到
3. $H(\omega)$ 的形式: $H(\omega)$ 是一个复数，可以表示为幅度和相位的形式： $$H(\omega) = |H(\omega)| e^{j\angle H(\omega)}$$ 其中 $|H(\omega)|$ 称为 幅度响应 (Magnitude Response)，$\angle H(\omega)$ 称为 相位响应 (Phase Response)。
LTI 电路频率响应 $H(\omega)$ 的性质 (Properties of Frequency Response $H(\omega)$ of LTI Circuits)
- 共轭的性质 核心性质为: $$ H(-\omega) = H^{*}(\omega) $$ $\omega$ 仅通过电容或电感影响 $H(\omega)$ ，当代入 $-\omega$ 时即为 $H(\omega)$ 的共轭
原因： $H(\omega)$ 与 $\omega$ 仅通过电路中的电容与电感建立关系，所以我们只需分析电路中的电容与电感受到 $\omega$ 的影响
- 模场关于输入频率为偶函数
- 辐角关于输入频率为奇函数
- 对于LTI系统中稳态输入的输出结果
常见的稳态输入如,对于LTI系统中的稳态输入直接乘上Frequency Response即可
- $\sin( \omega t)$ 写成phase form为 $F=-j$
- $\cos(\omega t)$ 写成phase form为 $F = 1$
LTI 系统对单频余弦输入的响应 (LTI System Response to Co-Sinusoidal Inputs)
-
这是频率响应最直接的应用。如果 LTI 系统的输入是 $f(t) = F \cos(\omega t + \angle F)$，那么系统的稳态输出 $y(t)$ 是： $$y(t) = F H(\omega) \cos(\omega t + \angle F + \angle H(\omega))$$ -
关键点:
- 输出信号仍然是与输入信号相同频率 $\omega$ 的余弦信号。LTI 系统不会产生新的频率。
-
输出信号的幅度是输入幅度的 $ H(\omega) $ 倍。 - 输出信号的相位是在输入相位的基础上再叠加 $\angle H(\omega)$。
-
示例 (Slides 中的例子):
-
RC 低通滤波器 (Low-pass Filter) $H(\omega) = \frac{1}{1+j\omega RC}$。$ H(\omega) = \frac{1}{\sqrt{1+(\omega RC)^2}}$ 在低频时 ($\omega \approx 0$) 接近 1，在高频时 ($\omega \to \infty$) 趋近于 0。$\angle H(\omega) = -\arctan(\omega RC)$ 从 $0$ 变化到 $-\pi/2$。它允许低频信号通过，衰减高频信号。 -
RC 高通滤波器 (High-pass Filter) : $H(\omega) = \frac{j\omega RC}{1+j\omega RC}$。$ H(\omega) = \frac{\omega RC}{\sqrt{1+(\omega RC)^2}}$ 在低频时趋近于 0，在高频时趋近于 1。它允许高频信号通过，衰减低频信号。 -
RLC 带通滤波器 (Band-pass Filter) $H(\omega) = \frac{j\omega C}{1 - \omega^2 LC + j\omega RC}$。$ H(\omega) $ 在某个中心频率附近较大，而在低频和高频时都趋近于 0。它允许特定频段的信号通过，衰减其他频率的信号。
-
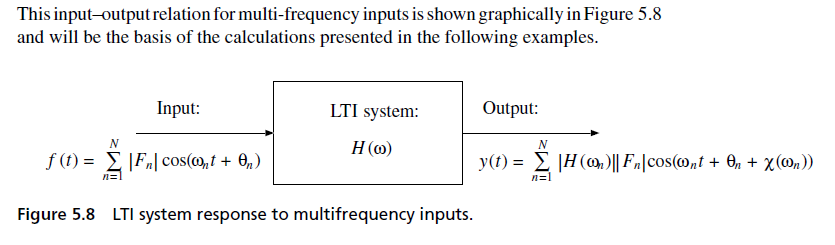
LTI 系统对多频输入的响应 (LTI System Response to Multifrequency Inputs)
- 利用 LTI 系统的叠加原理 (Superposition Principle)。
- 如果输入信号是多个不同频率余弦信号 (以及可能的直流分量) 的和： $$f(t) = F_0 + \sum_{k=1}^{N} |F_k|\cos(\omega_k t + \angle F_k)$$ (其中 $F_0$ 是直流分量，即频率 $\omega=0$ 的分量 )
- 那么系统的稳态输出是每个频率分量单独响应的叠加： $$y(t) = H(0)F_0 + \sum_{k=1}^{N} |F_k||H(\omega_k)|\cos(\omega_k t + \angle F_k + \angle H(\omega_k))$$
-
计算步骤:
- 将输入信号分解为直流分量和各次谐波分量 (或不同频率的正弦/余弦分量)。
- 计算系统在每个频率 ($\omega=0, \omega_1, \omega_2, …$) 处的频率响应值 $H(0), H(\omega_1), H(\omega_2), …$。
-
对每个输入分量，根据 $y_k(t) = F_k H(\omega_k) - 将所有输出分量相加得到最终的总输出 $y(t)$。
-
技术比喻: 这就像一个音响系统的均衡器 (Equalizer)。输入的音乐包含各种频率的声音。均衡器 ($H(\omega)$) 对不同频率（如低音 Bass $\omega_{low}$、中音 Mid $\omega_{mid}$、高音 Treble $\omega_{high}$）有不同的增益 ($ H(\omega) $) 和相位调整 ($\angle H(\omega)$)。输出的声音就是所有频率成分经过各自调整后叠加的结果。
Decibel Amplitude Response
分贝的转化
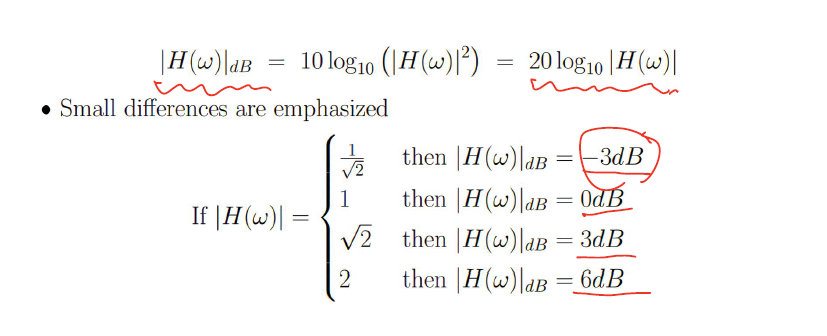
谐振和无损系统 (Resonant and Non-Dissipative Systems)
-
谐振 (Resonance): 指系统在某个特定频率 (谐振频率 $\omega_0$) 附近，其幅度响应 $ H(\omega) $ 出现显著峰值的现象。这意味着系统对该频率的输入信号有特别强的响应。RLC 电路是典型的会发生谐振的电路。 - 无损系统 (Non-Dissipative Systems): 指不包含能量耗散元件 (如电阻 R) 的系统，例如理想的 LC 电路。对这类系统的分析可能需要不同的方法，或者说，使用 $H(\omega)$ 分析稳态响应时需要特别注意（例如，理想 LC 电路在谐振频率驱动下，理论上响应会无限增大，这在物理上不可持续，通常需要考虑初始条件或微小的损耗）。本章主要关注包含耗散元件的系统，其稳态响应是明确的。
[!warning] 注意对于无损系统不能采用上述计算Frequency Response的方法直接计算（因为对于有界的输入可能产生无界的输出）