Motivation

[!Important] 为什么采用 CNN

  • 计算开销

传统的全连接层架构在处理维数非常高的参数数据时所带来的参数开销几乎无法接受，训练效率与成本无法接受

  • 特征捕获能力

全连接层架构将所有的输入都展平，丧失了样本数据原有的空间特征

我们希望有操作能够同时满足以下性质:

  • 平移不变性： 图形的特征并不因平移而改变
  • 局部性：神经网络前几层仅探索局部性质
    我们将 $[H]{ij}$ 记为隐藏层的输出， 其对应的输入为 $[X]{ij}$(图像在位置 (i,j) 所对应的像素)

$$

[H]{ij} = [U]{ij} + \sum_{k}\sum_{j}[W]{i,j,k,l}[X]{k,l} = [U]{ij} + \sum{a}\sum_{b}[V]{i,j,a,b}[X]{i+a,j+b}

$$

交换求和顺序，将权重的索引下标定义为与 (i,j) 相关
我们再满足其局部性,通过限制 a,b 的下标浮动,同时为了支持输入与输出中的多个通道，我们添加第四个坐标

$$ [H]{i,j,d} = u + \sum{a=-\Delta}^{\Delta}\sum {b=-\Delta}^{\Delta}\sum{c}[V]{a,b,c,d}[X]{i+a,j+b,c} $$

其中 H 中的索引 d 表示输出通道，而随后的输出继续进入下一个卷积层

其中 V 即为卷积核，又被称为 kernel 或 filter

卷积核的填充 (Padding) 与步幅 (Stride)

Padding

在我们对图像进行卷积操作时，生成的新图像大小往往会比原来的图像小，如果我们想要保持或者控制生成的新图像的尺寸，我们可以考虑对图像进行填充
同时填充有利于增加边缘像素的权重，防止检测过程中边缘丢失

  • Valid Convolution: 不填充
  • Same Convolution: 填充
    卷积核的长宽通常为奇数，一方面图像具有中心点，便于指出 Filter 位置，另一方面便于填充

Stride

Stride 决定了卷积核在输入数据上每步移动的距离，有时为了搞笑采样或者压缩采样次数，我们可以跳过中间元素
综合步长、填充，我们可以给出卷积最终输出的图像尺寸公式:
对于 $nn$ 的图像与 $ff$ 的卷积核，我们有

$$ size = \left[ \frac{n+2p-f}{s} \right] +1 $$

高维卷积

对于高维图像 (有多个 channel)，我们只需将单层卷积核堆叠升维至与输入图像匹配的 channel,或者叫深度
同时，我们通过定义不同的卷积核生成多维输出通道

1 $\cdot$ 1 卷积

1 $$ 1 卷积本质上即为对多个通道中的输入施加权重产生新的输出并将其叠加，相当于全连接层
1 $$ 1 通道常用于调整网络层的通道数量与控制模型复杂度

Notation

在一层卷积神经网络中：

$$ \begin{align} & \text{input}: n ^{l-1}{h}n ^{l-1}{w} n ^{l-1}{c} , \text{output}: n ^{l-1}{h} n ^{l-1}{w} n ^{l-1}{c}
& f^{l}: filter size, p^{l}: padding, s^{l}: stride
& n ^{l}{c}: \text{number of filters}
& \text{Each filter}: f^{l}\cdot f^{l} \cdot n ^{l-1}{c}
& \text{Activation}: n ^{l}{h}\cdot n ^{l}{w}\cdot n ^{l}_{c} \end{align} $$

卷积神经网络

汇聚层（Pooling Layer)

通常当我们处理图像时，我们希望逐渐降低隐藏表示的空间分辨率、聚集信息，这样随着我们在神经网络中层叠的上升，每个神经元对其敏感的感受野（输入）就越大。
而我们的机器学习任务通常会跟全局图像的问题有关（例如，“图像是否包含一只猫呢？”），所以我们最后一层的神经元应该对整个输入的全局敏感。通过逐渐聚合信息，生成越来越粗糙的映射，最终实现学习全局表示的目标，同时将卷积图层的所有优势保留在中间层。
汇聚层双重目的：降低卷积层对位置的敏感性，同时降低对空间降采样表示的敏感性。

  1. Max Pooling
    提取 Kernel 内的最大元素值
  2. Average Pooling
    将 Kernel 内所有元素值平均

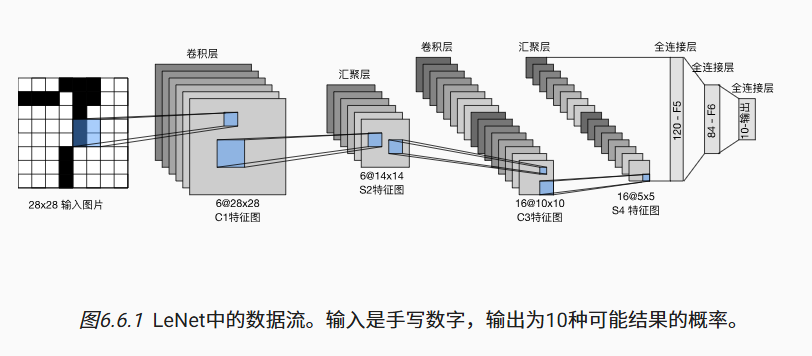
LeNet

259223fe877e4070563a35a0c063e40.png



1
2
3
4
5
6
7
8
9
10
11
12
13



import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

可学习的范式: 一个卷积层后面添加池化层

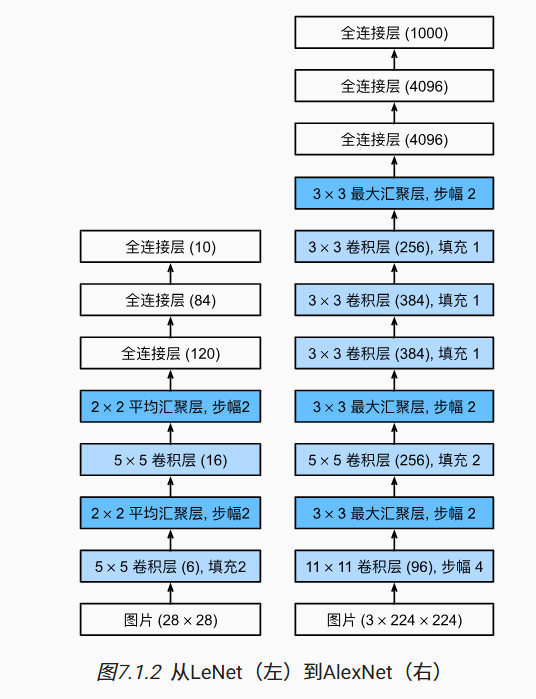
AlexNet

864e99afd3fae103cc1e37e613f8642.png



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28



import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    # 这里使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

设计思路

VGG 网络

经典卷积神经网络的基本组成部分是下面的这个序列：

  1. 带填充以保持分辨率的卷积层；
  2. 非线性激活函数，如 ReLU；
  3. 汇聚层，如最大汇聚层。

而一个 VGG 块与之类似，由一系列卷积层组成，后面再加上用于空间下采样的最大汇聚层。在最初的 VGG 论文中 (Simonyan and Zisserman, 2014)，作者使用了带有 3×3 卷积核、填充为 1（保持高度和宽度）的卷积层，和带有 2×2 汇聚窗口、步幅为 2（每个块后的分辨率减半）的最大汇聚层。
VGG 块



1
2
3
4
5
6
7
8
9
10
11
12
13



import torch
from torch import nn
from d2l import torch as d2l

def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

VGG 网络
VGG 网络将多个 VGG 块相连接，我们可以通过 conv_arch 指定每个 VGG 块中的卷积层数与输出通道数



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16



def vgg(conv_arch):
    conv_blks = []
    in_channels = 1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))

net = vgg(conv_arch)

NiN(网络中的网络)

LeNet、AlexNet 和 VGG 都有一个共同的设计模式：通过一系列的卷积层与汇聚层来提取空间结构特征；然后通过全连接层对特征的表征进行处理。 AlexNet 和 VGG 对 LeNet 的改进主要在于如何扩大和加深这两个模块。 或者，可以想象在这个过程的早期使用全连接层。然而，如果使用了全连接层，可能会完全放弃表征的空间结构。 NiN 提供了一个非常简单的解决方案：在每个像素的通道上分别使用多层感知机 (Lin et al., 2013)
NiN 块
卷积层的输入和输出由四维张量组成，张量的每个轴分别对应样本、通道、高度和宽度。 另外，全连接层的输入和输出通常是分别对应于样本和特征的二维张量。NiN 的想法是在每个像素位置（针对每个高度和宽度）应用一个全连接层。 如果我们将权重连接到每个空间位置，我们可以将其视为 1×1 卷积层，或作为在每个像素位置上独立作用的全连接层。 从另一个角度看，即将空间维度中的每个像素视为单个样本，将通道维度视为不同特征（feature）。
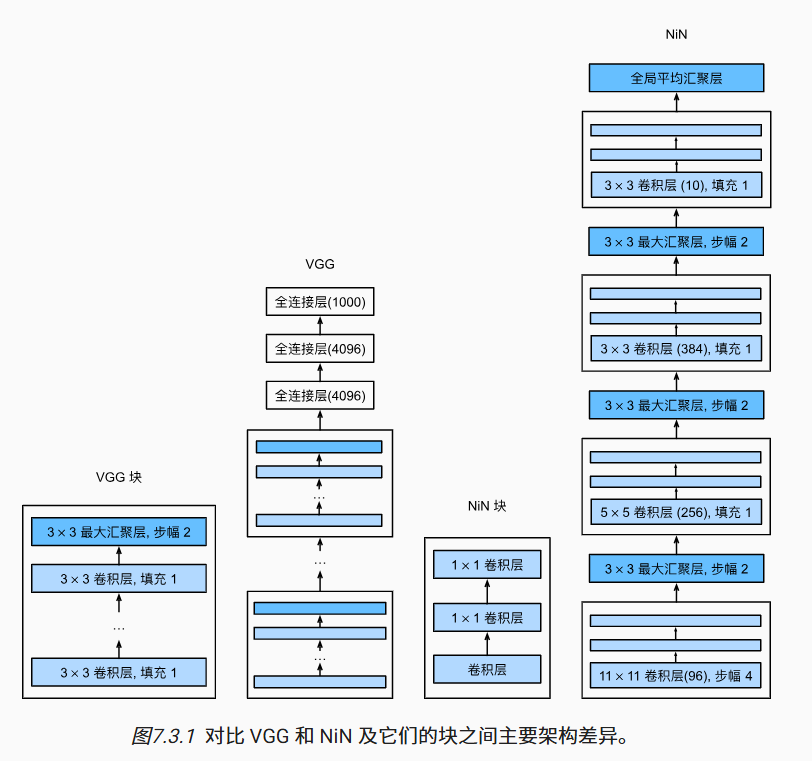
40834b522fcd7fe99f13c3defc58f61.png
一个经典的 NiN 块包括一个传统的卷积层（后面接非线性层），再加上两个 $1*1$ 的卷积层对整个样本中像素点进行采样



1
2
3
4
5
6
7
8
9
10



import torch
from torch import nn
from d2l import torch as d2l

def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

NiN 网络
NiN 和 AlexNet 之间的一个显著区别是 NiN 完全取消了全连接层。 相反，NiN 使用一个 NiN 块，其输出通道数等于标签类别的数量。最后放一个 _ 全局平均汇聚层 _（global average pooling layer），生成一个对数几率 （logits）。NiN 设计的一个优点是，它显著减少了模型所需参数的数量。然而，在实践中，这种设计有时会增加训练模型的时间。



1
2
3
4
5
6
7
8
9
10
11
12
13



net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

GoogLeNet

GoogLeNet 吸收了 NiN 中串联网络的思想，并在此基础上做了改进。 这篇论文的一个重点是解决了什么样大小的卷积核最合适的问题。 毕竟，以前流行的网络使用小到 1×1，大到 11×11 的卷积核。 本文的一个观点是，有时使用不同大小的卷积核组合是有利的。

Inception 块

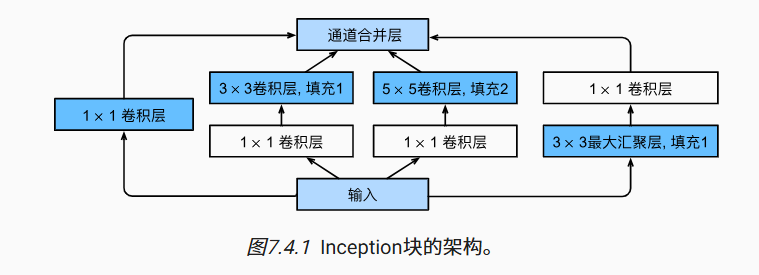
Inception 块由四条并行路径组成。 前三条路径使用窗口大小为 1×1、3×3 和 5×5 的卷积层，从不同空间大小中提取信息。 中间的两条路径在输入上执行 1×1 卷积，以减少通道数，从而降低模型的复杂性。 第四条路径使用 3×3 最大汇聚层，然后使用 1×1 卷积层来改变通道数。 这四条路径都使用合适的填充来使输入与输出的高和宽一致，最后我们将每条线路的输出在通道维度上连结，并构成 Inception 块的输出。在 Inception 块中，通常调整的超参数是每层输出通道数。
1d29c0ad475d66b8ae7304b2b3c0195.png



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28



import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层(1*1卷积为了减少输入通道数，降低复杂性)
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层(1*1卷积为了减少输入通道数，降低复杂性)
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)

GoogLeNet 模型

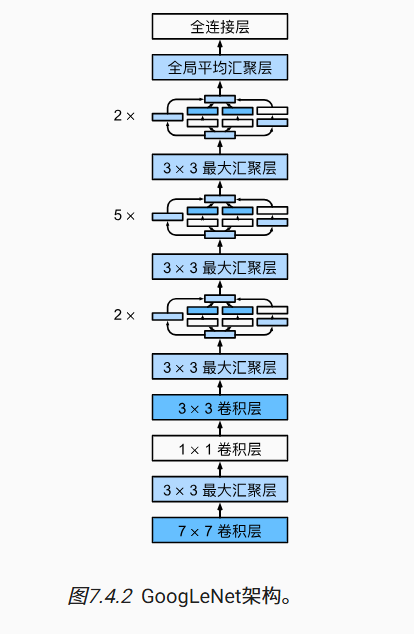
GoogLeNet 一共使用 9 个 Inception 块和全局平均汇聚层的堆叠来生成其估计值。Inception 块之间的最大汇聚层可降低维度。 第一个模块类似于 AlexNet 和 LeNet，Inception 块的组合从 VGG 继承，全局平均汇聚层避免了在最后使用全连接层。
faac7cddd37c187be34cd860dfebb89.png

ResNet（残差网络）

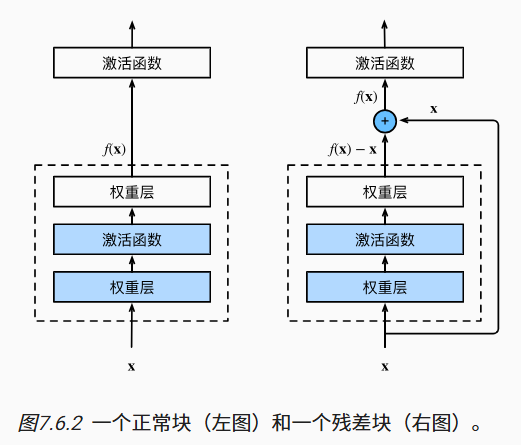
残差网络的核心思想是：每个附加层都应该更容易地包含原始函数作为其元素之一。 于是，残差块（residual blocks）便诞生了，这个设计对如何建立深层神经网络产生了深远的影响。

1c0fb3c40644e1448f7d5b5d5591a36.png

ResNet 沿用了 VGG 完整的 3×3 卷积层设计。 残差块里首先有 2 个有相同输出通道数的 3×3 卷积层。 每个卷积层后接一个批量规范化层和 ReLU 激活函数。 然后我们通过跨层数据通路，跳过这 2 个卷积运算，将输入直接加在最后的 ReLU 激活函数前。 这样的设计要求 2 个卷积层的输出与输入形状一样，从而使它们可以相加。 如果想改变通道数，就需要引入一个额外的 1×1 卷积层来将输入变换成需要的形状后再做相加运算。 残差块的实现如下：

ResNet Block



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28



import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

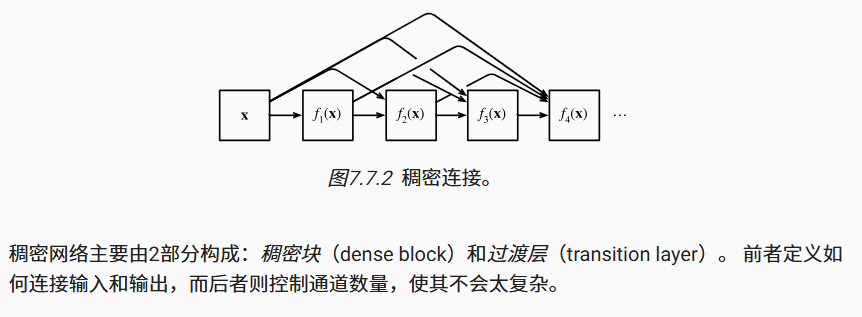
DenseNet(稠密连接网络)

3566d20d6cda6570412cfb4c0c1a813.png

DenseBlock



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24



import torch
from torch import nn
from d2l import torch as d2l

def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))
        
class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(
                num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出
            X = torch.cat((X, Y), dim=1)
        return X

Transition Layer

由于每个稠密块都会带来通道数的增加，使用过多则会过于复杂化模型。 而过渡层可以用来控制模型复杂度。 它通过 1×1 卷积层来减小通道数，并使用步幅为 2 的平均汇聚层减半高和宽，从而进一步降低模型复杂度。



1
2
3
4
5



def transition_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))