2024-06-15-Optimizing Algorithms

Mini-batch Gradient descent

背景

当训练的数据集规模十分庞大时，即使我们采用向量化加速并利用并行计算，进行一次梯度下降的训练耗时依然很高。为了优化算法的执行速度，我们考虑将训练集划分为规模更小的 mini-batch 的集合，在遍历 mini-batch 的过程中实现梯度下降。

实施

1. 分割
   将初始样本集分割为若干个大小一定的 mini-batch,mini batch 的数量为 t

$$\begin{array}{rlr}& X=\left[\begin{array}{c}{x}^{(1)},\dots ,x^{(m)}\end{array}\right]=\left[\begin{array}{c}{x}^1,\dots ,x^t\end{array}\right]& Y=\left[\begin{array}{c}{y}^{(1)},\dots ,y^{(m)}\end{array}\right]=\left[\begin{array}{c}{y}^1,\dots ,y^t\end{array}\right]\end{array}$$

进而，我们有：

$$\begin{array}{rlrlr}& X\in {\mathbb{R}}^{n^x\times m}& x^t\in {\mathbb{R}}^{n^x\times m/t}& Y\in {\mathbb{R}}^{1\times m}& y^t\in {\mathbb{R}}^{1\times m/t}\end{array}$$

1. 原理
   相比与每次执行梯度下降遍历整个大的训练集，采用 mini-batch 的方法，我们每次计算一个 mini-batch 时即可实现一次梯度下降，这个过程也被称为一次 epoch.

梯度下降的步骤与之前在整个训练集上进行完全相同，只是将训练规模减小

分析

Noise in Cost Function Curve

由于我们每次梯度下降所采用的 mini-batch 不同，且单个 mini-batch 无法代表整个训练集的整体情况，所以当我们尝试绘制出 cost function 关于某个 mini-batch 的曲线时会发现曲线并非严格递减，而是会有很多噪声，但整体成递减趋势

参数选择: mini-batch 大小

1. t = 1
   即为完整的batch gradient descent,执行一次迭代所需的时间太长
2. t = m
   即为stochastic gradient descent,一方面由于每次执行的样本集太小导致噪声过大（最终结果也只会在最优值附近震荡），且丧失了向量化带来的并行计算优势
3. 中间情况：
   需选择合适的样本集大小来平衡噪声与训练速度

[!Important] 选择注意事项

• 如果训练集较小，直接采取 batch gradient descent 即可
• 考虑到电脑内存设置，mini-batch 大小最好为 2 的幂次，64-512 比较常见
• 选择的 mini-batch 要符合 CPU,GPU 内存设置

指数加权平均 (Exponentially weighted averages)

原理

$$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$$

核心参数: $\beta$ ,同时将初始估计值设为 0
将递推表达式展开为原始参数的表达式我们可以得到：

$$ v_{t} = \sum_{i=1}^{t}(1-\beta)\beta ^{t-i}\theta_{i} $$

代码中实现:

v  = 0
v := beta*v + (1-beta)*theat_i

这种实现可以大量节省内存

对参数 $\beta$ 理解

$\frac{1}{1-\beta }$ 表示了指数加权平均所表征的数据平均值
原理：

$${\beta }^{1/1-\beta }\text{近似于}\frac{1}{e}$$

所以当我们考察前 $\frac{1}{1-\beta }$ 个数据点对当下的影响时，它的权重为 1/3 左右，我们在此截断

[!Important] $\beta$ 的影响

• 随着 $\beta$ 增大，指数加权平均更趋向于更多数据点的平均值，所绘制出的移动均线更平缓，但对剧烈变化的反应不灵敏
• 随着 $\beta$ 减小，指数加权平均更趋向于更少数据点的平均值，所绘制出的移动均线噪声更多，但对剧烈变化的反应灵敏

偏差修正 (bias correction)

由于我们将加权指数均值的初始值设置为 0，所以这种估计方式在开始阶段存在比较大的误差（开始数据点权重很小），如果我们想要减少偏差，可以采用偏差修正的手段

$$v_t=\frac{v_t}{1-{\beta }^t}$$

优化算法

动量梯度下降 (Gradient Descent With Momentum)

核心想法

通过对 dW 与 db 采用指数加权平均的手段对其进行梯度下降时的更新，从而减缓梯度下降时在纵轴上的波动程度，进而可以考虑采取更大的学习率来加速梯度下降
物理直观：
通过计算指数平均保持之前梯度下降的速度，dw 则充当进行进一步梯度下降的加速度

实现

$$ \begin{align}
& v_{dw} = \beta v_{dw} + (1-\beta)dw
& v_{db} = \beta v_{db} + (1-\beta)dv
&dw = w -\alpha v_{dw}
&db = b - \alpha v_{db} \

\end{align} $$

$\beta$ 的常见取值为 0.9

RMSprop(Root Mean Square Prop)

核心想法

一方面减缓 Cost Function 在梯度下降时在某一个方向的振幅，从而能够使用更高学习率逼近最小值，同时保持另一个方向的学习速度不减

实现

注意下述平方操作均为 element-wise

$$\begin{array}{rlrlr}& S_{dW}=\beta S_{dW}+(1-\beta )d{W}^2& S_{db}=\beta S_{db}+(1-\beta )d{b}^2& dW=W-\alpha \frac{dW}{\sqrt{S_{dW}}}& db=b-\alpha \frac{db}{\sqrt{S_{db}}}\end{array}$$

注意

• 为了与动量梯度下降的 $\beta$ 区分，我们常用 ${\beta }_2$
• 为了保持数值稳定性，我们常在 $S_{dW}\mathrm{或}{S}_{db}$ 中加上小量 $ϵ$ 防止分母为 0

Adam 优化算法

Adaptive Moment Estimation
将动量均值下降与 RMSprop 相结合

实现

初始化：

$$v_{dW}=0,S_{dW}=0,v_{db}=0,S_{db}=0$$

结合动量均值下降与 RMSprop：

$$\begin{array}{rlrlr}& v_{dw}={\beta }_1{v}_{dw}+(1-{\beta }_1)dw& v_{db}={\beta }_1{v}_{db}+(1-{\beta }_1)db& S_{dw}={\beta }_2{S}_{dw}+(1={\beta }_2)d{w}^2& S_{db}={\beta }_2{S}_{db}+(1-{\beta }_2)d{b}^2\end{array}$$

偏差修正：

$$\begin{array}{rlrlr}& v_{dw}^{cor}=\frac{v_{dw}^{cor}}{1-{\beta }_1^t}& S_{dw}^{cor}=\frac{S_{dw}}{1-{\beta }_2^t}& v_{db}^{cor}=\frac{v_{db}}{1-{\beta }_1^t}& S_{db}^{cor}=\frac{S_{db}}{1-{\beta }_2^t}\end{array}$$

将两者结合进行梯度下降:

$$\begin{array}{rlr}& dw=w-\frac{\alpha \ast v_{dw}^{cor}}{\sqrt{S_{dw}^{cor}}+ϵ}& db=b-\frac{v_{db}^{cor}}{\sqrt{S_{db}^{cor}}+ϵ}\end{array}$$

超参数选取

• $\alpha$ 需要在优化时调整
• ${\beta }_1$ 常取 0.9
• ${\beta }_2$ 常取 0.99
• $ϵ$ 不重要

学习率衰减 (learning rate decay)

核心想法

$\alpha$ 应该随着模型迭代次数的增加而缓慢减小，在学习的初期应该选取较大的 $\alpha$ 加快学习速率，在后期选取较小的 $\alpha$ 较小在最小值附近的振荡

实现

有几种常见的公式:

$$ \begin{align} & \alpha = \frac{1}{1+decayrateepoch-num}\alpha_{0}
& \alpha = \frac{k}{\sqrt{ epoch-num }}*\alpha_{0}
& \alpha = 0.95^{epoch-num}\alpha_{0}
& discrete \ decay \end{align} $$

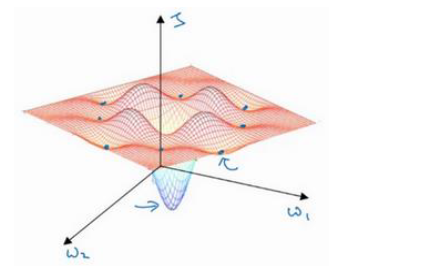
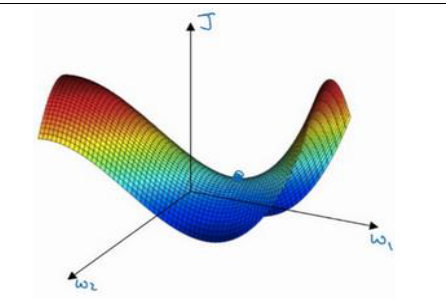
局部最优问题 (The problem of local optima)

人们常用低维空间中的直觉认为 $dw=0\mathrm{或}db=0$ 对应的点为局部最小值，导致无法进行梯度下降。事实上，在高维空间中这样的点是局部最小值的可能性很小，更多的可能是驻点。
Local Optima:

鞍点：