背景

Binary Classification

Logistic regression(逻辑回归) 通常用于处理二分类问题 (binray classification), 在二分类问题中，模型的任务为根据训练数据集给输入的数据集以 0 或 1(或正或负) 等二元标签来分类。

数据处理

将原始的数据转化为可被当前模型容易处理的格式，同时包括向量化 (Vectorization) 与归一化 (Normalization)，前者便于进行并行计算提高计算效率，后者则有利于平衡不同特征对最终权和的影响并通过控制特征值的范围保持数值的稳定性。

以图像处理为例

将一张由 $a * a$ 个像素点的图片利用每个像素的 RGB 值输出一个特征向量 $v$,其中 $v \in \mathbb{R}^{aa3}$ ,我们的目标即为训练出能够接受该向量的模型并给出确定的 0 或 1 作为输出预测。

梯度下降 (Gradient Descent)

前向传播 (Forward Propagation)

总体思路：从已有的训练集出发，建立模型拟合训练集中的结果，并以损失函数形式表述 (loss function).
对于输入值 $x^{i}\in X$($x^{i}\in \mathbb{R}^{n_{x}}$), 我们先尝试构造线性拟合函数如下（参考 linear regression):

$$ z^{i} = w^{T}x^{i} + b $$

其中 $w$ 为权重向量，$b$ 为偏移值 (offset).
但线性拟合函数在二分类问题中表现不佳，我们期望寻找输出值的概率表示（取值在 0 和 1 范围内）-> 采用激活函数 (sigmoid function)

$$ a^{i} = \hat{y^{i}} = sigmoid(z^{i}) = \frac{1}{1+e^{-z^{i}}} $$

再定义损失函数 ($a^{i}$ 或 $\hat{y^{i}}$ 为模型的输出值， $y^{i}$ 为训练集中原本的结果)：

$$ \mathcal{L}(a^{i},y^{i}) = -(y^{i}\log(a^{i}) + (1-y^{i})\log(1-a^{i})) $$

损失函数选取原理 2024-06-12-Loss Function（让损失函数表征我们期望的概率，同时尽可能为凸函数以免出现多个局部最小值）

在以 A 与 J 表示所有训练样本上的模型预测值与损失总和：

$$ \begin{align} &A = (a^{1}, a^{2}, \dots, a^{m}) = \sigma(w^{T}X + b) = \frac{1}{1+e^{-(w^{T}X+b)}}
&J = -\frac{1}{m}\sum_{i=1}^{m}(y^{i}\log(a^{i})+(1-y)^{i}\log(1-a^{i})) \end{align} $$

[!note] Why Sigmoid Function
非线性变化

Sigmoid 函数引入非线性，使得神经网络能够学习和表示复杂的非线性关系。如果没有非线性激活函数，神经网络的所有层的组合将等价于一个单一的线性变换，限制了模型的表达能力。

输出范围

Sigmoid 函数将输入值压缩到 (0, 1) 范围内，这使得它非常适合用于表示概率。对于二分类问题，Sigmoid 函数的输出可以直接用作样本属于某个类别的概率。

梯度平滑

Sigmoid 函数是连续可导的，且其导数也是连续的。这使得在反向传播过程中计算梯度变得简单和稳定，从而有助于优化算法（如梯度下降）更有效地更新模型参数。

生物学

Sigmoid 函数的形状类似于生物神经元的激活函数。它平滑地从 0 过渡到 1，类似于神经元在接收到足够的刺激后从不激活状态过渡到完全激活状态。

反向传播 (Backward Propagation)

在定义完前向传播中我们如何由输入的数据集给出预测的结果后并计算总损失，现在我们在反向传播中利用梯度下降，实现对参数的优化。
初始参数一般选择为 0

梯度下降原理（迭代）

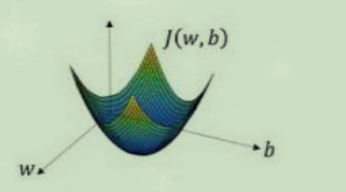
8a8c92257a5641aef235b663b74b0ae.png
从几何直觉上看，梯度下降即为不断利用对凸函数求偏导，寻找到其最快递减的方向，最终接近全局最小值。
迭代过程：

$$ \begin{align} &w := w - a\frac{dJ}{dw}
&b := b - a\frac{dJ}{db} \end{align} $$

其中 a 表示 (learning rate)，用来控制每次梯度下降的步长

求导实现

经过求导，我们不难有 (对于单个样本）：

$$ \begin{align} & \frac{dL}{da} = -\frac{y}{a} + \frac{1-y}{1-a}
& \frac{da}{dz} = a(1-a) \quad \text{(sigmoid函数的性质,可求导验证)}
& \frac{dL}{dz} = \frac{dL}{da} * \frac{da}{dz} = a - y \quad \text{(预测值与训练集中结果之差)}
& \frac{dL}{dw} = (a-y)x
& \frac{dL}{db} = a-y \end{align} $$

向量化 (Vectorization)

对于深度学习模型，我们通常需要处理非常大规模的数据，如果直接采用显示的 for 循环将无法利用并行计算的优势，降低计算效率，所以我们采取向量化的方式来提高计算效率 (利用 numpy 包内置的优化并行计算)
将 m 个样本输入集构造为 $n_{x}*m$ 为的矩阵：

$$ X = [x_{1}, x_{2}, \dots, x_{m}] $$

用 m 个权重构造为 m 维权重向量:

$$ w = \begin{bmatrix} w_{1}
w_{2}
\dots
w_{m}
\end{bmatrix} $$

利用向量 w 与矩阵 X 的点乘我们即可省去对于样本集中每个向量的 for 循环，同时便捷地得出向量 A

经过构造 w,我们也同样实现了对于反向传播过程中分别计算每个维度的权重的向量化。
a63c79e43568efb32347dedce0cf193.png

进一步地，我们将 m 个数据集组合，构造向量 $dZ$ 与 $dw$, $db$

$$ \begin{align} &dZ = [a^{1}-y^{1},\dots,a^{m}-y^{m}] = A -Y
&dw = \frac{1}{m}Xdz^{T}
&db = \frac{1}{m}*\sum_{i=1}^{m}dZ_{i} \end{align} $$

最终梯度下降的迭代式为:

$$ \begin{align} &w := w - adw
&b := b - adb \end{align}

$$

代码实现



1



# Waited to be done

注意

Python 中的广播 (Broadcasting)

Numpy 库自动扩充向量为矩阵简化代码并实现更高效、灵活的操作。
详见：NumPy Array Broadcasting (geeksforgeeks.org)

秩 1 数组

当我们在写 python 程序时避免利用秩 1 数组来构造向量与矩阵，可以利用 reshape 和 assert 来提高代码的稳定性。