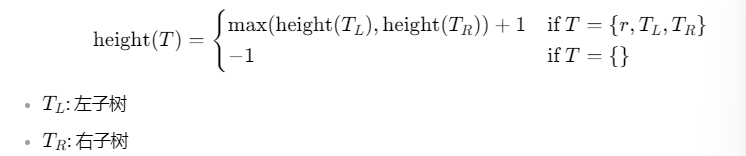Data Structure-2

#CS225

Tree

Concept & Teminology

定义: 树是一种非线性 (non-linear) 数据结构，由节点 (node) 和边 (edge) 组成。
关键特性:
- Acyclic Graph (无环图): 树中不存在环路。
- Connected Graph (连通图): 任意两个节点之间都存在路径。
术语:
- 节点 (Node/Vertex): 树中的每个元素。
- 边 (Edge): 连接两个节点的线。
- 根节点 (Root): 树的顶端节点，没有父节点。
- 父节点 (Parent): 有子节点的节点。
- 子节点 (Child): 被父节点指向的节点。
- 兄弟节点 (Sibling): 拥有相同父节点的节点。
- 路径 (Path): 从一个节点到另一个节点经过的边的序列。
- 叶子节点 (Leaf): 没有子节点的节点。
- 子树 (Subtree): 树中的任意节点及其所有后代。
- 祖先 (Ancestor): 从根节点到某个节点路径上的所有节点。
- 后代 (Descendant): 某个节点子树中的所有节点。
- 高度 (Height): 从根节点到最远叶子节点的最长路径 (longest path) 上的边的数量 (Count Edges)。

二叉树及基本性质

定义: 二叉树 (Binary Tree) 是一种特殊的树，其中每个节点最多有两个子节点，分别称为左子节点 (left child) 和右子节点 (right child)。
性质:
- 满二叉树 (Full Binary Tree): 每个节点要么没有子节点，要么有两个子节点。
- 完美二叉树 (Perfect Binary Tree): 所有内部节点都有两个子节点，并且所有叶子节点都在同一层。高度为 h 的完美二叉树的节点数量: $2^{h + 1} - 1$
- 完全二叉树 (Complete Binary Tree): 除了最后一层，其他每一层都是满的，并且最后一层的节点都尽可能地靠左排列。

template <class T>
class BinaryTree {
private:
    struct TreeNode {
        T data;
        TreeNode *left;
        TreeNode *right;
    };

    TreeNode *root;

public:
    BinaryTree() : root(nullptr) {} // 构造函数
    ~BinaryTree() { clear(); }      // 析构函数，释放内存

    // ... (其他方法，例如 insert, remove, traverse 等) ...
};

1. Height

定义：

从根节点到最远叶子节点的最长路径 (longest path) 上的边的数量 (Count Edges)。
- 空树的高度是 -1。
- 只有一个节点的树的高度是 0。

递归定义：

2. Full Tree
每个节点要么没有子节点，要么有两个子节点

$F =$ 空树为满二叉树
$F = r, T_{L}, T_{R}$ 其中 $T_{L}, T_{R}$ 要么都为空，要么都不为空

3. Perfect Tree
所有内部节点都有两个子节点，并且所有叶子节点都在同一层
高度为 h 的完美二叉树的节点数量: $P_{h} = 2^{h + 1} - 1$

递归定义：

$P =$
$P = r, T_{L}, T_{R}$ 其中 $T_{L}, T_{R}$ 高度均为 $h - 1$

4. Complete Tree
除了最后一层，其他每一层都是满的，并且最后一层的节点都尽可能地靠左排列。

递归定义：对于高度为 h 的完全二叉树 $C_{h}$ :
1. $C_{- 1} =$ (空树是高度为 -1 的完全二叉树)
2. $C_{h} = r, T_{L}, T_{R}$ , 并且满足以下条件之一：
  - $T_{L} 是 C_{h - 1}$ ， $T_{R} 是 P_{h - 2}$
  - $T_{L} 是 P_{h - 1}$ , $T_{R} 是 C_{h - 1}$
  - P: 完美二叉树 (perfect binary tree)
  - C: 完全二叉树 (complete binary tree)
  - 下标表示树的高度

[!warning] 注意

满二叉树不一定是完全二叉树

完全二叉树不一定是满二叉树

5. NULL 的数量

NULL 的数量为当前节点数量 +1（可以利用数学归纳法证明）

Abstract Data Type(ABT)

Insert

template <class T>
void BinaryTree<T>::insert(T value) {
    TreeNode *newNode = new TreeNode{value, nullptr, nullptr};

    if (!root) {
        root = newNode;
        return;
    }

    TreeNode *current = root;
    while (current) {
        if (value < current->data) {
            if (!current->left) {
                current->left = newNode;
                return;
            }
            current = current->left;
        } else {
            if (!current->right) {
                current->right = newNode;
                return;
            }
            current = current->right;
        }
    }
}

Remove

template <typename T>
void Tree<T>::remove(TreeNode<T>* node) {
    if (node == nullptr) return;
    
    // 获取父节点引用
    TreeNode<T>* parent = node->parent;
    
    // 处理节点是根节点的情况
    if (parent == nullptr) {
        // 根节点删除操作
        delete_subtree(root);
        root = nullptr;
        return;
    }
    
    // 处理一般情况
    // 1. 更新父节点的子节点链表
    if (parent->firstChild == node) {
        // 如果是第一个子节点
        parent->firstChild = node->nextSibling;
    } else {
        // 如果不是第一个子节点，需要遍历找到前一个兄弟节点
        TreeNode<T>* sibling = parent->firstChild;
        while (sibling != nullptr && sibling->nextSibling != node) {
            sibling = sibling->nextSibling;
        }
        
        if (sibling != nullptr) {
            sibling->nextSibling = node->nextSibling;
        }
    }
    
    // 2. 递归删除子树
    delete_subtree(node);
}
// 删除子树的辅助函数
template <typename T>
void Tree<T>::delete_subtree(TreeNode<T>* node) {
    if (node == nullptr) return;
    
    // 递归删除所有子节点
    TreeNode<T>* child = node->firstChild;
    while (child != nullptr) {
        TreeNode<T>* next = child->nextSibling;
        delete_subtree(child);
        child = next;
    }
    
    // 删除当前节点
    delete node;
}

Copy

template<class T>
TreeNode * BinaryTree<T>::copy_(TreeNode* root){
	if (root != nullptr){
		TreeNode* t = new TreeNode(root->data);
		t->left = copy_(root->left);
		t->right = copy_(root->right);
	}
	return t;
}

Clear

template<class T>
void BinaryTree<T>::clear_(TreeNode* root){
	if(root != nullptr){
		clear_(root->left);
		clear_(root->right);
		delete root;
		}
}

Traversal

Depth-First 深度优先遍历

1. 前序遍历（Pre-order Traversal）
先访问根节点，然后递归地前序遍历左子树，最后递归地前序遍历右子树。

2. 中序遍历（In-order Traversal）
先递归地中序遍历左子树，然后访问根节点，最后递归地中序遍历右子树。

3. 后续遍历（Post-order Traversal）
先递归地后序遍历左子树，然后递归地后序遍历右子树，最后访问根节点。

template <class T>
void BinaryTree<T>::preOrder(TreeNode *root) {
    if (root != NULL) {
        std::cout << root->data << " "; // 访问根节点
        preOrder(root->left);           // 递归遍历左子树
        preOrder(root->right);          // 递归遍历右子树
    }
}

template <class T>
void BinaryTree<T>::inOrder(TreeNode *root) {
    if (root != NULL) {
        inOrder(root->left);            // 递归遍历左子树
        std::cout << root->data << " "; // 访问根节点
        inOrder(root->right);           // 递归遍历右子树
    }
}

template <class T>
void BinaryTree<T>::postOrder(TreeNode *root) {
    if (root != NULL) {
        postOrder(root->left);           // 递归遍历左子树
        postOrder(root->right);          // 递归遍历右子树
        std::cout << root->data << " "; // 访问根节点
    }
}

Level-order Traversal 层序遍历

按照树的层次，从上到下，从左到右逐层访问节点。
实现方法：通常使用队列（Queue）来实现。
算法步骤：
1. 将根节点放入队列。
2. 当队列不为空时，执行以下操作： a. 取出队列的头节点并访问。 b. 如果该节点有左子节点，将左子节点放入队列。 c. 如果该节点有右子节点，将右子节点放入队列。

template <class T>
void BinaryTree<T>::levelOrder(TreeNode *root) {
    std::queue<TreeNode *> q;
    q.enqueue(root);
    while (!q.isEmpty()) {
        TreeNode *node = q.dequeue();
        if (node != NULL) {
            std::cout << node->data << " ";
            if (node->left)
                q.enqueue(node->left);
            if (node->right)
                q.enqueue(node->right);
        }
    }
}

Breadth First V.S. Depth First

[!tip] Traversal 与 Search
Traversal: 遍历每一个节点一次
Search: 访问每个节点直到我们找到一个或多个满足要求的节点

特性	BFS	DFS
数据结构	队列 (Queue)	栈 (Stack)
访问顺序	按层级	按深度
空间复杂度	可能更高 (需存储整层顶点)	通常较低
适用场景	寻找最短路径、关系网络分析	拓扑排序、连通性检测
实现难度	稍微复杂	相对简单

Binary Search Tree

Definition

基本定义: BST 是一种特殊的二叉树 (Binary Tree)，它或者为空，或者满足以下递归属性：
- 每个节点包含一个键 (Key) 和关联的值 (Value)。
- 对于树中的任意节点 r：
  - 其左子树 (Left Subtree) TL 中所有节点的键都小于节点 r 的键。
  - 其右子树 (Right Subtree) TR 中所有节点的键都大于节点 r 的键。
  - 其左子树 TL 和右子树 TR 本身也必须是二叉搜索树。
核心目的: 利用这种有序属性，实现高效的查找、插入和删除操作。

性能分析

最佳情况 (Best Case):
- 当树是平衡 (Balanced) 的时候 (例如，形状接近完美二叉树 Perfect Binary Tree 或完全二叉树 Complete Binary Tree)，树的高度 h 大约是 $h \approx O (\log n)$ ，其中 $n$ 是节点数。
- 查找、插入、删除操作的时间复杂度为 $O (\log n)$ 。
最坏情况 (Worst Case):
- 当插入的元素是有序的 (或接近有序) 时，BST 会退化成一个链表 (Linked List) 结构。
- 树的高度 h 变为 $O (n)$ 。
- 查找、插入、删除操作的时间复杂度变为 $O (n)$ 。
结论: BST 的效率高度依赖于其结构是否平衡，即依赖于元素的插入顺序。这也引出了后续更高级的自平衡 BST (如 AVL 树, Red-Black Tree) 的需求。

具体实现

节点结构 (TreeNode): 通常使用一个结构体或类来表示节点。

template <class K, class V>
struct TreeNode {
    K key;
    V value;
    TreeNode* left;
    TreeNode* right;

    // Constructor with initializer list
    TreeNode(const K& newKey, const V& newValue)
        : key(newKey), value(newValue), left(nullptr), right(nullptr) {}
};

key, value: 存储键和值。
left, right: 指向左右子节点的指针 (Pointer)。使用 nullptr 表示没有子节点。
模板 (Template) (template <class K, class V>): 使 BST 可以存储任意类型的键和值。

BST 类骨架:

template <class K, class V>
class BST {
public:
    // Constructor, Destructor, etc.
    BST();
    ~BST(); // Important for memory management!

    // Public interface functions
    void insert(const K& key, const V& value);
    V find(const K& key) const;
    void remove(const K& key);
    // ... other functions like traverse ...

private:
    TreeNode<K, V>* root; // Pointer to the root node

    // Private recursive helper functions
    // Note the use of TreeNode*& for modification
    TreeNode<K, V>*& find(TreeNode<K, V>*& subroot, const K& key); // Non-const version for internal use
    const TreeNode<K, V>* find(const TreeNode<K, V>* subroot, const K& key) const; // Const version for public find
    void insert(TreeNode<K, V>*& subroot, const K& key, const V& value);
    void remove(TreeNode<K, V>*& subroot, const K& key);
    // ... other helpers like finding successor/predecessor, clear/destroy ...

    // Helper for finding inorder successor (example for remove)
    TreeNode<K, V>*& inorderSuccessor(TreeNode<K, V>*& node);
};

root: 指向树根节点的私有成员指针。
公共接口 (Public Interface): 提供给用户的简洁函数 (如 insert(key, value))。
私有辅助函数 (Private Helpers): 通常是递归函数，处理实际的树操作。它们经常使用 TreeNode*& 参数来实现对树结构的修改。

BST 操作与 C++ 实现思路

查找 (Find):

逻辑: 从根节点开始，比较目标键 key 与当前节点 subroot->key：
1. 相等: 找到。
2. key < subroot->key: 递归在左子树 subroot->left 中查找。
3. key > subroot->key: 递归在右子树 subroot->right 中查找。
4. subroot == nullptr: 未找到。

C++ (Const Helper):

template <class K, class V>
const TreeNode<K, V>* BST<K, V>::find(const TreeNode<K, V>* subroot, const K& key) const {
    if (subroot == nullptr) {
        return nullptr; // Base case: Not found
    }
    if (key == subroot->key) {
        return subroot; // Base case: Found
    } else if (key < subroot->key) {
        return find(subroot->left, key); // Recurse left
    } else {
        return find(subroot->right, key); // Recurse right
    }
}
// Public interface would call this helper starting from root
// and likely return V (the value) or throw an exception if not found.

注意: 用于 insert/remove 的内部 find 变体可能需要返回 TreeNode*& 并且是非 const 的。

插入 (Insert):

逻辑: 类似查找，递归向下直到找到一个 nullptr 的链接 (即合适的叶子位置)，然后将新节点连接到该位置。

C++ (Helper using TreeNode*&):

template <class K, class V>
void BST<K, V>::insert(TreeNode<K, V>*& subroot, const K& key, const V& value) {
    if (subroot == nullptr) {
        // Found the insertion spot! Modify the pointer (passed by reference)
        subroot = new TreeNode<K, V>(key, value);
    } else if (key < subroot->key) {
        insert(subroot->left, key, value); // Recurse left
    } else if (key > subroot->key) {
        insert(subroot->right, key, value); // Recurse right
    }
    // else key == subroot->key: Handle duplicate keys (e.g., ignore, update value, throw error)
}
// Public interface calls: insert(root, key, value);

关键: subroot = new TreeNode(...) 之所以能修改树结构，是因为 subroot 是 TreeNode*& (指针的引用)。

删除 (Remove):

中序前驱 (In-order Predecessor, IOP):
* 定义: 在中序遍历序列中，紧接在当前节点之前的那个节点。
* 查找方法: 从当前节点的左子节点开始，一直向右走到底。
* 关键属性: IOP 节点本身最多只有一个左子节点 (绝对没有右子节点)。这保证了递归删除 IOP 时只会遇到 Case 1 或 Case 2。
中序后继 (In-order Successor, IOS): (另一种可选策略)
- 定义: 在中序遍历序列中，紧接在当前节点之后的那个节点。
- 查找方法: 从当前节点的右子节点开始，一直向左走到底。
- 关键属性: IOS 节点本身最多只有一个右子节点 (绝对没有左子节点)。
实现选择: 可以选择使用 IOP 或 IOS。下面的代码示例使用了 IOP。
目标: 从 BST 中删除一个键为 key 的节点，并保持 BST 属性。这是 BST 操作中最复杂的一个。
核心挑战: 删除节点后，如何重新连接子树以维持 BST 结构。
类型：1. 无叶子节点 2. 有一个叶子节点 3. 有两个叶子节点
C++ 接口与辅助函数:

```cpp // Public interface template <class K, class V> void BST<K, V>::remove(const K& key) { remove(root, key); // Call private helper }

// Private recursive helper function (using reference to pointer)
template <class K, class V>
void BST<K, V>::remove(TreeNode<K, V>*& subroot, const K& key) {
    if (subroot == nullptr) {
        return; // Key not found, nothing to remove
    }

    // Step 1: Find the node to remove
    if (key < subroot->key) {
        remove(subroot->left, key); // Recurse left
    } else if (key > subroot->key) {
        remove(subroot->right, key); // Recurse right
    } else {
        // Step 2: Node found (key == subroot->key). Handle the three cases.

        // Case 1: Leaf Node (0 children)
        // "leaf element, no child, very easy"
        if (subroot->left == nullptr && subroot->right == nullptr) {
            delete subroot;
            subroot = nullptr; // The parent's pointer (via reference) is now null
            
        // Case 2: One Child
        // "Remove in a linked list", "one child"
        // Only right child exists
        else if (subroot->left == nullptr) {
            TreeNode<K, V>* temp = subroot; // Store node to delete
            subroot = subroot->right;      // Bypass: parent points to the right child
            delete temp;                   // Delete the original node
        }
        // Only left child exists
        else if (subroot->right == nullptr) {
            TreeNode<K, V>* temp = subroot; // Store node to delete
            subroot = subroot->left;       // Bypass: parent points to the left child
            delete temp;                   // Delete the original node
        }

        // Case 3: Two Children
        // "How to arrange the children??" -> Use In-order Predecessor (IOP)
        else {
            // 3a. Find the In-order Predecessor (IOP)
            // IOP: "far right node in the left subtree"
            // Find the pointer *to* the IOP node itself
            TreeNode<K, V>* iopNode = subroot->left; // Start in the left subtree
            while (iopNode->right != nullptr) {
                iopNode = iopNode->right; // Go as far right as possible
            }
            // Note: Slides 9-11 correctly state IOP has 0 or 1 child (never a right child)

            // 3b. Copy IOP's data to the node we intended to remove (Conceptual "Swap")
            // We replace the data in `subroot` with the data from `iopNode`.
            // This preserves the BST structure locally around `subroot`.
            subroot->key = iopNode->key;
            subroot->value = iopNode->value;

            // 3c. Recursively remove the original IOP node - Slides 16-18
            // Now, the problem reduces to removing the IOP node (which contains the copied data)
            // from the *left subtree*. Since the IOP has 0 or 1 child,
            // this recursive call will hit Case 1 or Case 2.
            remove(subroot->left, iopNode->key); // Remove the IOP from the left subtree
        }
    }
}
```

BST 复杂度分析

基本原则: 所有主要的 BST 操作 (find, insert, delete) 的时间复杂度都依赖于树的高度 (Height) h。复杂度为 $O (h)$ 。
树的高度与节点数的关系:
- 设 n 为节点数，h 为树的高度。
- 最佳情况 (Best Case - Balanced Tree):
  - 树的结构尽可能“茂密”，接近完美二叉树。
  - 节点数 $n$ 最多为 $2^{h + 1} - 1$ 。
  - 反解得到高度 $h$ 的下界 (Lower bound): $h \geq ⌊ \log_{2} n ⌋$ ，即 $h = Ω (\log n)$ 。
- 最坏情况 (Worst Case - Degenerate Tree):
  - 树退化成链表。
  - 节点数 $n$ 最少可以只构成高度 $h = n - 1$ 的树 (只有一个节点时 h=0)。
  - 高度 $h$ 的上界 (Upper bound): $h \leq n - 1$ ，即 $h = O (n)$ 。
插入顺序的影响:
- BST 的最终高度严重依赖于键的插入顺序。
  - 例如，按顺序插入 1, 2, 3, 4, 5, 6, 7 会导致 $O (n)$ 的高度。
  - 插入 4, 2, 6, 1, 3, 5, 7 会得到更平衡的树，高度接近 $O (\log n)$ 。
- 对于 n 个不同的键，存在 $n!$ 种可能的插入顺序。
平均情况 (Average Case - Random Insertions):
- 如果我们假设所有 $n!$ 种插入顺序是等概率的 (即随机插入)，那么 BST 的平均高度 (期望高度) 被证明是 $O (\log n)$ 。
- 技术比喻: 虽然可能运气很差构造出一条长链，但“平均来说”，随机插入更倾向于产生相对平衡的树。
运行时间总结 (Slides 30-31):

Operation	BST Average Case	BST Worst Case	Sorted Array	Sorted List
`find`	$O (\log n)$	$O (n)$	$O (\log n)$	$O (n)$
`insert`	$O (\log n)$	$O (n)$	$O (n)$	$O (n)$
`delete`	$O (\log n)$	$O (n)$	$O (n)$	$O (n)$
`traverse`	$O (n)$	$O (n)$	$O (n)$	$O (n)$

对于 Sorted List:
- insert/delete 如果给定位置 (例如，你知道要插入/删除的节点的指针/迭代器)，操作本身是 O(1) (假设是双向链表)。
- 但如果需要先查找元素 (Arbitrary insert/delete)，查找时间是 O(n)，所以整体是 O(n)。
Sorted Array 的 insert/delete 是 O(n) 因为需要移动元素来保持有序。find 可以用二分查找 O(logn)。

Rotation

Height-balanced Tree

高度平衡的定义

高度平衡（Height balance）：对于每一个节点，其左子树的高度和右子树的高度之差的绝对值不超过 1。
- 平衡因子（balance factor）： $b = h e i g h t (T_{R}) - h e i g h t (T_{L})$ ，其中 $T_{R}$ 是右子树， $T_{L}$ 是左子树。
- 如果一棵树是高度平衡的，则对于每个节点， $- 1 \leq b \leq 1$ 。
举例：
- “mountain” 形状的树通常更平衡，而 “stick” 形状的树则不平衡。
- 这就像在跷跷板上保持平衡，两边的重量要尽可能接近。

Rotation

1. 旋转的目的

保持 BST 的性质：旋转操作不能破坏 BST 的有序性。
调整树的平衡：通过旋转，将 “stick” 形状的树转换为 “mountain” 形状的树，使其更加平衡。

2. 旋转的种类

左旋（Left Rotation）：将一个节点的右子节点提升为父节点，原父节点变为左子节点。
右旋（Right Rotation）：将一个节点的左子节点提升为父节点，原父节点变为右子节点。

3. 旋转的步骤 (以右旋为例)

找到不平衡的节点：从底向上找到第一个平衡因子绝对值大于 1 的节点。
确定旋转类型：根据不平衡节点的子树结构，确定需要进行哪种旋转。

核心旋转操作

我们先定义两个基本的旋转操作：左旋和右旋。

1. 右旋 (Right Rotation)

当节点 z 的左子树 (y) 比右子树过高，并且不平衡是由插入到 y 的左子树 (x) 中引起的时 (即 Left-Left Case)，通常执行右旋。

目标：将 y 提升为子树的新根，z 成为 y 的右子节点。

图示：

      z              y
     / \            / \
    y   T4  ===>   x   z      (围绕 z 进行右旋)
   / \           / \   / \
  x   T3        T1 T2  T3 T4
 / \
T1  T2

z: 不平衡的节点。
y: z 的左子节点。
x: y 的左子节点 (导致不平衡的插入路径上的节点)。
T1, T2, T3, T4: 代表可能的子树 (可能是 NULL)。

操作步骤：

y 的右子树 (T3) 成为 z 的新的左子树。
z 成为 y 的新的右子节点。
y 成为原 z 位置的新根节点。

伪代码/C++ 代码 (假设节点结构包含 left, right, height 成员)：

struct Node {
    int key;
    Node *left;
    Node *right;
    int height;
    // Constructor...
};

// Helper function to get height (handles NULL nodes)
int height(Node* N) {
    if (N == nullptr)
        return -1; // 或者 0, 取决于高度定义 (空树高度为-1 或 叶子节点高度为0)
                   // 这里假设空树高度为 -1, 叶子节点高度为 0
    return N->height;
}

// Helper function to update height of a node
void updateHeight(Node* N) {
    if (N != nullptr) {
        N->height = 1 + std::max(height(N->left), height(N->right));
    }
}

// 执行右旋操作
// 输入: z - 需要围绕其进行右旋的节点 (不平衡节点)
// 返回: 旋转后子树的新根节点 (y)
Node* rightRotate(Node* z) {
    Node* y = z->left;       // y 是 z 的左孩子
    Node* T3 = y->right;     // T3 是 y 的右子树

    // 执行旋转
    y->right = z;            // z 成为 y 的右孩子
    z->left = T3;            // T3 成为 z 的左孩子

    // 更新高度 (必须先更新 z, 再更新 y, 因为 y 的高度依赖于更新后的 z)
    updateHeight(z);
    updateHeight(y);

    // 返回新的根节点
    return y;
}

现实比喻：想象 z 是一个枢轴，你抓住 y 向上推，z 就顺时针旋转下来成为 y 的右边部分，而原来夹在 y 和 z 之间的 T3 就挂在了 z 的左边空位上。

2. 左旋 (Left Rotation)

当节点 z 的右子树 (y) 比左子树过高，并且不平衡是由插入到 y 的右子树 (x) 中引起的时 (即 Right-Right Case)，通常执行左旋。

目标：将 y 提升为子树的新根，z 成为 y 的左子节点。

图示：

      z             y
     / \           / \
    T1  y   ===>  z   x       (围绕 z 进行左旋)
       / \       / \ / \
      T2  x     T1 T2 T3 T4
         / \
        T3 T4

z: 不平衡的节点。
y: z 的右子节点。
x: y 的右子节点 (导致不平衡的插入路径上的节点)。
T1, T2, T3, T4: 代表可能的子树 (可能是 NULL)。

操作步骤：

y 的左子树 (T2) 成为 z 的新的右子树。
z 成为 y 的新的左子节点。
y 成为原 z 位置的新根节点。

伪代码/C++ 代码：

// 执行左旋操作
// 输入: z - 需要围绕其进行左旋的节点 (不平衡节点)
// 返回: 旋转后子树的新根节点 (y)
Node* leftRotate(Node* z) {
    Node* y = z->right;      // y 是 z 的右孩子
    Node* T2 = y->left;      // T2 是 y 的左子树

    // 执行旋转
    y->left = z;             // z 成为 y 的左孩子
    z->right = T2;           // T2 成为 z 的右孩子

    // 更新高度 (先更新 z, 再更新 y)
    updateHeight(z);
    updateHeight(y);

    // 返回新的根节点
    return y;
}

现实比喻：与右旋相反，抓住 y 向上推，z 逆时针旋转下来成为 y 的左边部分，原来夹在 z 和 y 之间的 T2 挂在了 z 的右边空位上。

当插入路径形成 “zig-zag” 形状时，需要进行两次旋转。

3. 左右旋 (Left-Right Rotation, LR)

当节点 z 的左子树 (y) 比右子树过高，但！不平衡是由插入到 y 的右子树 (x) 中引起的时 (即 Left-Right Case)。形状像一个 “<”。

目标：将 x 提升为子树的新根。

图示：

      z               z             x
     / \             / \           / \
    y   T4  -(L@y)-> x   T4 -(R@z)-> y   z      (先对 y 左旋, 再对 z 右旋)
   / \             / \         / \ / \
  T1  x           y   T3       T1 T2 T3 T4
     / \         / \
    T2 T3       T1 T2

操作步骤：

先对 z 的左子节点 y 进行一次左旋 (Left Rotation)。这会将 LR 情况转化为 LL 情况。
再对不平衡节点 z 进行一次右旋 (Right Rotation)。

伪代码/C++ 代码：

// 执行左右旋操作
// 输入: z - 不平衡节点
// 返回: 旋转后子树的新根节点 (x)
Node* leftRightRotate(Node* z) {
    // 1. 对 z 的左孩子 y 进行左旋
    z->left = leftRotate(z->left); // y 被 x 替换, 返回的新根 x 成为 z 的新左孩子

    // 2. 对 z 进行右旋
    return rightRotate(z);         // 返回最终的新根 x
}

现实比喻：想象 < 形状的链条，先把它掰直 (对 y 左旋，变成 / 形状，即 LL)，然后再整体旋转 (对 z 右旋) 使其平衡。

4. 右左旋 (Right-Left Rotation, RL)

当节点 z 的右子树 (y) 比左子树过高，但！不平衡是由插入到 y 的左子树 (x) 中引起的时 (即 Right-Left Case)。形状像一个 “>”。

目标：将 x 提升为子树的新根。

图示：

       z              z              x
      / \            / \            / \
     T1  y -(R@y)-> T1  x  -(L@z)-> z   y      (先对 y 右旋, 再对 z 左旋)
        / \            / \        / \ / \
       x   T4         T2  y      T1 T2 T3 T4
      / \                / \
     T2 T3              T3 T4

操作步骤：

先对 z 的右子节点 y 进行一次右旋 (Right Rotation)。这会将 RL 情况转化为 RR 情况。
再对不平衡节点 z 进行一次左旋 (Left Rotation)。

伪代码/C++ 代码：

// 执行右左旋操作
// 输入: z - 不平衡节点
// 返回: 旋转后子树的新根节点 (x)
Node* rightLeftRotate(Node* z) {
    // 1. 对 z 的右孩子 y 进行右旋
    z->right = rightRotate(z->right); // y 被 x 替换, 返回的新根 x 成为 z 的新右孩子

    // 2. 对 z 进行左旋
    return leftRotate(z);          // 返回最终的新根 x
}

现实比喻：想象 > 形状的链条，先把它掰直 (对 y 右旋，变成 \ 形状，即 RR)，然后再整体旋转 (对 z 左旋) 使其平衡。

总结

旋转的目的：在保持 BST 性质的前提下，调整树的局部结构以恢复平衡。
基本操作：左旋和右旋是基础，时间复杂度为 $O (1)$ 。
四种情况：
- LL (Left-Left): 右旋 z。
- RR (Right-Right): 左旋 z。
- LR (Left-Right): 先左旋 y (即 z->left)，再右旋 z。
- RL (Right-Left): 先右旋 y (即 z->right)，再左旋 z。
关键点：
- 正确识别不平衡节点 z 和导致不平衡的路径 (x, y)。
- 精确地更新节点的 left, right 指针。
- 非常重要：在每次旋转后，必须更新受影响节点 (z, y, 可能还有 x) 的高度信息，否则后续的平衡判断会出错。

Dictionary ADT

Dictionary（字典）是一种关联式容器，存储键值对。

主要操作：

put(key, value) - 插入/更新键值对
get(key) - 根据键检索值
remove(key) - 删除键值对
containsKey(key) - 检查键是否存在
size() - 返回字典中的键值对数量
isEmpty() - 检查字典是否为空
keys() - 返回所有键的集合

Tree

Concept & Teminology

二叉树及基本性质

Abstract Data Type(ABT)

Insert

Remove

Copy

Clear

Traversal

Depth-First 深度优先遍历

Level-order Traversal 层序遍历

Breadth First V.S. Depth First

Binary Search Tree

Definition

性能分析

具体实现

BST 操作与 C++ 实现思路

BST 复杂度分析

Rotation

Height-balanced Tree

Rotation

核心旋转操作

1. 右旋 (Right Rotation)

2. 左旋 (Left Rotation)

3. 左右旋 (Left-Right Rotation, LR)

4. 右左旋 (Right-Left Rotation, RL)

总结

Dictionary ADT

主要操作：

反向链接：