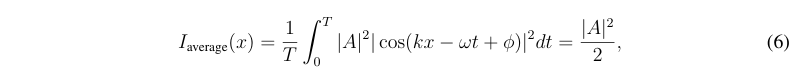PHYS214汇总

table date
from #PHYS214 
sort date

Midterm 1

1. 简谐波
简谐波：

$$y(x,t)=A\cos (kx-\omega t+\varphi )$$

基本参数与转化：

$$\begin{array}{rlrlr}& k=\frac{2\pi }{\lambda }\text{ 描述波在空间上重复的速率}& \omega =2\pi f& T=\frac{1}{f}& v=\frac{\omega }{k}=\lambda f(\mathrm{描}\mathrm{述}\mathrm{波}\mathrm{传}\mathrm{递}\mathrm{的}\mathrm{速}\mathrm{率}，\mathrm{波}\mathrm{长}\mathrm{除}\mathrm{以}\mathrm{周}\mathrm{期})\end{array}$$

振幅与光强：

2. 波的叠加与相位图

• 同振幅同波长
• 波的叠加：

$$\begin{array}{rlrl}& y_1(x,t)=A\cos (kx-\omega t+{\varphi }_1)& y_2(x,t)=A\cos (kx-\omega t+{\varphi }_2)& y_{total}(x,t)=y_1(x,t)+y_2(x,t)=2A\cos \left(\frac{{\varphi }_1-{\varphi }_2}{2}\right)\cos (kx-\omega t+\left(\frac{{\varphi }_1+{\varphi }_2}{2}\right))\end{array}$$

核心影响因素为相位差：波程差 + 初相位差

1. 波程差导致： $k\mathrm{\Delta }x=\frac{2\pi }{\lambda }\mathrm{\Delta }x$
2. 初相位差： ${\varphi }_1-{\varphi }_2$

• 相量图
  核心为考虑复数在二维空间中的叠加（正交或余弦均可）
  对于振幅为 $A_1,A_2$, 相位差为 $\varphi$ 的波的叠加

$$I=\frac{1}{2}{A}^2=\frac{1}{2}(A_1^2+A_2^2-2A_1{A}_2\cos (\pi -\varphi ))=I_1+I_2-2\sqrt{I_1{I}_2}\cos (\pi -\varphi )$$

3. 双缝干涉
干涉考虑相位差的来源：

• 波程差： $\mathrm{\Delta }x=d\sin {\theta }_m$ ， $d$ 为两缝间距
  当光程差为波长的整数倍时发生相长干涉；为 $\frac{1}{2}$ 个波长加整数时为相消干涉
  相长干涉:

$$\mathrm{\Delta }x=m\lambda$$

相消干涉：

$$\mathrm{\Delta }x=(m+\frac{1}{2})\lambda$$

各个峰或谷的位置: $y=L\tan \theta$
经过近似可以推导得到各个相长干涉的位置：

$$y_m=m\frac{L\lambda }{d}$$

4. 单缝衍射
将狭缝中的每一个点均视为波源
相消衍射 ->各波源矢量分布在完整的圆上
先考虑使光强为 0 的角度 ${\theta }_0$ ，确定光斑大小

• 考虑将宽度为 a 单缝建模为由 N 个点光源组成，其中点光源之间的间距为 $d=\frac{a}{N}$ , 考虑 $N\to \mathrm{\infty }$ 的情况
• 然后计算相消干涉 ->即所有的向量相加和为 0->这些向量均匀排布在单位圆上
• 相邻两者相差相位为 $\frac{2\pi m}{N}$

$$k(r_2-r_1)=\frac{2\pi m}{N}$$

其中 $r_2-r_1=\frac{a}{N}\sin {\theta }_0$,推出

$$a\sin {\theta }_0=m\lambda$$

则

$$y_0=L\tan {\theta }_0$$

相长干涉 ->各波源矢量叠加后为圆的直径

$$a\sin {\theta }_0=(m+\frac{1}{2})\lambda$$

光强推导： $\beta =\frac{\varphi }{2}$

$$I=I_0(\frac{\sin \beta }{\beta }{)}^2$$

5. 圆孔衍射
推导过程与单缝类似，对于直径为 $D$ 的圆孔，需满足的条件为

$$D\sin {\theta }_0=1.22\lambda$$

6. 干涉仪
核心即为波程差为一边移动距离的两倍

$$\mathrm{\Delta }r=2(L_1-L_2)$$

7. 天文望远镜
一般思路：

• 利用星体之间的距离 + 星体到望远镜距离 -> 确定两星体之间的分割角
• 利用圆孔衍射确定产生的衍射光斑的大小，要求衍射光斑不影响各自成像
  注意题目特殊要求
• 透镜直径是否受其他条件限制

8. 光子

• 光子的能量

$$E=hf$$

• 光子的动量

$$p=\frac{h}{\lambda }$$

使电子挣脱金属束缚溢出 ->需达到 threshold

$$E_{initial}=hf-\mathrm{\Phi }\text{ 其中 }\mathrm{\Phi }\text{ 为工作函数}$$

$\mathrm{\Phi }$ 表征材料内部电子的势能

$$E_{final}=K{E}_{electron}$$

Midterm2

1. 波函数与概率密度
我们将粒子的状态用波函数描述，波函数是一个特定时间下关于位置的函数，其值为复数

$$\rho (x)=|\mathrm{\Phi }(x){|}^2={\mathrm{\Phi }}^{\ast }(x)\mathrm{\Phi }(x)$$

当位置 $a<x<b$ 时，根据上述由波函数推导出的概率函数我们有

$$P(a<x<b)={\int }_a^b\rho (x)dx={\int }_a^b{\mathrm{\Phi }}^{\ast }(x)\mathrm{\Phi }(x)dx$$

在给定的时间下，粒子出现在任何位置的概率均由 wave function 决定

分布的平均位置 ->考虑概率分布函数的期望

波函数的基本性质 ->归一化条件

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{\Phi }}^{\ast }(x)\mathrm{\Phi }(x)dx=1$$

波函数正交

$$\int {\mathrm{\Psi }}_n(x){\mathrm{\Psi }}_m^{\ast }(x)={\delta }_{nm}$$

当且仅当 $n=m$ 时, ${\delta }_{nm}=1$ 其余均为 0

de Brogile wavelength: 德布罗意波长公式
wavefunction 中的 $k$ 与栋梁有如下关系

$$\begin{array}{rlr}& p=\frac{h}{\lambda }& k=\frac{2\pi }{\lambda }\end{array}$$

注意德布罗意波长公式与能量的结合

$$E=\frac{p^2}{2m}=\frac{h^2}{2m{\lambda }^2}$$

2. 动量确定的自由粒子

对于动量确定的粒子，我们用平面波来描述其状态

• 波函数方程

$$\begin{array}{rlr}& \mathrm{\Psi }(x,t)=A{e}^{i(kx-\omega t)}=A{e}^{i(px-Et)/\tilde{h}}& k=\frac{p}{\hslash },\omega =\frac{E}{\hslash }\end{array}$$

此时其位置在空间中具有一定的概率，我们无法确定其具体位置

$$\rho (x)=|\mathrm{\Psi }(x){|}^2=|A{|}^2$$

• 能量本征态

$$E_k=\frac{p_k^2}{2m}=\frac{{\hslash }^2{k}^2}{2m}$$

• 多确定动量波函数的线性叠加
  对于由多确定动量的波函数线性叠加形成的波函数，其观测到的动量并不处于本征态，观测到动量的概率由其线性系数（可为复数）决定

[!tip]
如果波函数公式只出现 sin 或者 cos,记得用欧拉公式进行分解 ->转为动量确定的波函数方程的线性和，且以上线性系数可为复数

3. 薛定谔方程与海森堡不确定原理

• 海森堡不确定原理
  海森堡不确定性原理指出：在量子力学中，动量和位置无法同时被精确测量。其数学表达式为：

$$\mathrm{\Delta }x\cdot \mathrm{\Delta }p\ge \frac{\hslash }{2}$$

​

• 时间无关的薛定谔方程

动量算子为:

$$-i\hslash \frac{\partial }{\partial x}$$

当波函数满足能量本征态时，我们有：

$$-\frac{{\hslash }^2}{2m}\frac{d^2\mathrm{\Psi }(x)}{d{x}^2}+U(x)\mathrm{\Psi }(x)=E\mathrm{\Psi }(x)$$

其中，$U(x)$ 是外部势能，而 $-\frac{{\hslash }^2}{2m}\frac{d^2\mathrm{\Psi }(x)}{d{x}^2}$ 是动量运算的平方，除以 $2m$。这类似于经典力学中将能量写为 $\frac{p^2}{2m}+U$。

4. 无限深势阱与有限深势阱

A.无限深势阱

无限深势阱描述了一个粒子被限制在一个一维空间区域内（通常是 0 到 L），这个区域之外的势能是无限大。这意味着粒子绝对不可能存在于这个区域之外。

• 波函数方程

$$ \Psi(x) = $$\{\begin{array}{lll}A\sin (\frac{n\pi x}{L})& \text{如果 }0<x<L0& \text{否则}\end{array}$$

$$

其中 n 为整数，通过归一化有 $A=\sqrt{\frac{2}{L}}$

• 能量本征态

$$ E_n = \frac{\hbar^2 \pi^2 n^2}{2mL^2}

$$

能级之间能量不连续，且间距逐渐增大

[!tip] 注意
无限深势阱对应的电子激发问题一般先考虑基态

B.有限深势阱
有限深势阱与无限深势阱类似，也描述了一个粒子被限制在一个区域内。但是，这个区域之外的势能不是无限大，而是一个有限的值，通常记为 V₀。

• 势能方程

$$\begin{array}{rlr}& U(x)=0,-\frac{L}{2}<x<\frac{L}{2}& U(x)=U_0,x\le -\frac{L}{2}\text{ or }x\ge \frac{L}{2}\end{array}$$

注意此时边界条件为波函数与波函数的导数在边界处必须连续

• 波函数方程

内部通解为:

$$\mathrm{\Psi }(x)=A\sin (kx)+B\cos (kx)$$

外部通解为：

$$\mathrm{\Psi }(x)=C{e}^{ax}+D{e}^{-ax}$$