#PHYS214

Harmonic Waves

基本形式

沿 x 轴正向传播的单一频率的简谐波，形如：

$$ y(x,t) = A\cos(kx- \omega t+\phi) $$

具体而言，沿 x 轴方向偏振的电磁波可以写为：

$$ E_{x}(x,t) = E_{max}\cos(kx-\omega t+\phi) $$

相关参数

71c8206900fc421754c6d97e5563e74.png
基本转化

$$ \begin{align} & k = \frac{2\pi}{\lambda} \text{ 描述波在空间上重复的速率}
& \omega = 2\pi f
& T = \frac{1}{f}
& v = \frac{\omega}{k} = \lambda f (描述波传递的速率，波长除以周期)
\end{align} $$

振幅与光强：
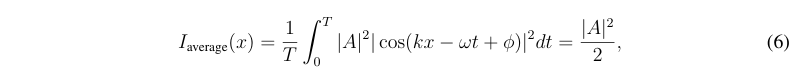
075f37b7a0b23c0015e5edf892b8a2e.png
amplitude at a given position and time: $y(x,t)$

Interference

Superposition of waves

相同波长、振幅、波速的波的叠加

$$ \begin{align} & y_{1}(x,t) = A\cos(kx-\omega t+\phi_{1})
& y_{2}(x,t) = A\cos(kx-\omega t+\phi_{2})
& y_{total}(x,t) = y_{1}(x,t) + y_{2}(x,t) = 2A\cos\left( \frac{\phi_{1}-\phi_{2}}{2} \right)\cos\left( kx-\omega t+\left( \frac{\phi_{1}+\phi_{2}}{2} \right) \right) \end{align} $$

相互干涉的波之间的相位差影响平均强度

不同振幅的波的叠加 ->考虑 Phasors 相量图，通过矢量相加

多个不同振幅，不同相位波的叠加:
考虑将每个向量 $A_{i}\cos(\phi_{i})$ 画在向量图中，然后进行矢量相加（可以利用正交分解）

Example

Two speakers
这个例子展示固定相距距离，且两个声源振幅相同叠加的情况
e67fc63594095c25c3c3317ba73390e.png
cf2aacf382f7ee2839a35fe9af03d27.png

核心还是考虑相位差的来源:
一般为

$$ \frac{2\pi}{\lambda}\Delta r + \Delta \phi_{0} $$

Two slits 双缝干涉实验
c8a3dfb15826994826168a6e37217e0.png
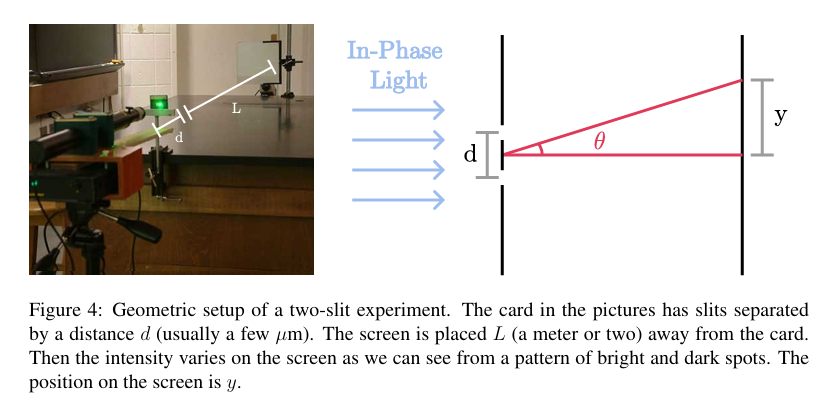
2ba8144630be98320876882bb407d64.png
将两缝分别视为独立的波源（波长相同，相位相同，振幅大小取决于缝的宽度），屏幕上不同的光强由不同点到双缝的距离不同导致）

核心影响因素：光程差

$$ y_{total} = 2A\cos\left( \frac{k\Delta r}{2} \right)\cos\left( \frac{kr_{1}+\phi_{1}+kr_{2}+\phi_{2}}{2} -\omega t\right) $$

光程差近似： $\Delta r=d\sin \theta$
当光程差为波长的整数倍时发生相长干涉；为 $\frac{1}{2}$ 个波长加整数时为相消干涉
d1c770de923cfa76dc85bb7951e0f2d.png

$$ y_{m} =L\tan(\theta_{m}) $$

考虑近似 $\theta=\sin \theta=\tan \theta$,可以得到各个亮纹的位置

$$ y_{m} = m\frac{L\lambda}{d} $$

Interferometer 干涉仪

182b3d447a1e01e6a985d4a35560c71.png
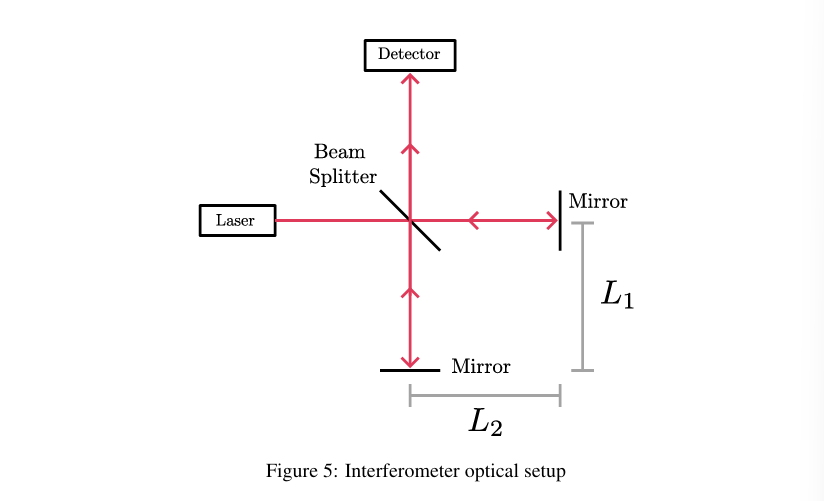
882d0dfc9cac8acab635c080bbdd015.png
核心因素: 两路径上的光程差,注意为到反射镜距离差的两倍

$$ \Delta r = 2(L_{1}-L_{2}) $$

$$ \Delta \phi= \frac{2\pi}{\lambda}\Delta r = \frac{4\pi}{\lambda}(L_{2}-L_{1}) $$

Diffraction 衍射

Diffraction from a single slit

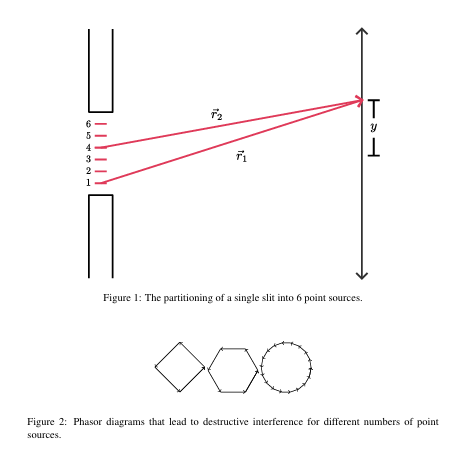
9e5120f8f2df20dd37664ed6fb0d2d7.png
先考虑使光强为 0 的角度 $\theta_{0}$ ，确定光斑大小

$$ k(r_{2}-r_{1}) = \frac{2\pi}{N} $$

其中 $r_{2}-r_{1}=\frac{a}{N}\sin \theta_{0}$,推出

$$ a\sin \theta_{0} = \lambda $$

则

$$ y_{0} = L\tan \theta_{0} $$

Diffraction for a circular aperture

推导过程与单缝类似，对于直径为 $D$ 的圆孔，需满足的条件为

$$ D\sin \theta_{0} = 1.22\lambda $$

Diffraction from multiple slits

c9f5e7b3b252bfef7cae96966c2be8e.png

Example: Diffraction and lithography

Lithography Machine 光刻机
05dcc5c7e4110269456279e44d8d4f2.png
一般情况下我们希望衍射光斑尽可能小 ->希望 $\theta_{0}$ 尽可能小,以区分不同的对象
当波长增加时，蚀刻的孔径增大
当透镜直径增大时，蚀刻的孔径减小

计算思路

Example: Homework3.4