#Math241

Vector-valued function

Basic

Definition

vector-valued function, or vector function, is simply a function whose
domain is a set of real numbers and whose range is a set of vectors
即将 $\mathbb{R}\to \mathbb{R}^{n}$

Parametric Curve & Non-Parametric Curve

Parametric Cruve

参数化曲线：将曲线的每一维都表示为关于某个参数 $t$ 的函数

将非参数的曲线转化为参数化的曲线
Example:

注意：一个非参数的曲线可以有多种参数化的表示
Closed Parametric Curve:

Limits and Continuity

Basic Term

Notation

• $B_{r}(a)$ 表示以 a 为球心，r 为半径的球，不包括边界
• $S_{r}(a)$ 表示以 a 为球心，r 为半径的球壳
  
  

Topology

• interior point：内点，即考虑以 a 为中心的小球仍包含在一个子域 D 中， 记 D 为 a 的邻域
• boundary point: 边界点，即以 a 的为中心的任意球一定包括子域 D 内与域外的点
• limit point: 三维域内存在序列极限趋于 a(注意 D 内的点一定是极限点，同时包含其边界)
• accumulation point: 即 a 点周围稠密（任意取一个小球都能包含 D 中其他一个点）

注意紧集的定义 ->closed and bounded

Concept

• 无穷点序列的极限 Limit of a Sequence
  即序列中的所有点收敛到空间中一个点（利用球的半径去刻画极限），或者即对向量的任何一个分量都在该点出有极限

一旦确定收敛，极限便唯一确定

• 曲线的极限与连续性 Limits and Continuity for Curves
  
  极限存在：即为可以通过控制自变量与特定点的距离，进而控制映射出的 n 维向量在对应极限的任意小的 n 维球内

极限：外层向量函数的极限等于各内层维数上函数分别趋近

$$ \lim_{ t \to a } r(t)= <\lim_{ t \to a } f(t),\lim_{ t \to a } g(t),\lim_{ t \to a }h(t)> $$

连续性: 即对任意一个内层函数都在 a 处收敛

$$ \lim_{ t \to a } r(t) = r(a) $$

• 考虑在现实中的泛化定义（考虑非标准化的基与原点的平移）
  

证明直接考虑用矩阵表示线性变换，然后即可将原空间中的基转化为标准基，然后直接将对应的极限加和即可

Differentiation and Integration

Differentiation

Concept

• 定义
  与之前极限的定义类似，只要每个分量上对应的函数可导即可；对于换底 + 平移后的空间同样适用
  
• 切线
  即切点加对应导数确定方向构成的直线
  

Differentiation Rules

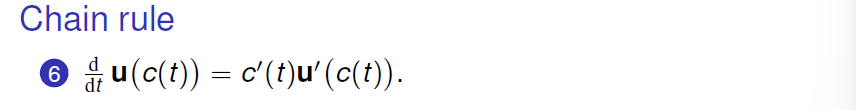
Proof:

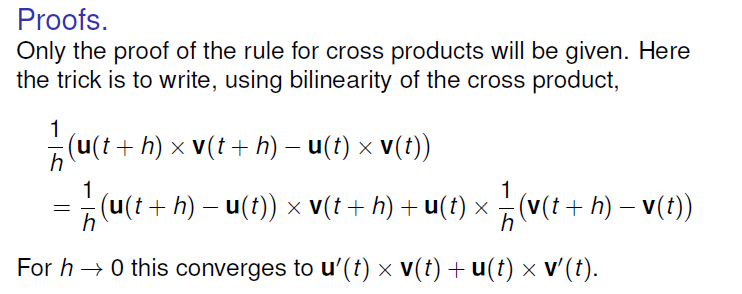
当曲线的模长为定值时, $r’(t)$ 总与 $r(t)$ 正交

注意对曲线模的求导：

$$ |r(t)|’|r(t)|=r(t)\cdot r’(t) $$

Integration

Arc Length

Definition

关注 Slides 上关于 Arc Length 基于任意划分区间计算得到的最小上界/对划分区间取极限所得到的两种定义

计算曲线长度的公式

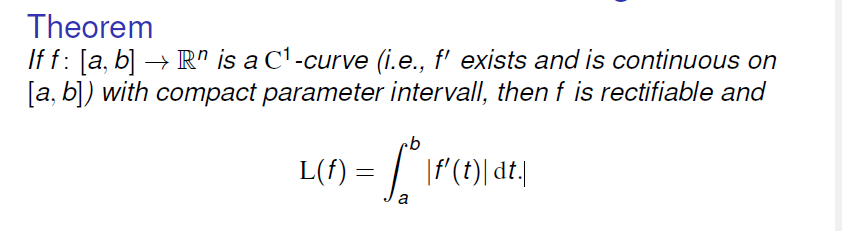
只要曲线为 $C^{1}-curve$（在闭集上可导且连续） ,即可直接从导数的模长积分得到最终的曲线长度

Piece-wise $C^{1}-Curves$: 即将每一段可以直接用的 $C^{1}-Curve$ 直接积起来即可

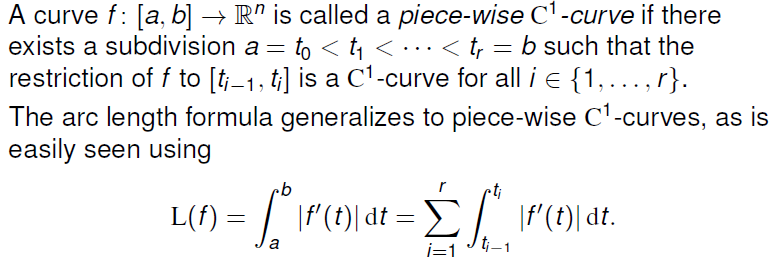
注意，对于这样的曲线需要满足在整个区间上连续，并且在断点处两边的单侧极限相等

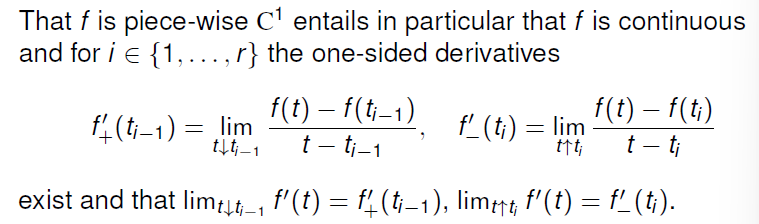
Arc Length Function

注意：以曲线长度对曲线进行参数化：

• 可以先考虑积分表示曲线长度函数，然后根据结果合理换元
• 见 Worksheet4

Uniform Continuity 一致连续

Definition

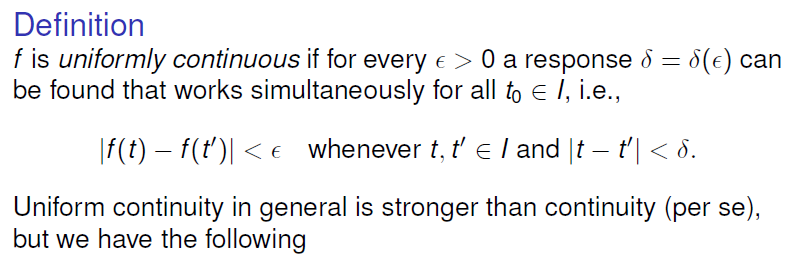
核心即为确定对于曲线上任意的点，我们可以找一个不取决于具体点的最小 $\Delta$ ,即可控制任意逼近

连续 + 紧集 ->一致连续

Parametrization with Respect to Arc Length

核心即为对 Arc Length 积分后通过换元，使得基本的元表示单位曲线的长度
->基于此，我们容易得到其导数为单位向量（结合反函数的性质以及曲线长度函数的定义即可）

Curvature 曲率

**Smooth Curve 定义：在定义域上 $r’(t)$ 存在且不为零

对于一个由 $r(t)$ 定义的光滑的曲线，单位切线向量即为：

$$ T(t) = \frac{r’(t)}{|r’(t)|} $$

利用切线单位向量与单位曲线长度的比值的模长来衡量曲线方向变化的速率 ->即为曲率

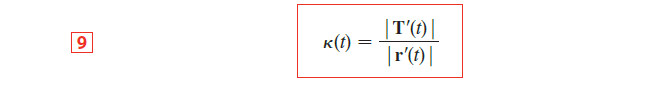
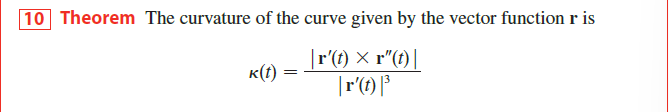
对于特殊的由 $y=f(x)$ 表示的曲线，我们有

Normal and Binormal Vectors

Vectors

• 定义 $T(t)$ 的单位法向量
  由 $T(t)$ 的模长恒为定值，我们容易得到 $T’(t)$ 与其正交
  1. 再由两者叉乘得到第三个法向量 $B(t)$
  2. 注意为避免计算的复杂性, $N(t)$ 与 $T(t)$ 可直接利用对 $r(t)$ 求一二阶导得到其对应的方向
     

还可以利用正交化的方法分别计算 T(t) 与 N(t),即考虑正交化 $f’(t)$ 与 $f’‘(t)$

利用取二阶导并减去其在一阶导上的投影得到，避免复杂计算与求导

Planes

• Taylor’s Formula for Curves

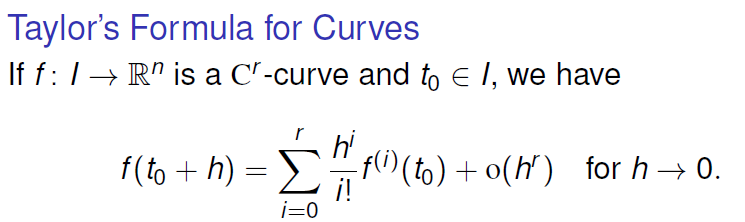
• Big-O and Little-o Notation
  大 O 表示两者关系为常数，小 o 表示可以在此量级上任意小
  

• Normal Plane
  由 Normal Vector 与 Binormal Vector 决定的平面,法向量即为单位切线向量
• Osculating Plane 摆动平面
  由 T 与 N 确定的平面，法向量为 Binormal Vector

• Center of Curvature and Osculating Circles
  经过曲线上一点，半径为 $\frac{1}{\kappa}$,距点 P 方向即为 N
• Evolute: the movement of the center of the osculating circle

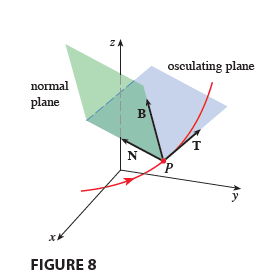
$$ e(t) = f(t) + \frac{1}{\kappa(t)}N(t) $$

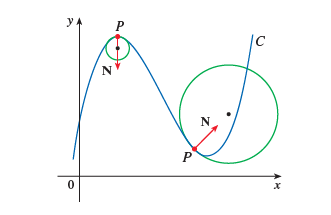
当空间曲线本身位于一个平面内时，其摆动平面即为其所位于的平面

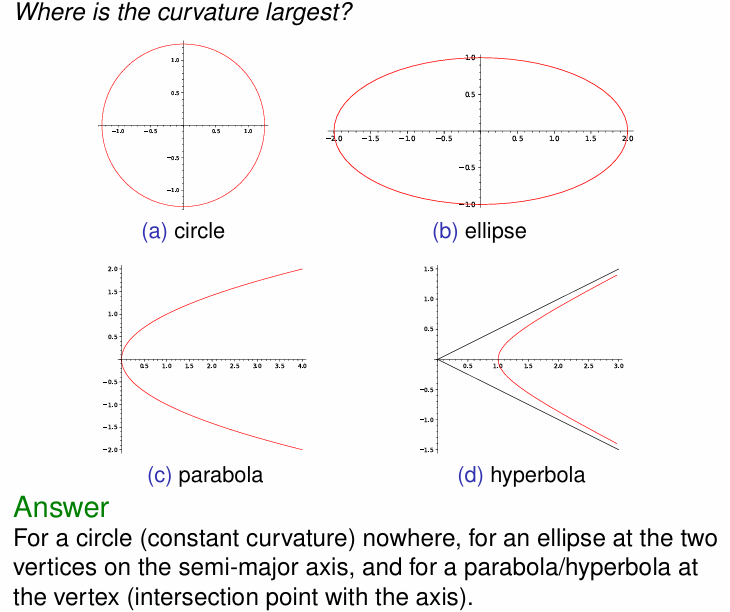
注意：可以用曲率最值判断何为空间中曲线的顶点
Example:
Find the vertex of parabola $(1+t,1+t^{2},t+t^{2})$ in $\mathbb{R}^{3}$

总结

Torsion

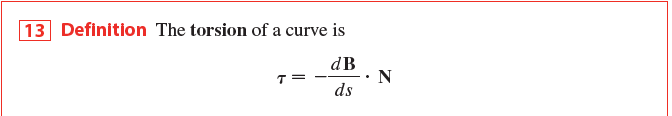
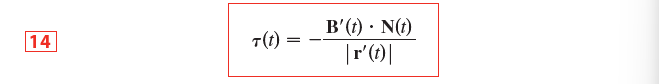
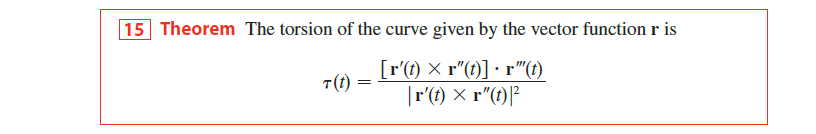
当以曲线的弧长参数化时，我们有