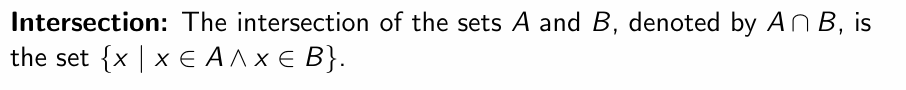#Math213

Sets

Basic

• Concept: A set is an unordered collection of objects. The objects are called elements or members.(强调无序性)
• Representation:
  
• Subset:
  
• Size-Carinality 集合的势
  
• Power Set: 集合所有子集的集合

Tuple and Cartesian Product

• Tuple:Tuple 强调元素的有序性
  

• Cartesian Product: 各集合元素的有序组合
  
• Relation: **A subset of of the Cartesian product $A \times B$ is called a relation from the set A to the set B

Operation

• Union:
  
• Intersection
  
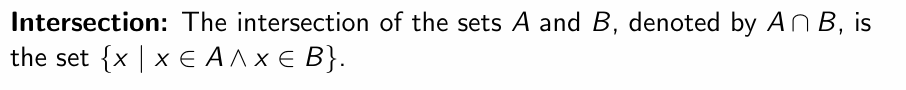
• Difference
  
• Complement
  

Identities

Function

Basic

• Concept
  
  domain: 定义域
  codomain: 上域
  range：值域
  $f(a)=b$: a 为 preimage, b 为 image
• Type
  1. injective: 单射函数，不同的像对应不同的原像
     one-to-one
     
  2. Surjective: 满射函数，对任意的像都有原像与之对应
     即陪域中每个元素都被覆盖
     onto
     
  3. Bijective: 双射函数，既为单射又为满射
     one-to-one correspondence
     
     证明 Bijective Function: 证明单射和满射即可

1. Inverse Function
   

Composition of Functions

Concept

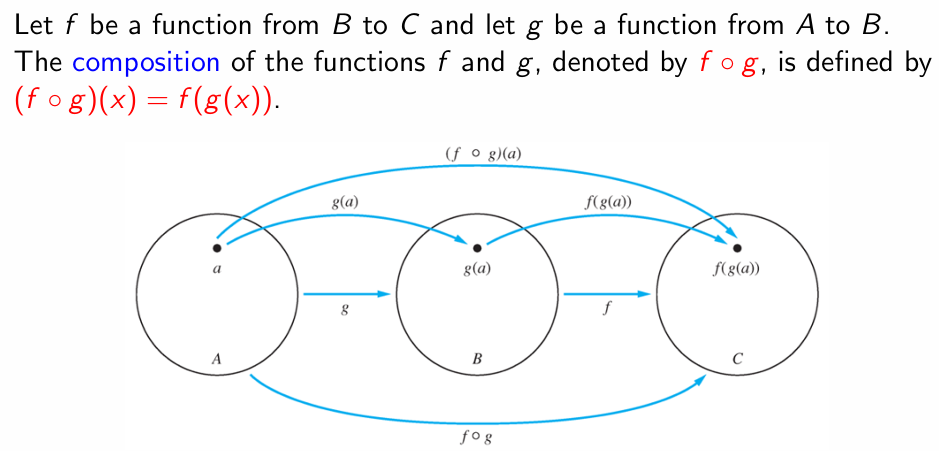
对于双射，映射及其逆映射的复合即为 Identity Function

Special Function

• Floor and Ceiling Function
• Factorial Function

Sequence

Definition

还可利用递归形式定义

确定初始项，然后即可根据后项与前项之间的关系定义

Common Types

• Geometric Progression: 等比
• Arithmetic Progression: 等差

Cardinality

Countable

The elements of the set can be enumerated and listed

考察集合的势与正整数集势的关系

Core: check one-to-one correspondence 或者寻找一种合理的排列方式

Notice: 正有理数集可数，考虑控制分子分母的和，然后逐项列举

注意有理数集，代数集可数

Uncountable Set

$\mathbb{R}$ , $(0,1)$ 不可数，康托尔对角线

证明集合的势相等：考虑构造两者相互的 one-to-one correspondence

Computable

P: 表示 Power set,即集合所有子集构成的集合