#Math241

Differentiable Maps

Intuition of Differentiation

进行微分的核心目的即为利用线性映射对局部进行拟合估计
-> 追溯微分的定义式，我们可以考虑将函数在某点处附近增量表示为 原值 +Linear h+ Remainder 的形式

• Remainder 余项可用 small-o notation 表示，核心即为需要满足：

$$ \lim_{ h \to 0 } \frac{R(h)}{h} = 0 $$

Example

对于不能简单用多项式函数表示的情况 ->考虑直接展开成多项式形式

Concept

Notes

• 可以用极限替代小 o 记号

• 线性映射是唯一的
  

• Jacobian Matrix->表示 h 不同维线性组合的系数
  

• Coordinate-wise Differentiation

More on Examples

• Linear and Affine Maps
  

• Quadratic Forms

• Length Function

Partial Derivatives

Definition

偏导：考虑固定其余变量，考察函数关于某一特定变量的变化率

注意

• 偏导函数的定义域 ->相对应的点对应的微分极限存在
• Differentiability -> Partial Differentiability

Theorem

• 注意雅可比矩阵的写法：每一行即为一个映射，每一列依次为对不同的变量求偏导
• 靠近 x 偏导存在且偏导函数连续 ->f 在 x 处可导

Example

注意偏导在存在 (0，0) 存在取值，但是极限不存在 ->不连续

Further Concept

Directional Derivatives

Definition: 即从一个方向趋近函数求其微分
注意方向微分的基本定义，可以从基本定义出发判断该方向微分是否存在
例如 Worksheet 7

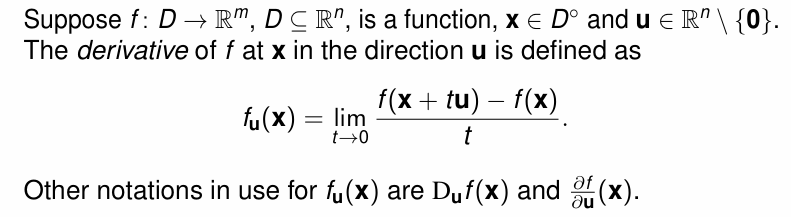
Notes:

• Functional Vector 的模常常会影响 Functional Derivatives,所以我们一般选取单位向量
• 当 m=1（即映射结果只有 1 维时），如果选取的方向向量方向与 $J_{f}(x)$ 相同或相反，我们可以得到 $G_{f}$ 的最大值或最小值
  

注意对于 Directional Derivative,我们有 $f_{u}(x)=df(x)(u)$
或：

$$ D_{u}f= \nabla f \cdot u $$

利用单位方向向量与梯度的点乘确定 Graph 在某个方向上的斜率

当方向向量与 Gradient Vector 同向时，其微分有最值（利用点乘关注两向量的夹角）

Jacobi Matrix矩阵的每一列表示了相对应变量在微分上的方向向量

Gradient

Definition

gradient 即为函数关于所有 x 分量偏导的列向量,雅可比矩阵行向量的转置

Properties:

• gradient 向量的方向即为函数值变化最快的方向,可以从 directional derivative 与 coutour map 角度考虑
• gradient 向量的方向与 f 的等高线图垂直（注意可以利用 gradient 方向判断 contour 的切线方向） 直接考虑对 contour 两侧同时求偏导即可得到 Gradient 与 Contour 对应点的 Tangent Vector 正交

注意 gradient vector 与 directional vector 的结合

Tangent Space

核心即为利用微分实现对于函数的局部线性近似

Tangent Space 即为多元函数对应的自变量及其线性近似函数值向量拼接成的结果构成的线性空间
或者理解为对函数 f 的 Graph $G_{f}$ 在给定点 $(x_{0},y_{0})$ 附近的线性近似空间或者切空间，表示为函数 A 的 Graph

函数 A 即为对应的线性近似函数：

$$ A: \mathbb{R}^{n} \to \mathbb{R}^{m}. x\to f(x_{0})+L(x-x_{0}) $$

• 可以用参数形式表示，写为对应点 + 线性近似的向量
• 可以直接用方程形式表示（及类似与切线，仅需要将之前的斜率换成微分对应线性映射 A
• 关注 m=1 的特殊情况
  

在三维空间中的直观定义：

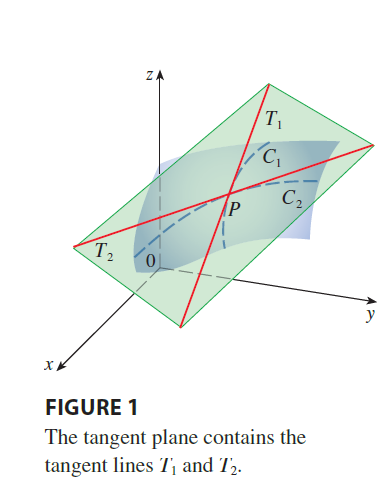
重点关注三维空间中的公式

通过引入参数化曲面定义 Tangent Space

Smooth 定义: 当参数曲面对应的映射可微，且雅可比矩阵列满秩时，参数曲面光滑

进一步地，我们定义 Tangent Space

Tangent Space 即为利用微分对多维函数在局部进行线性近似，此时 T 为 $\mathbb{R}^{n}$ 中一个 k 维仿射子空间（在雅可比矩阵列满秩时）

$g(x_{0})$ 即为多维函数的局部待近似点（或者为仿射空间的偏移向量）， $J_{g}(x_{0})h$ 即为对应的线性近似空间

The Meaning of Differentials

• dx即为恒等映射函数的微分
• **$dx_{j}$ 即为函数 $\mathbb{R}^{n}\to \mathbb{R},x\to x_{j}$ 的微分
• $dz$ 一样考虑对于复数的恒等映射

The Multivariable Chain Rule

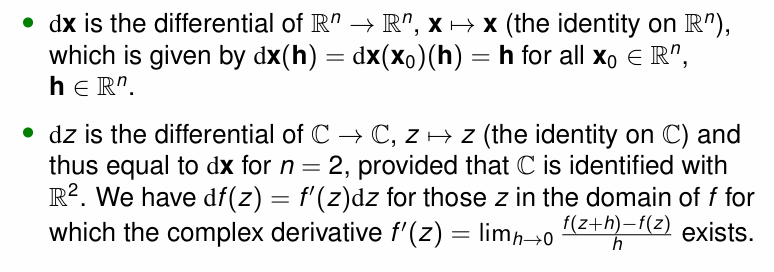
Theorem:

证明：
核心即为利用每一步可微带来的线性表示形成最终的复合表示，在证明过程中需要验证的即为是否满足线性


验证后面均为关于 h 的小项

推论 1（考虑 Matirx Form 形式的 Chain Rule)

用矩阵形式表示微分的线性算子

Remark:
即对于一个多元函数经过多步映射得到的最终结果，如果我们需要考察最终结果关于初始变量的偏导，则需考虑整个复合映射过程所涉及到的所有中间变量，通过 Chain Rule 逐级向前得到最终结果

推论 2 (考虑梯度与 contour 切线向量的垂直关系)

注意：

• Smooth Parametrization 即意味可以找到参数对 f 中的 x 进行参数化，且同时新实现的映射可微
• 进行参数化是为构造一个曲线，使得可以关注曲线上的切线以及对应映射后结果梯度的关系
• 对于映射到 n 维的情况，当我们考虑 n 维变量的 Level Surface 时（相当于对其加上一个限制条件）,在对应的 f 为 $C^{1}$ function(偏导存在且在定义域上连续) 且其 gradient 不为 0，我们即可找到对应 $n-1$ 维的参数化曲面，在此情况下函数 f 在点 $x_{0}$ 的梯度正交于参数化曲线 $S$ 在该点的切空间
  $g:\mathbb{R}^{n-1}\to \mathbb{R}^{n}$
  

考虑更具体的情况，如果需要求解对应参数化曲面的 Tangent Plane，只需要考虑：

$$ \nabla f(x_{0}) \cdot(x-x_{0}) = 0 $$

或者利用之前对于对应参数化曲面 Tangent Plane 的求法：

$$ \text{Tangent Plane: } x_{0} + \mathbb{R}\text{ Columns of Jacobi matrix of g} $$

Example

推论 3 Inverse Function Theorem

前置条件: $C^{1}$ Curve + 对应的雅可比矩阵列满秩
结论：可以在限制的定义域范围内找到函数 $f$ 的逆 $C^{1}$ curve