#Math213

Mathematical Induction

注意：

• 归纳奠基（选择最小满足命题的正整数）
• 假设，并利用前向假设证明后项命题

Recursion

Towers of Hanoi Problem 汉诺塔

• Description
  

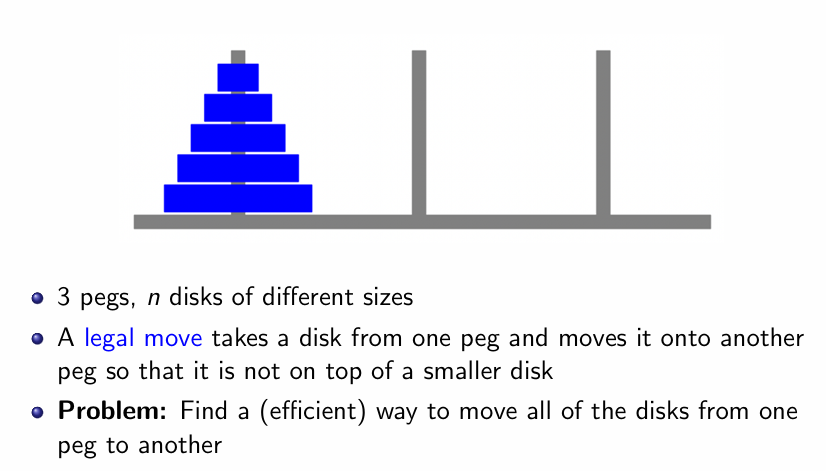
• Algorithm
  
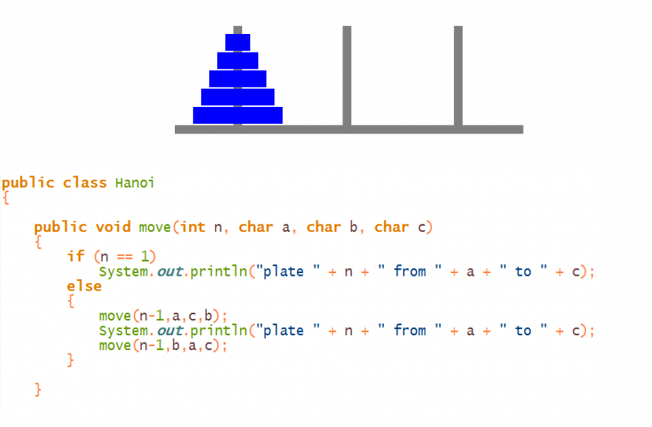
  注意汉诺塔核心即为考虑到最后的情况必有 n-1 plate 在第二块，1 一个最大的 plate 在第一堆，这样即可将问题化归为 n-1 的情况，调用递归函数

• Idea
  递归的数学核心可视为反向数学归纳法，当我们确定了递归最终可以结束（即确定归纳法的奠基），再寻找到将问题递归的方式，即可形成完整的递归链条
  
• Running Time: 利用操作次数表示

$$ \begin{align} & M(n)\text{ denotes the number of disk moves needed for n disks}
& M(1) = 1
& M(n+1) = 2M(n)+1 \

\end{align} $$

Recurrence

• 递归函数或方程定义
  
• 核心
  Basic Step（初始情况）
  Recursive Step（递归过程）

Linear Recurrences

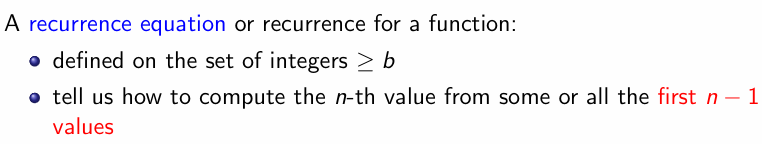
相关概念

• 线性递归：

$$ a_{n} = f(a_{n-1},\dots ,a_{n-k}) = s_{1}a_{n-1}+\dots+s_{k}a_{n-k}+f(n) \text{ 其中对应的s与f(n)均为实数} $$

• 线性齐次递归 (Linear Homogeneous Relation)：
  在线性递归的基础上要求递归表达式中无多余的常数，即 $f(n)=0$
  注意系数本身不一定要求为常数，可为与 n 有关的函数
• 线性递归的阶数或度数 (order/degree)
  当前项与最远项之间的差距

1. 一阶线性递归
   • 定义

$$ T(n) = f(n)T(n-1)+g(n) $$

First Order: 递归表达式只出现前一阶情况
Linear: 出现的递归式均为一次

Theorem

$$ \sum_{i=1}^{n}ix_{i}^{i} = \frac{nx^{n+2}-(n+1)x^{n+1}+x}{(1-x)^{2}} $$

1. 齐次线性递归特征根方程

n 阶齐次线性递推数列系数为常数（简称线性递推数列）是指形如：

$$ a_{n}=c_{1}a_{n-1}+c_{2}a_{n-2}+⋯+c_{n-1}a_{n}+c_{n}a_{0} ​ $$

的数列，其中 $c_{1},c_{2},\dots,c_{n}$ ​为常数系数，且是齐次的，即右边没有常数项。
特征根方程的求解

• 将递推数列的系数代入特征方程，得到一个关于 r 的多项式。
• 求解该多项式，得到所有的特征根 $r_{1},\dots ,r_{n}$
• 结合 n 个初始项得到最终表示（如果初始项不足可能会有非唯一解）
  特征根的情况及其对应解法
• 不同的特征根（无重根）：若特征方程有 n 个不同的根 $r_{1},\dots,r_{n}$ ​，则通解为：

$$ a_{n} = A_{1}r_{1}^{n} + A_{2}r_{2}^{n}+\dots A_{n}r_{n}^{n} $$

• 有重根的情况：若特征方程有某个重根 r，重根的情况需要考虑不同阶数的 $r^{n}$ 乘以多项式。若重根 r 的重数为 k，则通解的一部分是：

$$ (A_{1}+A_{2}n+\dots A_{k}n^{k-1})r^{n} $$

• 复根情况：直接用实根相同方法解决，或考虑其指数与三角形式利用 DeMoivre’s Theorem 化简
  

1. 线性非齐次递归
   形如:

$$ a_{n} = \sum_{i=1}^{k}c_{i}a_{n-i} + F(n) $$

线性非齐次递归解的形式形如特解与其对应的线性齐次递归的通解之和

如何寻找特解 ->无一般通解形式，但可对特殊情况进行分类讨论

• 多项式
• 指数函数
  利用待定系数法求解，同时关注特征方程根与非齐次函数指数的底数相同的特殊情况
  

对于特殊情况，注意再待定系数前乘上对应根的重数次幂 n

[!warning] 注意

• 数列递推的求解一定要注意初始情况与特殊情况，关注是否递推表达式对所有 n 都满足
• 线性齐次递归的系数不一定要求为常数
• 注意对于非齐次线性递归发现其特征根为 1 时，在求解特解的过程中需意识到特解多项式也乘了 1 对应的指数幂，所以要根据重数相应升次

Growth Rate of Solutions to Recurrences

Divide and conquer algorithms

Problem Form

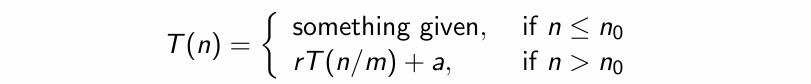
Binary Search

Growth Rate Type

Theorem

$$ T(n) = a^{\log_{2}n}T(1)+n\sum_{i=0}^{\log_{2}n-1}\left( \frac{a}{2} \right)^{i} $$

$$ n\sum_{i=0}^{\log_{2}n-1}\left( \frac{a}{2} \right)^{i} = \frac{n\left( 1-\left( \frac{a}{2} \right)^{\log_{2}n} \right)}{1-\frac{a}{2}} $$