
#Math241
1. Definition

特征函数

2. 利用特征函数对于重积分定义域的自然延拓

基于特征函数,现在我们可以把重积分原有函数在整个空间中局部区域的积分转化为在整个空间上的积分,减少复杂性


1. Definition
[!tip] Summary
- 基于区间长度定义 n 维区间的体积
- 定义 Step Function(一定数量定义在 n 维区间上特征函数的线性和)
- 定义 Step Function 的积分 ->自然考虑对应数量 n 维区间体积的线性和

2. Theorem
[!tip] Theorem
- 任意一个 Step Function 均可以表示为定义在若干个 n 维不交的区间上的特征函数的线性和
- 如果 Step Function 存在多种表示形式,其积分的结果相同


L1 半范数用于对恒大于等于 0 的函数 f 的横截面定义外测度
1. 实数集上的算数扩展(考虑无穷的代数运算)

2. Enveloping Series 包络级数

核心想法即为使用多个 n 维区间上的特征函数对函数 f(x) 实现覆盖,利用多个特征函数的线性和近似 f,并且通过取和估计 f 的覆盖范围
3. L1 半范数

函数 f 的 L1 半范数是其包络级数的下确界
4. Cauchy Sequence->用于描述数列的收敛情况

柯西数列均收敛
扩展到级数的情况 ->考虑利用绝对值收敛证明级数收敛

5. Lebsegue Integral
勒贝格积分的核心即在于可以对函数 f 找到一个收敛的包络级数,最终使得函数的积分可以定义为包络级数的积分

Remarks

1. 证明狄利克雷函数勒贝格可积


证明核心:通过在离散的有理数附近取可以任意小的开区间建立狄利克雷函数的包络级数,同时我们可以该包络级数的积分任意小

[!warning] 注意
f 可积可以推出 f 可积,但是 f 可积不一定能够推出 f 可积 - 考虑两个函数乘积是否勒贝格可积时注意除了满足 f1,f2 本身可积,还需要满足有界

当函数在 $\mathbb{R}$ 上的每一个有界闭区间 (紧集) 上黎曼可积时,当且仅当其 improper 黎曼积分收敛时,函数 f 在 $\mathbb{R}$ 上勒贝格可积(核心为关注其 improper 黎曼积分的收敛性)

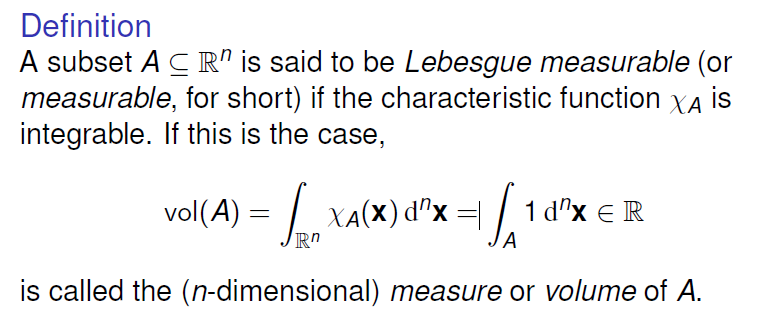

[!tip] Summary
- 一系列可测集的交集仍为可测集
- 当一系列可测集其测度之和小于无穷时,他们的并集可测。特别地,当这些可测集两两不交时,其并集的测度等于这些可测集的测度之和 (核心性质: $\sigma$ 可加性,注意满足无穷可加性)
- $\mathbb{R}^{n}$ 中有界闭集可测
- $\mathbb{R}^{n}$ 中有界开集可测
- 存在有界集不可测
- $\mathbb{R}^{n}$ 中所有可数集测度均为 0(可数集可以被枚举,我们可以在其枚举出的每一个元素周围定义足够小的区间)
- 测度为 0 的集合子集仍为可测集
- 每一个 $\mathbb{R}^{n}$ 有界开集均可以用可数个有界闭集覆盖

Definition

Theorem: 测度为 0 的集合的等价表述

Example:$\mathbb{R}^{n}$ 中的光滑超曲面测度为 0

直观解释:
光滑超曲面 $S$ 是一个 $n-1$ 维的集合,在 $n$ 维的空间中没有足够的“厚度”来贡献非零的体积。可以将其类比为平面在三维空间中占据“零体积”,或者曲线在二维平面中占据“零面积”。
性质几乎处处成立的定义 ->利用其否命题测度为 0 描述

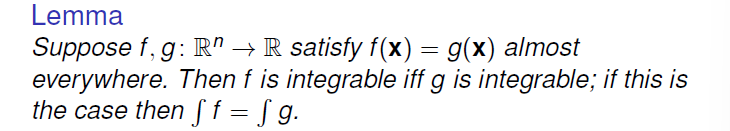
单调有界定理

[!tip] 单调有界定理
给定一个定义在 $\mathbb{R}^{n}$ 上不减的可积函数序列,且序列中函数的积分有界。那么我们可以定义这个序列的极限函数 $f(x)=\lim_{ k \to \infty }f_{k}(x)$ ,同时我们可以交换这个序列上函数的积分与该极限函数的积分 $\int f=\lim_{ k \to \infty }\int f_{k}$单调有界定理描述了在特定条件下,如何将一列函数的积分极限与其点极限交换顺序
Notes: 核心为可积函数序列不减,且有独立于 k 的上界
- 该极限函数也被称为函数序列 $f_{k}$ 的 point-wise limit,因为对于每一个参数 x,我们可以单独验证其收敛性
- 对于一个不减的函数序列,我们有其积分序列不减,那么其要么有界,要么趋于无穷
- 可积函数必须处处有限

Example

考虑一个嵌套的可测集序列,记其嵌套集合的并集为 A,f 在 A 上可积当且仅当 f 在该嵌套集合列中每一个集合上均可积,且其绝对值积分有界。此时我们可以通过其嵌套序列的极限积分去计算 f 在 A 上的积分
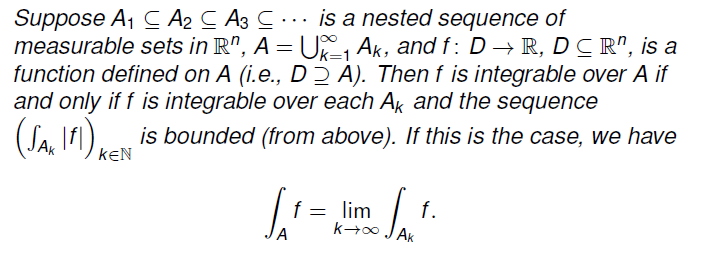
先确定寻找到的可测集序列满足嵌套关系,再确认其于每个集合上可积,且其绝对值积分可以找到不取决于 k 的上界
Example1


Example2: Gamma Function




[!tip] 有界收敛定理
若 $\mathbb{R}^{n}$ 上可积函数的序列处处收敛,且存在一个独立于 k 的可积函数 $\Phi\geq 0$ 满足对该序列中任意的函数均有 $|f_{k}(x)|\leq \Phi(x)$. 那么这个序列的极限函数可积,且有 $\int f=\lim_{ k \to \infty }\int f_{k}$
Notes
- 又名支配收敛定理, $\Phi$ 为支配函数
- 相比于单调有界定理,不要求严格的函数序关系,但是要求存在极限函数
引入参数,利用在对参数 y 范围内积分的基础上定义关于 x 的函数

注意需要满足 f 可积
[!question] 如何利用 f 的性质研究函数 F 的连续性、可微性以及偏导?

[!tip] Theorem
- 关于 x 定义在 y 的积分上的函数 F($F(x)=\int_{Y}f(x,y)d^{n}y$ 连续条件:
- $x\to f(x,y)$ 对任意的 y 连续
存在可积函数 $\phi$ 可以控制 $ f(x,y) $ 的上界 - F 偏导的性质(即可将微分号移至积分内部): $\frac{\partial F}{\partial x_{j}}(x)=\int_{Y} \frac{\partial f}{\partial x_{j}}(x,y)d^{n}y$ 满足所需的条件
- $x\to f(x,y)$ 对于任意的 x 一阶可微
存在可积函数 $\phi$ 可以控制 $ \frac{\partial f}{\partial x_{j}}(x,y) $ 的上界 (由于可微与连续均为局部的性质,所以该要求可以弱化为对于每一个给定 x 在其邻域内可以找到函数 $\phi$ 控制上界)

Notes


Example

[!danger] 重要技巧
费曼积分法的核心即为为积分式引入新的参数,通过考察其引入新的参数后微分的情况,再得到最终的积分式
Example1






Example2: Dirchlet’s Discontinuous Integral 狄利克雷积分
可以作为勒贝格可积函数的反例


通过不断利用 Fubini 定理,将 n 维重积分不断降维,其中对不同维数积分顺序的选取是任意的

为了应用 Fubini 定理,需要满足 f 的可积性 ->相比于之前的证明,我们考虑用圆面约束

Example2->求解 n 维球的体积


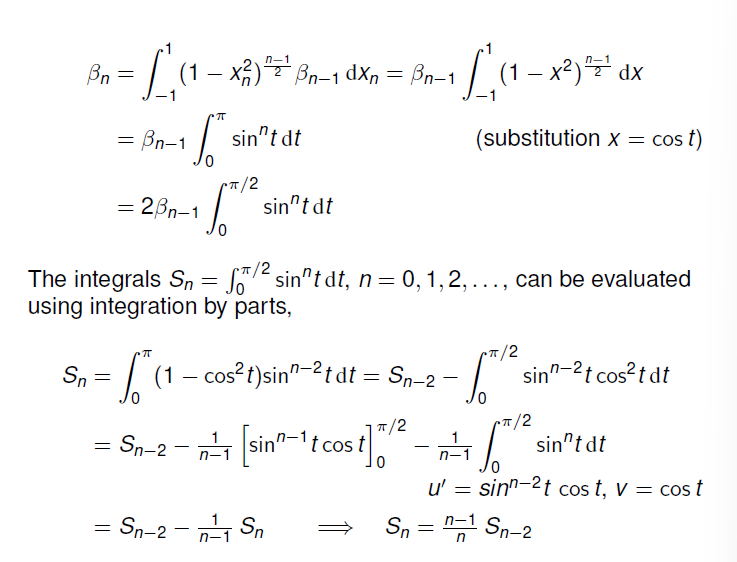

当 n=5 时,n 维球的体积有最大值
[!tip] 局部可积函数
函数 $f$ 局部可积 ->对于任意的 $x \in\mathbb{R}^{n}$, 均存在一个对应的邻域使 $f$ 在邻域上可积。
- 以下这些性质均等价:
- f 局部可积
- f 在 $\mathbb{R}^{n}$ 的每一个有界开集上可积
- f 在 $\mathbb{R}^{n}$ 的每一个有界闭集(紧集)上可积
- f 在以原点为球心,任意有限半径的球内均可积
- 与 Globally Integrable 的比较
- Globally Integrable 要求函数在整个定义域上积分均为有限
- Locally Integrable 仅要求函数在定义域的任意有限区域内可积,函数可能在定义域的某些部分可能区域无穷,但是这些无穷大的区域测度为 0
- 联系与转化
$f$ 局部可积且在范数有限 等价于 $f$ 全局可积- 任意连续函数 $f:\mathbb{R}^{n}\to \mathbb{R}$ 以及通过在测度为 0 的区域函数值为无穷的连续函数 $g:\mathbb{R}^{n}\to \bar{R}$ 均为局部可积


Tonelli Theorem

相比于 Fubini 定理,Tonelli 定理不要求函数绝对勒贝格可积,只要求函数为非负可测函数
为单元微积分中的换元积分在多元微积分中的泛化
单元微积分中的换元积分

换元积分可以扩展到各种形式的区间:
[!tip] 微分同胚概念(Diffeomorphism)
考虑由 $U\to V$ 的映射 $T$ ,其中 $U,V \subset \mathbb{R}^{n}$ ,T 满足
- T 为双射
- T 与其逆映射 $T^{-1}$ 均为连续可微的映射 ( $C^{1}$-maps)( $T^{-1}$ 可微的条件可改写为 $J_{T}(x)$ 满秩

[!tip] 换元理论
对于开集 $U,V \subset \mathbb{R}^{n}$, 且映射 $T:U\to V$ 微分同胚,则有如下换元积分成立。$$ \int_{U}f(T(x))|\det J_{T}(x)|d^{n}x=\int_{V}f(y)d^{n}y $$
- 勒贝格测度与勒贝格积分在欧几里得变换下保持不变( $T(x)=Tx+b$,其中 $T$ 为正交矩阵, $b$ 为平移向量)
- 可以直接用换元积分进行体积的测度转换。特别低,对于线性变换,其体积的变化直接体现在线性变换矩阵的行列式上

Notes
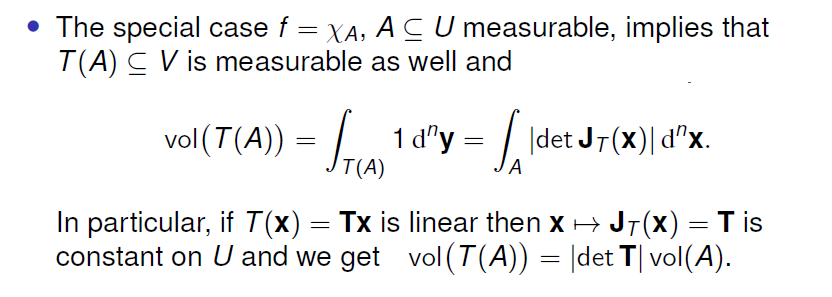

其中极坐标,球坐标,柱坐标在之前均有涉及
[[ Multi-variables Integral#Application & Example ]]


Example:Gauss Integral


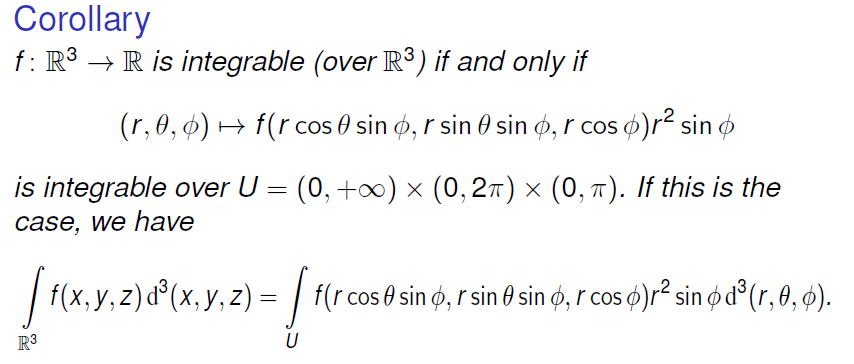
函数值仅由其到原点的距离即 (length function 的取值) 确定

由对应极坐标换元以及球坐标换元的结果即可积出相应的系数
泛化情况
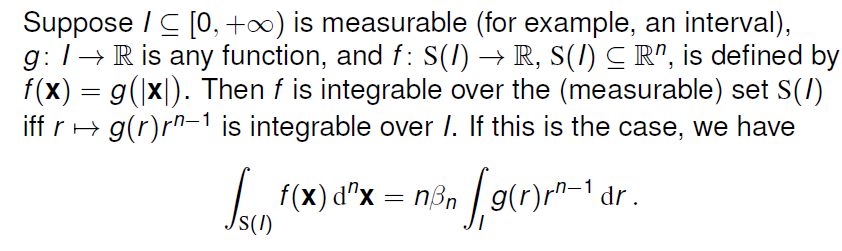
Example1

Example2
