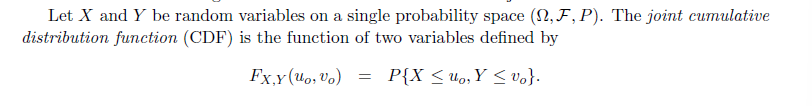
利用图像定义,我们有:
对于分布在一个区域内的联合概率分布,我们有:

Proposition
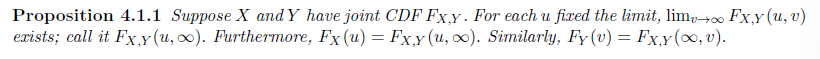
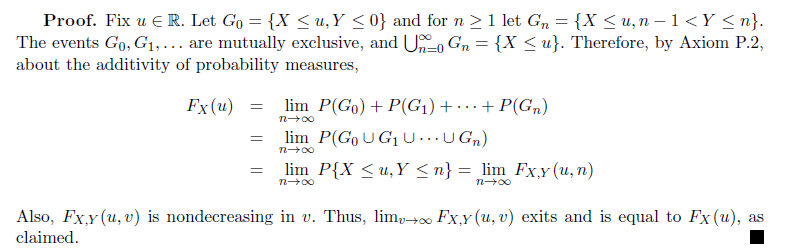
Properties

#ECE313
Definition
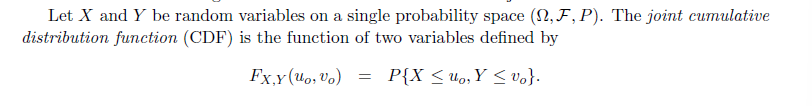
利用图像定义,我们有:

对于分布在一个区域内的联合概率分布,我们有:

Proposition
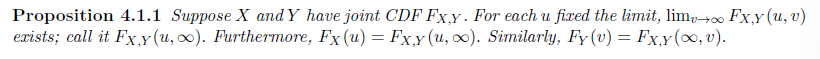
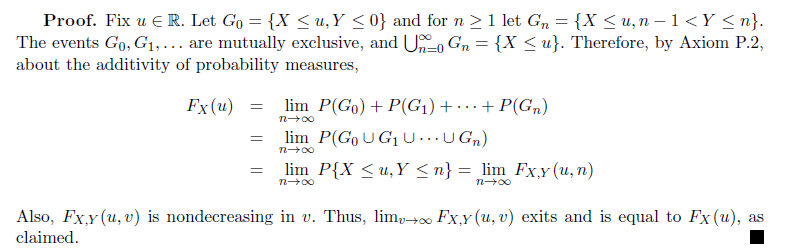
Properties

离散型随机变量 ->Joint Probability Mass Functions
考虑在同一个概率空间中的离散型随机变量 $X,Y$ ,其联合概率质量函数:
$$ P_{X,Y}(u,v) = P(X=u,Y=v) $$
同时结合全概率定理,我们可以由联合概率质量函数导出分别的概率质量函数
$$ P(X=u) =\sum_{j}P(X=u,Y=v_{j}) $$
这等价于
$$ p_{X}(u) =\sum_{j}p_{X,Y}(u,v_{j}) $$
在这种情况下 $p_{X},p_{Y}$ 被称为 联合概率质量函数 $p_{X,Y}$ 的 marginal pmfs,另外 conditional pmfs 由如下 joint pmf 定义:
$$ P_{Y|X}(v|u_{0}) = P(Y=v |X=u_{0}) = \frac{P_{X,Y}(u_{0},v)}{P_{X}(u_{0})} $$
连续型随机变量 -Joint Probability Density Function
对于分布在同一个概率空间中的连续性随机变量 $X,Y$, 其联合概率密度函数 $f_{X,Y}$ 满足 :
$$ F_{X,Y}(u_{0},v_{0}) = \int_{-\infty}^{u_{0}}\int_{-\infty}^{v_{0}}f_{X,Y}(u,v) dudv $$
对于具体区域 $R$ 内,我们有
$$ P{(X,Y)\in R} = \int \int_{R}f_{X,Y}(u,v)dudv $$
Marginal pdfs:
$$
f_{X}(u) = \int_{-\infty}^{\infty}f_{X,Y}(u,v)dv =\int_{-\infty}^{\infty}f_{Y}(v)f_{X|Y}(u|v)du
$$
$$
f_{Y}(v) = \int_{-\infty}^{\infty}f_{X,Y}(u,v)du = \int_{-\infty}^{\infty}f_{X}(u)f_{Y|X}(v|u)du
$$
Conditional pdf:
$$ f_{Y|X}(v|u_{0}) = \frac{f_{X,Y}(u_{0},v)}{f_{X}(u_{0})} $$
$$ E[g(X,Y)] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(u,v)f_{X,Y}(u,v)dudv $$
$$
\begin{align}
& E[X] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}uf_{X,Y}(u,v)dudv
& E[Y] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}vf_{X,Y}(u,v)dudv
\end{align}
$$
同时还有
$$ E[aX+bY+c] = aE[X] + bE[Y]+c $$
$$ E[Y|X=u] = \int_{-\infty}^{\infty}vf_{Y|X}(v|u)dv $$
注意 $E[Y|X=u]$ 可以视为关于 $u$ 的函数,则 $E[Y|X]$ 可以视为关于 $X$ 的函数
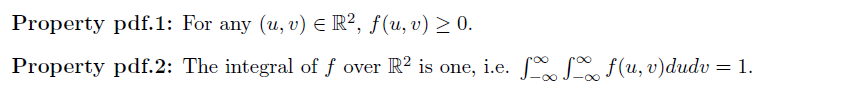


利用 CDF 给出两随机变量独立的条件:
$$ F_{X,Y}(u_{0},v_{0})=F_{X}(u_{0})F_{Y}(v_{0}) $$
在两变量独立的情况下(即满足上式),自然地我们有推论:
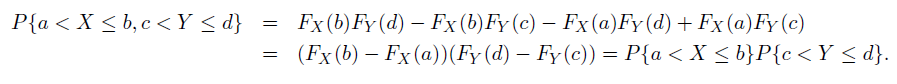
X,Y 相互独立等价于:
$$ f_{X,Y}(u,v)=f_{X}(u)f_{Y}(v) $$
为后续命题先补充相关概念:

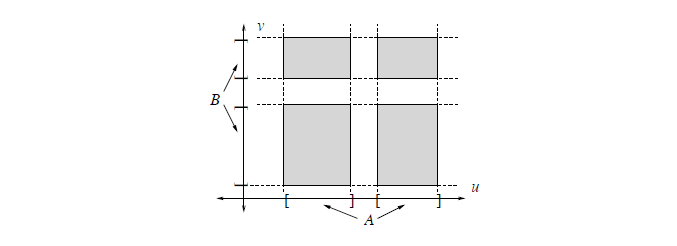
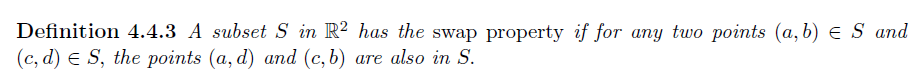
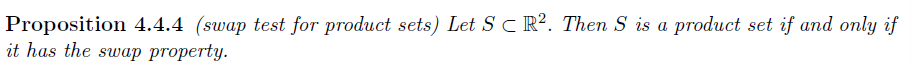
以下两个命题可用来判断自由变量是否随机分布(不一定充要)
Proposition1: 从条件概率角度出发研究变量独立性,考察 conditional pdf 是否仅与单变量有关

Proposition2:X,Y 为相互独立的联合分布连续随机变量,则 $f_{X,Y}$ 支撑集为 product set

推论:当 $X,Y$ 在平面上均匀分布时,其分布集合为 product set 等价于两自由变量随机分布

推导方式:考虑先固定随机变量的和 k,然后对 k 进行遍历
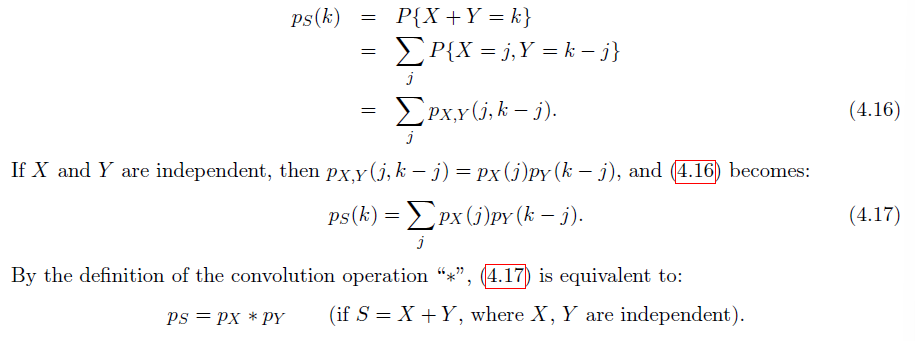
考虑先寻找 $S=X+Y$ 的 CDF 再通过微分得到 PDF
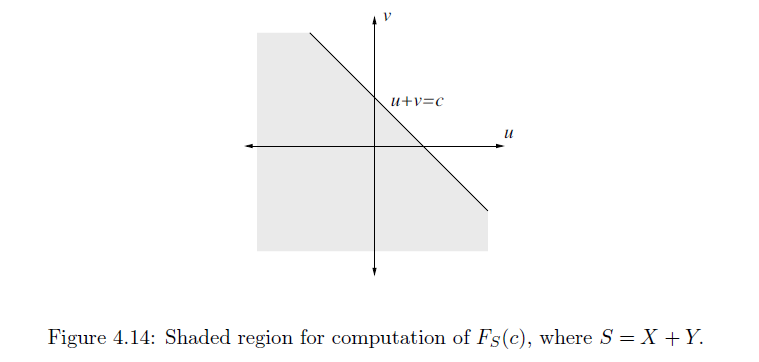
CDF
$$ F_{S}(c) = P(S\leq c) = \int_{-\infty}^{\infty}(\int_{-\infty}^{c-u}f_{X,Y}(u,v)dv)du $$
$$ f_{S}(c) = \frac{dF_{S}(c)}{dc} = \int_{-\infty}^{\infty} \frac{d}{dc}\left( \int_{-\infty}^{c-u}f_{X,Y}(u,v)dv \right)du = \int_{-\infty}^{\infty}f_{X,Y}(u,c-u)du $$
当两者相互独立时(注意 convolution 的记号)
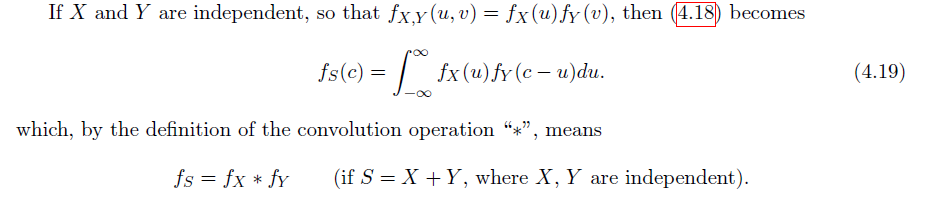
Example: 两满足正态分布的随机变量相加 ->考虑配方

$$ \mu = \mu_{1}+\mu_{2},\ \sigma ^{2}=\sigma_{1}^{2}+\sigma_{2}^{2} $$
Example1: 对圆环范围内积分考虑极坐标换元

Example2:Buffon Needle Problem

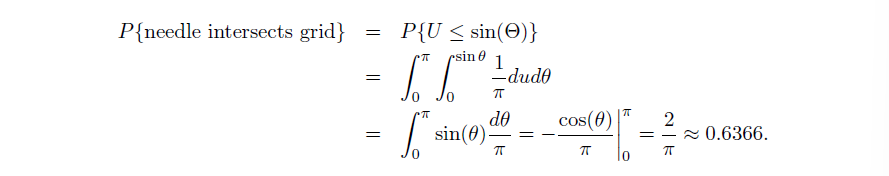
Example4.6.5: ML Estimator,关注如何建模多维联合 pdf,同时进行获得 ML estimator


Example4: max 函数

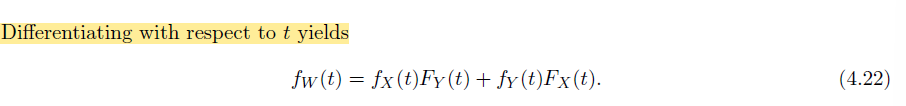
考虑对原有随机变量做线性变换得到新随机变量
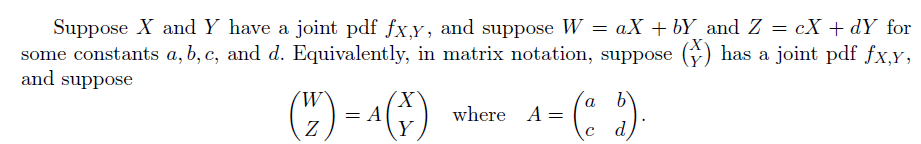
基于线性变换 $A$, 我们可以建立一个由 $u-v$ 平面中的点 $(u,v)$ 经过线性变换得到 $\alpha - \beta$ 中的点 $(\alpha,\beta)$ 的映射
$$
\begin{pmatrix}
\alpha
\beta
\end{pmatrix} = A
\begin{pmatrix}
u
v
\end{pmatrix}, \begin{pmatrix}
u
v
\end{pmatrix} = A^{-1}
\begin{pmatrix}
\alpha
\beta
\end{pmatrix}
$$
记变换前后联合随机变量定义域所对应的区域分别为 $R,S$,则我们有
$$ \text{area}(S) = |\det(A)|\text{area}(R) $$
Proposition
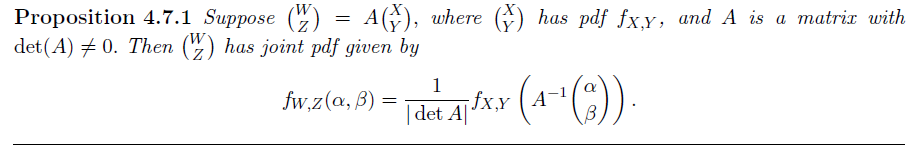
理解:通过除以面积拉伸的系数实现概率密度的对应关系
对于一般的映射 $\begin{pmatrix}W \\ Z\end{pmatrix}=g(\begin{pmatrix}X \\ Y\end{pmatrix})$ ,我们可以利用 Jacobi Matrix 结合线性近似对于特定点附近的情况进行估计
$$
g(\begin{pmatrix}
u
v
\end{pmatrix}) \approx g(\begin{pmatrix}
u_{0}
v_{0}
\end{pmatrix}) + A(\begin{pmatrix}
u
v
\end{pmatrix}-\begin{pmatrix}
u_{0}
v_{0}
\end{pmatrix})
$$
我们可以猜想:
$$ \frac{\text{area}(S)}{\text{area}(R)} \approx|\det(J)| $$
Proposition
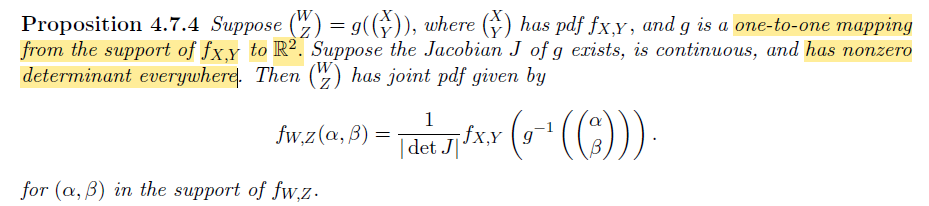
要求:
当定义的函数映射存在多对一的情况是,我们修改命题 4.7.4,将映射后的联合随机变量分布修改为对满足条件的原联合随机变量分布的求和


对于联合随机变量分布,我们考虑类比单随机变量分布的情况引入类似均值与方差的定义
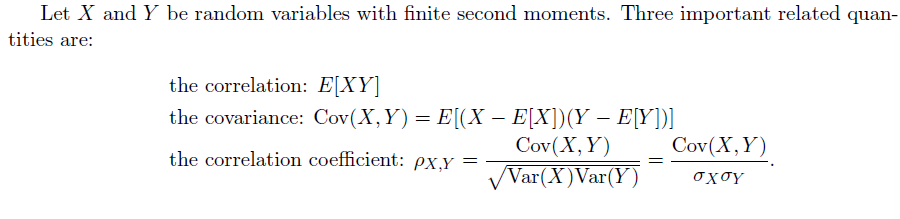
简便计算协方差公式:
$$ \text{Cov}(X,Y) = E[XY]-E[X]E[Y] $$
其中 $E[XY]$ 计算如下:
$$ E[XY] = \int \int uvF_{X,Y}(u,v)dudv $$
协方差&相关:
$$
\begin{align}
& \text{Cov}(X,Y) = 0 (\rho_{X,Y}=0)\to \text{Uncorrelated}
& \text{Cov}(X,Y) > 0 (\rho_{X,Y}>0)\to \text{Positively Correlated}
& \text{Cov}(X,Y) < 0 (\rho_{X,Y}<0)\to \text{Negatively Correlated}
\end{align}
$$
$$ \text{Cov}(X,Y) = E[XY]-E[X]E[Y] = E[X]E[Y]-E[X]E[Y] = 0 $$
$$ \text{Cov}(X,Y) = E[XY] $$
$$ \text{Cov}(X+Y,U+V) =\text{Cov}(X,U)+ \text{Cov}(X,V)+\text{Cov}(Y,U)+\text{Cov}(Y,V) $$
$$ \text{Cov}(aX+b,cY+d) = ac\text{Cov}(X,Y) $$
$$ \text{Var} (X+Y) = \text{Cov}(X+Y,X+Y) = \text{Cov}(X,X)+2\text{Cov}(X,Y)+\text{Cov}(Y,Y) = \text{Var}(X)+\text{Var}(Y) $$
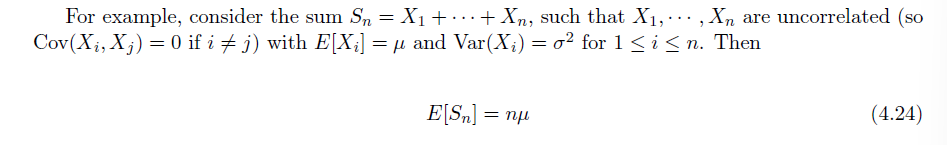

$$ \rho_{aX+b,cY+d} = \rho_{X,Y} \text{ for } a,c >0 $$
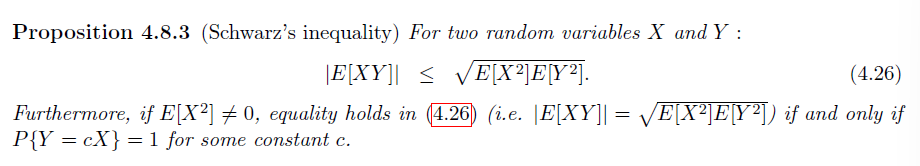
推论:
相关系数的绝对值越接近 1,随机变量的线性相关性越强

注意表示 Sample Mean 与 Sample Variance 时常常用 $\hat{X}$ 或 $\hat{\sigma ^{2}}$

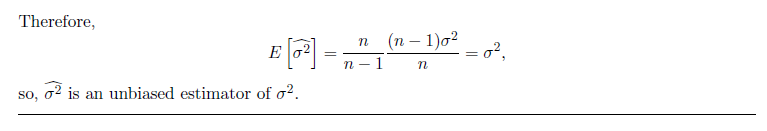
情境建模:
对于一个已知分布随机变量 Y,我们利用一个常数 $\delta$ 去估测 Y 的分布,那么估测误差为 $Y- \delta$ ,我们希望最小化MSE(Mean Square Error)
$$ MSE = E[(y-\delta)^{2}] = \int_{-\infty}^{\infty}(y-\delta)^{2}f_{Y} \, dy $$
经过配方,我们容易将 MSE 化简为与 $\delta$ 有关的二次式
$$ E[(Y-\delta)^{2}] = E[Y^{2}]-2\delta E[Y]+\delta ^{2} $$
当 $\delta = E[Y]$ 时,我们有 MSE 最小值为 $Var(Y)$
即估计的常数对应随机变量分布的均值,相应的 MSE 为其对应的方差
情境建模:
希望基于随机变量 $Y$ 的观测结果 $X$ 估计 $Y$ ,我们考虑确定一个估计函数 $g(X)$ 对 Y 进行估计 ,最小化 MSE $E[Y-g(X)]^{2}$ . 最终求得的估计值 $g^{*}(X)$ 被称为 unconstrained optimal estimator
Example

注意利用条件概率公式化简(固定某一个 u,符合我们在确定观测 X 的情况下估计 Y)
[!tip] 结论
对于非限制在给定观测结果 $X$ 的情况下估计随机变量 $Y$ 的分布,我们基于常数估计量以及 conditional pdf 推导出
$E[Y X]=g^{}(X)$ 其中 $g^{}(u)=E[Y X=u]$
对应的 MSE 最小值为 $E[(Y-E[Y X])^{2}]=E[Y^{2}]-E[(E[Y X])^{2}]$ 先根据联合概率分布 $f_{X,Y}$ 计算 $f_{X}$ 与 $f_{Y|X}$
再对每一个给定的 $u$ ,确定 $g^{*}(u)$ , 即利用积分计算条件期望
然后计算每一个给定的 u 对应的 MSE 再乘上相对应的 $f_{X}(u)$ ,积分得到最终结果
情境建模
考虑将用观测结果 $X$ 去线性估计随机变量 $Y$, 我们只需确定使 MSE 最小的 Linear Estimator $L(X)=aX+b$
此时 MSE 为:
$$ MSE = E[(Y-(aX+b))^{2}] $$
我们可以考虑采取分别求偏导或者累次优化的方式寻找 MSE 最小时对应的 $a,b$ 值

根据逐步优化的结果,我们有给 $Y$ 的线性近似 $aX+b$
当
$$ a = \frac{\text{Cov}(Y,X)}{\text{Var}(X)}, b = \mu_{Y}-a\mu_{X} $$
时,我们有 MSE 最小,此时
$$
\begin{align}
& L(X) = \hat{E}[Y|X] = \mu_{Y}+ \frac{\text{Cov}(Y,X)}{\text{Var}(X)}(X-\mu_{X}) = \mu_{Y} + \sigma_{Y}\rho_{X,Y} \left( \frac{X-\mu_{X}}{\sigma_{X}} \right)
& MSE = \sigma_{Y}^{2}-\frac{(\text{Cov}(X,Y))^{2}}{\text{Var}(X)} = \sigma_{Y}^{2}(1-\rho ^{2}_{X,Y}) = E[Y^{2}] - E[\hat{E}[Y|X]^{2}]
\end{align}
$$
其中使得 MSE 最小的线性估计 $\hat{E}[Y|X]$ 又被称为 wide sense conditional expectation(广义条件期望)
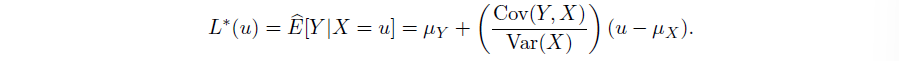
我们发现当 X,Y 线性相关程度越高(即 $\rho_{X,Y}$ 绝对值越接近 1)时,用线性估计 Y 的 MSE 越小 ->体现了相关系数对两自由变量线性相关的衡量
三种方法估计的比较 ->假设越宽泛,优化得到的 MSE 越小
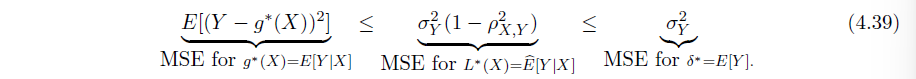
重点关注 Example 4.9.2
LLN 建模基于的情境:
给定一系列均值相同的独立(或弱相关的)的随机变量,同时对随机变量的规模有一定要求,LLN 认为当随机变量个数趋于无穷时,他们和的均值收敛于一个定值
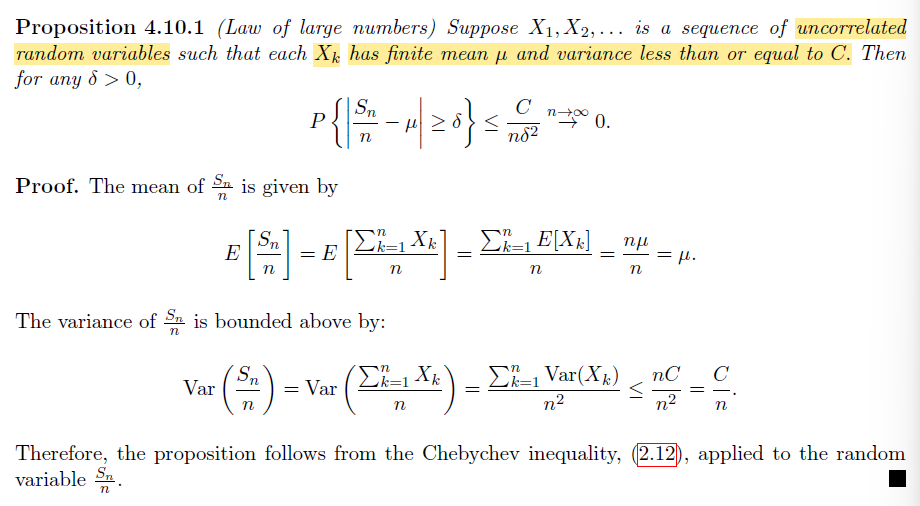
关注例题 4.10.4

中心极限定理:
认为多个独立相同分布的随机变量(均值与方差均有限),他们和的分布标准化后趋于高斯分布
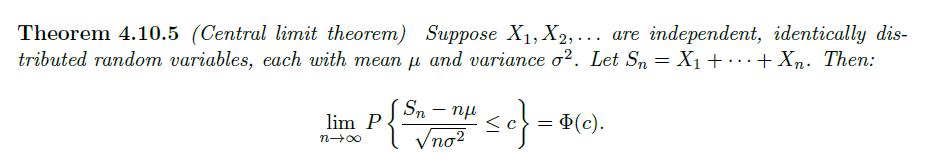
注意有时需要对高斯近似用 Continuity Correction
联合高斯分布随机变量 ->对于这些随机变量的线性组合满足高斯分布


判别两变量是否符合高斯联合随机分布的另一种方法 ->研究其 pdf 是否为关于两变量的符合条件的指数上二次多项式 (bivariate normal pdf)(非退化的情况)

先研究标准双变量正态分布的情况 ->再通过线性变换(变换方差与相关系数)以及平移(改变均值)得到一般形式

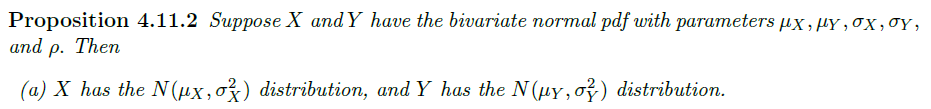
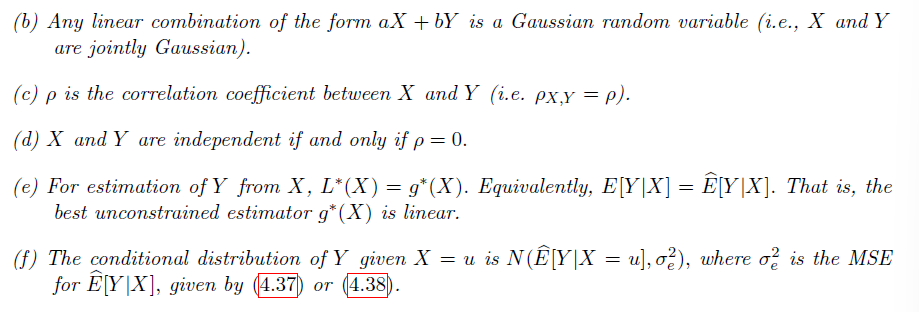
注意
| **给定 X 关于 Y 的分布为条件概率分布为正态分布 $N(\hat{E}[Y | X=u],\sigma_{e}^{2})$**,注意与上述 Linear Estimator 相关联(见 Homework13 5) |
性质的证明



