#ECE210

Operational amplifiers and signal arithmetic

运算放大器的基本结构

输入： $v_{+},v_{-}$,其中 $v_{+}$ 为 noninverting input terminal, $v_{-}$ 为 inverting input terminal
输出： $v_{o}$
输入与输出的关系如下：

$$ v_{o} = A(v_{+}-v_{-}) - R_{o}i_{o} $$

输入与输出电阻： $R_{i},R_{o}$
电压增益系数： $A$
典型参数的大致数量级：

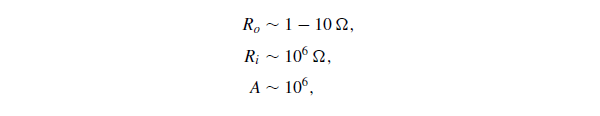
op-amp 的线性状态与饱和状态

输出电压 $v_{o}$ 具有饱和值 $v_{b}$ ,当 $ v_{+}-v_{-} < \frac{v_{b}}{A}$ 时 $v_{o}$ 与输入的差分成线性
当 $|v_{+}-v_{-}|> \frac{v_{b}}{A}$ , $v_{o}$ 达到饱和
为了满足线性状态，我们需要输入的差分非常小，在实际情况下近似为
注意电路分析时这可作为 op-amp 的隐藏条件

Voltage follower and noninverting amplifier

Voltage Follower 电压跟随器

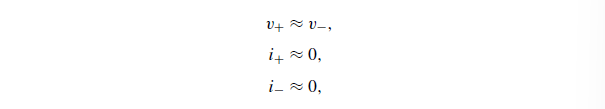
Voltage Follower（电压跟随器），又称 单位增益缓冲器（Unity Gain Buffer），是一种特殊的 运算放大器（Op-Amp） 电路。其 输出电压等于输入电压（Vout = Vin），但它具有 高输入阻抗、低输出阻抗，主要用于信号隔离、阻抗匹配和信号缓冲。

1. 主要作用
在连接两个电路时，我们希望两个电路能够分别独立工作不相互影响，此时 Voltage Follower 能够保证输入电压与输出端子的电压相同，可以作为缓冲器

电压增益： $A_{v} = 1$
与输入信号同相
输入阻抗高，输出阻抗低

2. 工作原理 ->负反馈
通过将输出端子的电压接回输入反向电压，只要 $|v_{s}<v_{b}|$ 我们能够一直将 $v_{o}$ 控制在线性范围内

3. 注意事项
如果我们将输出端子连接到正向输入电压，则我们无法保证 op-amp 在线性工作范围内

Noninverting Amplifier 非反向放大器

Non-Inverting Amplifier（非反相放大器）是一种 运算放大器（Op-Amp） 放大电路，能够 放大输入信号，而不会改变信号的相位（即输入与输出同相）。它的电压增益由外部反馈电阻网络决定，通常大于 1。

1. 主要特点：

放大输入信号
输出信号与输入信号同相。
高输入阻抗，几乎不影响前级信号源。
低输出阻抗，能够驱动负载。

2. 工作原理
通过改变输出端负载电阻的结构 + 负反馈对输出电压进行放大

根据电路分析我们有:

$$ v_{s} = v_{o} \frac{R_{2}}{R_{1}+R_{2}} $$

进一步我们有增益系数：

$$ A = \frac{R_{1}}{R_{2}} +1 $$

Inverting Amplifier 反相放大器

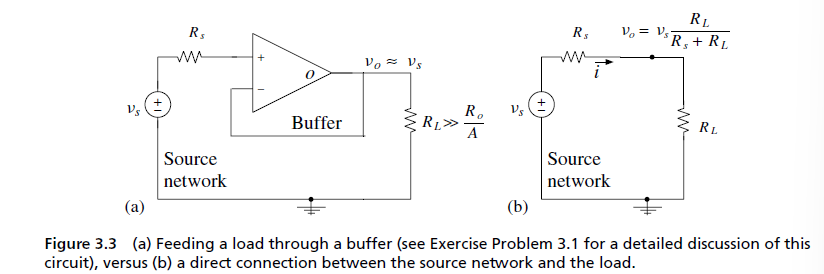
反相放大器（Inverting Amplifier） 是一种 运算放大器（Op-Amp） 电路，能够 放大输入信号，同时使输出信号相位相反（倒置 180°）。其电压增益由外部电阻决定，通常为 负值（即输出信号倒置）。

1. 主要特点

放大输入信号（可控增益）
输出信号与输入信号反相（相差 180°）
低输入阻抗，适合低阻抗信号源
负反馈稳定，线性放大
可用于求和放大器（Summing Amplifier）、积分电路等

2. 工作原理

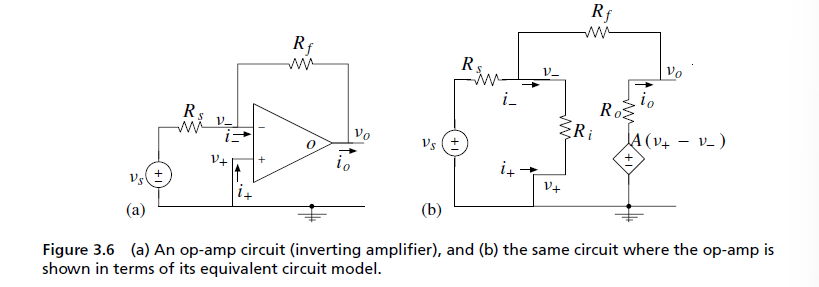
$$ \begin{align} & v_{o} \approx -\frac{R_{f}}{R_{s}} v_{s}
& G = \frac{v_{o}}{v_{s}} \approx - \frac{R_{f}}{R_{s}} \end{align} $$

Sums and Differences

Sum circuit

工作原理

Difference circuit

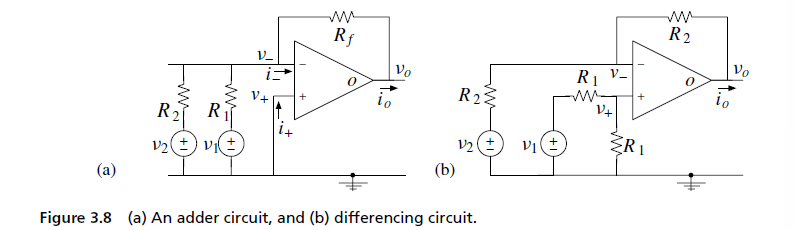
工作原理
注意到：

$$ v_{-} \approx v_{+} \approx \frac{v_{1}}{2} $$

进而我们有

$$ \begin{align} & \frac{v_{2}-\frac{1}{2}v_{1}}{R_{2}} \approx \frac{\frac{1}{2}v_{1}-v_{o}}{R_{2}}
& v_{o} \approx v_{1} - v_{2} \end{align} $$

Differentiators and Integrators

Differentiator Circuits 微分电路

Capacitors and Inductors as differentiators
电容与电感作为微分器 ->考虑其在交变电路中核心特性

$$ \begin{align} & i = C \frac{dv}{dt}
& v = L \frac{di}{dt} \end{align} $$

1. 工作原理

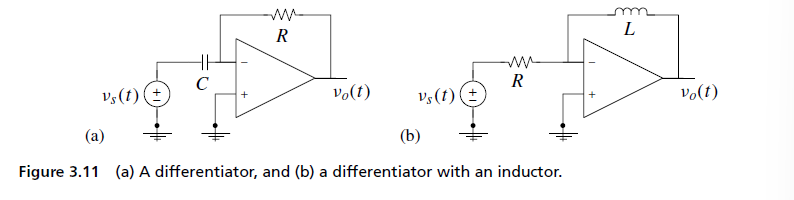
$$ \begin{align} & - \frac{v_{o}(t)}{R} = C \frac{d}{dt} (v_{s}(t)-0) = C \frac{dv_{s}}{dt}
& v_{o} (t) = -RC \frac{dv_{s}}{dt} \end{align} $$

对于电感电路，则有

$$ v_{o}(t) = -\frac{L}{R} \frac{dv_{s}}{dt} $$

Integrator Circuits

Capacitors and Inductors as integrators
电容电感作为积分器：

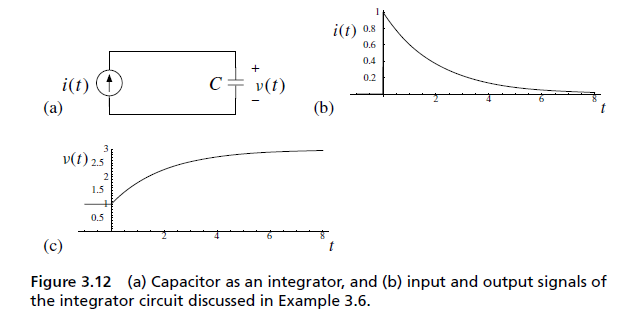
注意：

由输入电流在电容上的反应电压一定是连续的

$$ \int_{a}^{b}i(t)dt = \int_{a}^{b}C \frac{dv}{dt} dt = C \int_{a} ^{b}dv = C[v(b)-v(a)] $$

由输入电压作用在电感上的反应电流一定是连续的

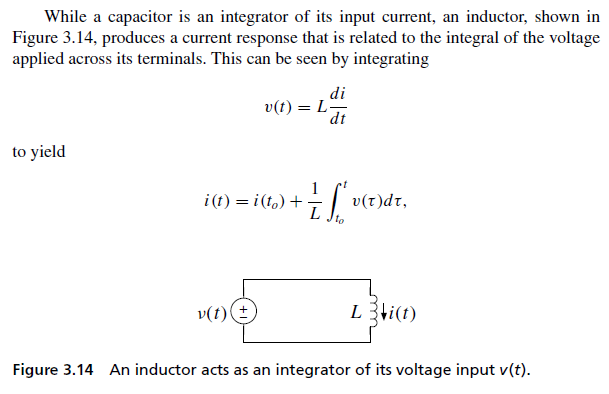
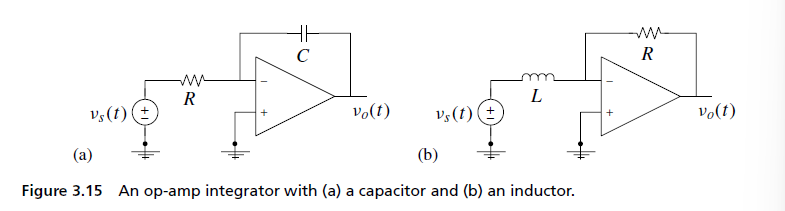
Op-amp Integrators

Linearity, Time Invariance and LTI Systems

Response Summary

特性	Zero-State Response (零状态响应)	Zero-Input Response (零输入响应)	Transient Response (瞬态响应)	Steady-State Response (稳态响应)
定义	系统仅由输入（激励）引起的响应，初始状态为零。	系统仅由初始状态（初始条件）引起的响应，输入为零。	系统响应中随时间衰减的部分，最终消失。	系统响应中随时间保持不变或周期性变化的部分，是响应的最终行为。
产生原因	外部输入信号 (例如阶跃信号、正弦信号)	初始储能元件的状态 (例如电容的初始电压、电感的初始电流)	系统能量的耗散（如电阻中的损耗）和储能元件的充电/放电。	输入信号的特性以及系统本身的特性。
初始状态	零 (所有初始条件为零)	非零 (存在初始条件)	取决于具体的系统和输入/初始状态。	取决于具体的系统和输入。
输入信号	存在	零 (没有外部输入)	存在 (一般)	存在 (一般)
时间特性	通常包含瞬态和稳态成分。	随时间衰减至零 (对于稳定系统)。	随时间衰减至零 (对于稳定系统)。	随时间保持不变或周期性变化。
包含成分	仅包含由输入引起的响应。	仅包含由初始状态引起的响应。	包含由输入和/或初始状态引起的，且随时间衰减的成分。	包含由输入和/或初始状态引起的，且随时间保持不变或周期性变化的成分。
计算方法	通常使用卷积积分、传递函数等方法。	通常求解齐次微分方程，并根据初始条件确定解。	需要求解系统的完整微分方程或使用拉普拉斯变换等方法得到时域表达式，然后观察其瞬态特性。	可以使用传递函数或直接分析系统在长时间后的行为来确定。
叠加关系	总响应 = Zero-State Response + Zero-Input Response (线性系统适用)	不适用 (Zero-Input Response 本身就是没有输入的响应)	总响应 = Transient Response + Steady-State Response (线性系统适用)	不适用 (Steady-State Response 是响应的稳定部分)
举例	一个 RLC 串联电路，初始状态为 0，输入一个阶跃电压，电路中的电流就是 Zero-State Response	一个 RLC 串联电路，没有外部电压源，但是电容上有一个初始电压，电路中的电流就是 Zero-Input Response	一个 RLC 串联电路，输入一个阶跃电压，电路中的电流的变化过程中的振荡衰减的部分就是 Transient Response	一个 RLC 串联电路，输入一个正弦电压，电路中的电流经过一段时间后稳定的正弦变化部分就是 Steady-State Response

关键要点：

Zero-State vs. Zero-Input: 这两个概念将系统的总响应分解为由输入引起的响应和由初始状态引起的响应。它们是叠加原理的基础，只适用于线性系统。
Transient vs. Steady-State: 这两个概念将系统的总响应分解为随时间衰减的部分和最终的稳定部分。它们关注的是响应在时间上的行为。
关系: 总响应可以表示为：
- 总响应 = Zero-State Response + Zero-Input Response (线性系统)
- 总响应 = Transient Response + Steady-State Response (线性系统)

线性（Linearity）

线性是系统的一个关键属性，它由两个子属性构成：叠加性（Additivity）和齐次性（Homogeneity）。一个系统被称为线性，当且仅当它同时满足这两个性质。

叠加性（Additivity）： 叠加性意味着，如果我们将两个输入信号分别通过系统，然后将它们的输出相加，结果与将这两个输入信号先相加再通过系统得到的结果相同。

数学公式：

$$ \text{如果 } x_1(t) \rightarrow y_1(t) \text{ 且 } x_2(t) \rightarrow y_2(t)，\text{ 那么 } x_1(t) + x_2(t) \rightarrow y_1(t) + y_2(t)

$$ 这意味着系统对多个输入信号的响应是每个信号单独响应的简单叠加。

齐次性（Homogeneity）/ 比例性（Scaling）： 齐次性意味着，如果我们将输入信号乘以一个常数，那么输出信号也会乘以相同的常数。

数学公式：

\text{如果 } x(t) \rightarrow y(t)，\text{ 那么 } a \cdot x(t) \rightarrow a \cdot y(t)

$$ 这里，$a$ 是一个复数标量。这表明系统的响应与输入信号的幅度成比例。

注意分别检验

Zero-state response：单独考虑外部输入信号引发的信号相应，不考虑初始状态对系统的影响
Zero-input response：没有外部输入（电压为0）的情况下，由于系统的初始条件（如电容的初始电荷，电感的初始电流）引起的电压相应。

时不变性（Time Invariance）

时不变性是指系统的特性不随时间变化。换句话说，无论何时将相同的输入信号应用于系统，都将得到相同的输出信号（只是可能在时间上有所平移）。

数学公式： $$

\text{如果 } x(t) \rightarrow y(t)，\text{ 那么 } x(t - t_0) \rightarrow y(t - t_0)

$$ 这意味着如果将输入信号延迟 $t_0$，那么输出信号也会延迟相同的 $t_0$，而输出信号的形状和幅度不会发生改变。

线性时不变系统（LTI Systems）

线性时不变系统（Linear Time-Invariant Systems，简称 LTI 系统）是同时满足线性和时不变性的系统。 LTI 系统是信号处理和系统分析中的基石，因为它们具有以下重要特性：

完全由单位脉冲响应描述： LTI 系统的行为完全由其单位脉冲响应（Impulse Response）$h(t)$ 描述。单位脉冲响应是系统对单位脉冲信号 $\delta(t)$ 的响应。
卷积性质： LTI 系统的输出 $y(t)$ 可以通过输入信号 $x(t)$ 和系统的单位脉冲响应 $h(t)$ 的卷积计算得到。

数学公式：

y(t) = x(t) * h(t) = \int_{-\infty}^{\infty} x(\tau) h(t - \tau) d\tau

$$ 这个卷积积分表明，输出信号是输入信号在所有时间点上与单位脉冲响应的加权平均。

频域分析： LTI 系统的频域分析非常简单。如果 $X(f)$ 是输入信号 $x(t)$ 的傅里叶变换，$H(f)$ 是单位脉冲响应 $h(t)$ 的傅里叶变换（也称为频率响应），那么输出信号 $y(t)$ 的傅里叶变换 $Y(f)$ 就是 $X(f)$ 和 $H(f)$ 的乘积。

数学公式： $$

Y(f) = X(f) \cdot H(f)

$$ 这意味着 LTI 系统对不同频率成分的影响可以通过其频率响应 $H(f)$ 来分析。

First-Order RC and RL circuits

RC,RL Circuits response to constant sources

一阶 RC 和 RL 电路是最基本的时域电路，它们包含一个电阻器（R）和一个电容器（C）或一个电阻器（R）和一个电感器（L）。这些电路的响应是指数衰减或增长，因此被称为“一阶”电路。

RC 电路

电路构成： RC 电路由一个电阻器（R）和一个电容器（C）串联组成，并连接到一个电压源或电流源。
分析方法： 分析 RC 电路通常使用基尔霍夫电压定律（KVL）或基尔霍夫电流定律（KCL），并结合电容器的 i-v 关系：$i_C(t) = C \frac{dv_C(t)}{dt}$。
微分方程： RC 电路的电压 $v_C(t)$ 的变化可以用以下一阶线性微分方程描述：

RC \frac{dv_C(t)}{dt} + v_C(t) = v_S(t)

$$ 其中，$v_S(t)$ 是电压源的电压。如果电路是由电流源驱动，方程式将是电流的微分方程。

自然响应（Natural Response）： 当没有外部电源时（$v_S(t) = 0$），电路的响应称为自然响应。电压 $v_C(t)$ 的自然响应形式为： $$

v_C(t) = V_0 e^{-t/RC}

$$ 其中，$V_0$ 是电容器的初始电压，$RC$ 是时间常数（time constant），表示电压衰减到其初始值的 $1/e$ (约 36.8%) 所需的时间。

阶跃响应（Step Response）： 阶跃响应是指当输入电压 $v_S(t)$ 是一个阶跃函数 $V_s u(t)$ 时，电路的响应。其中 $u(t)$ 是单位阶跃函数，当 t < 0 时 u(t)=0, 当 t >= 0 时 u(t) = 1。电压 $v_C(t)$ 的阶跃响应形式为： $$

v_C(t) = (V_{0}-V_{s})e^{-\frac{t}{RC} } +V_{s}

$$ 其中，$V_s$ 是阶跃电压的幅度，$V_0$ 是电容器的初始电压。当 $t \to \infty$ 时，$v_C(t)$ 趋近于 $V_s$。 即对应电容器具有初始电压 $V_{0}$ ,接入外部电压 $V_{s}$ 后的充放电情况

时间常数： 时间常数 $\tau = RC$ 是 RC 电路的重要参数。它表示电容器充电或放电的速度。时间常数越大，充电或放电过程越慢。

RL 电路

电路构成： RL 电路由一个电阻器（R）和一个电感器（L）串联组成，并连接到一个电压源或电流源。
分析方法： 分析 RL 电路通常使用基尔霍夫电压定律（KVL）或基尔霍夫电流定律（KCL），并结合电感器的 i-v 关系：$v_L(t) = L \frac{di_L(t)}{dt}$。
微分方程： RL 电路的电流 $i_L(t)$ 的变化可以用以下一阶线性微分方程描述： $$

L \frac{di_L(t)}{dt} + Ri_L(t) = v_S(t)

$$ 其中，$v_S(t)$ 是电压源的电压。

自然响应（Natural Response）： 当没有外部电源时（$v_S(t) = 0$），电路的响应称为自然响应。电流 $i_L(t)$ 的自然响应形式为： $$

i_L(t) = I_0 e^{-Rt/L}

$$ 其中，$I_0$ 是电感器的初始电流，$L/R$ 是时间常数。

阶跃响应（Step Response）： 阶跃响应是指当输入电压 $v_S(t)$ 是一个阶跃函数 $V_s u(t)$ 时，电路的响应。电流 $i_L(t)$ 的阶跃响应形式为： $$

i_L(t) = \frac{V_s}{R} (1 - e^{-Rt/L}) + I_0 e^{-Rt/L} = [I_{0}-I_{s}]e^{- \frac{t}{\tau}} +I_{s}

$$ 其中，$V_s$ 是阶跃电压的幅度，$I_0$ 是电感器的初始电流。当 $t \to \infty$ 时，$i_L(t)$ 趋近于 $V_s/R$。

时间常数： 时间常数 $\tau = L/R$ 是 RL 电路的重要参数。它表示电感器中电流增长或衰减的速度。时间常数越大，电流变化过程越慢。

RC, RL-circuit response to time-varying sources

一般的 RC, RL 关于时变源的电路可以泛化为以下的一阶线性常微分方程 $$

\frac{dy}{dt} +ay(t) = b f(t)

$$ 对于该 ODE，我们只需确定 initial condition 及其对应的特解 + 齐次解即可解决

解的基本形式： $$

y(t) = Ae^{-at} + y_{p}(t)

$$ 结合初始条件我们有： $$

y(t) = [y(0)-y_{p}(0)]e^{-at}+y_{p}(t)

常见的特解形式：

Steady State Response (稳态响应) vs. Transient Response (瞬态响应)

1. Transient Response (瞬态响应)

定义: Transient response 是系统从初始状态过渡到稳态状态过程中所表现出的响应。它描述了系统在受到输入激励后，暂时性的、不稳定的行为。
特性:
- 随时间衰减: Transient response 通常包含随时间衰减的成分。这些成分可能是指数衰减、振荡衰减等。
- 与系统动态特性相关: Transient response 的形状和持续时间直接反映了系统的动态特性，如阻尼、自然频率等。
- 关注点： 主要关注响应的速度（上升时间、建立时间）、超调量（最大峰值超出稳态值的程度）和振荡情况。

2. Steady State Response (稳态响应)

定义: Steady state response 是系统在足够长的时间后，达到的一种稳定、持续的响应状态。此时，系统的输出不再随时间发生显著变化（或呈现周期性变化）。
特性:
- 与输入信号相关: 稳态响应的形状和幅度通常与输入信号密切相关。例如，对于阶跃输入，稳态响应可能是一个常数值；对于正弦输入，稳态响应可能是一个具有相同频率的正弦信号。
- 与系统静态特性相关: 稳态响应的幅值和相位反映了系统的静态特性，如增益、相位裕度等。
- 关注点： 主要关注响应的准确性（稳态误差）、稳定性和周期性。

关系与区别：

特性	Transient Response (瞬态响应)	Steady State Response (稳态响应)
时间段	短时间，系统刚开始响应的阶段	长时间，系统稳定后的阶段
行为	不稳定，随时间衰减或振荡	稳定，持续的
影响因素	系统自身的动态特性（如阻尼、自然频率）	输入信号和系统的静态特性（如增益）
关注指标	上升时间、建立时间、超调量、阻尼比	稳态误差、稳定性、周期性
描述	系统如何从初始状态过渡到稳态状态	系统最终稳定后的行为

nth-Order LTI Systems

我们可以用 n 阶微分方程来描述带有 n 个独立能量储存元件的线性电路

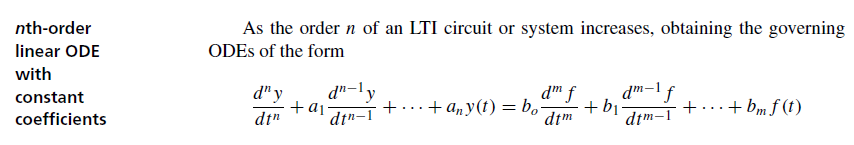
对于 zero-input state solution,我们考虑构造任意 n 阶齐次线性微分方程的解 ->直接利用特征根方程